On this page, we'll look at how we can use integration to find areas. This is a really common question in examinations. The technique is not too hard, but there are just a couple of pitfalls to avoid which will be explained. There are 3 cases that we will consider here, the area between:
- a graph and the x axis
- a graph and the y axis
- two graphs
On this page, you should learn about
- area of a region enclosed by a curve and the x axis
- area of a region enclosed by a curve and the y axis
- area between two graphs
Here are all the different cases that you need to know about
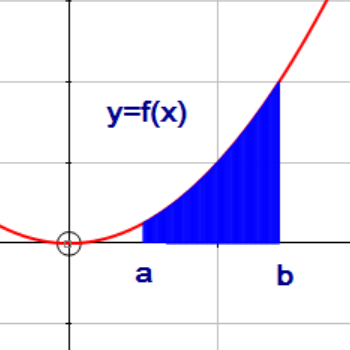
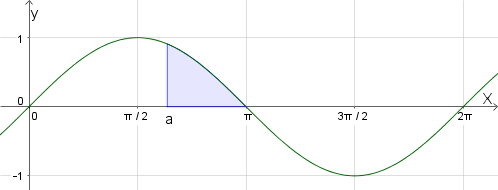
The area between the curve y=f(x) and the x axis can be found using the formula
\(\int _{ a }^{ b }{ y } \ dx\)
or using function notation:
\(\int _{ a }^{ b }{ f(x) } \ dx\)
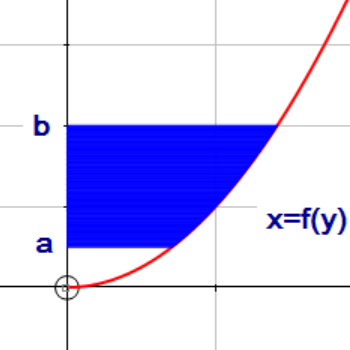
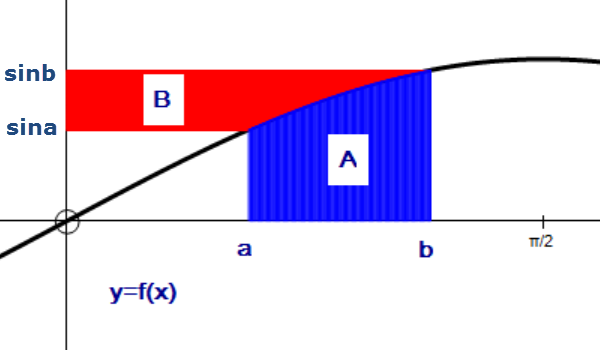
The area between the curve x=f(y) and the y axis can be found using the formula
\(\int _{ a }^{ b }{ x } \ dy\)
or using function notation:
\(\int _{ a }^{ b }{ f(y) } \ dy\)
We should always draw a sketch of the graph before we calculate the area since any part below the axis will be calculated as a negative value. Below, we consider the area between the graph y = x²-1 and the x axis. You can check these definite integrals with your GDC:
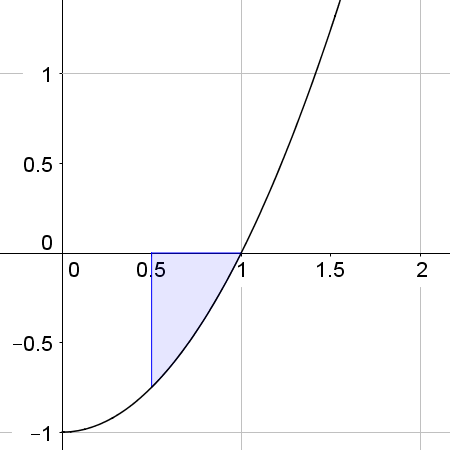 |  | 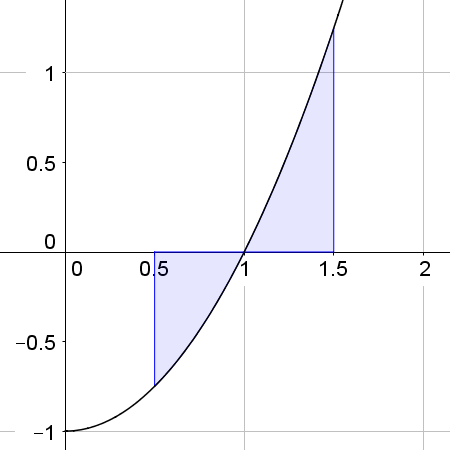 |
| \(\int _{ 0.5}^{ 1 }{ x^2 } \ dx \approx -0.21\) The area \(\approx 0.21\) | \(\int _{ 1}^{ 1.5 }{ x^2 } \ dx \approx 0.29\) The area \(\approx 0.29\) | \(\int _{ 0.5}^{ 1.5}{ x^2 } \ dx \approx 0.083\) The area is NOT equal to 0.083 |
Clearly, the area of the third graph is NOT 0.083 and CANNOT be found by evaluating \(\int _{ 0.5}^{ 1.5}{ x^2 } \ dx\)
The area \(\approx 0.21+0.29\approx 0.50\)
There are different ways of finding the area is this case. The simplest is to evaluate separately the part that is above to the part that is below the axis. We then make the part below a positive value.
In this case,
area = \(|\int _{ 0.5}^{ 1}{ x^2 } \ dx|\quad+\quad\int _{ 1}^{ 1.5}{ x^2 } \ dx\)
In General
 The area between the curve y=f(x) and the x axis can be found using the formula
The area between the curve y=f(x) and the x axis can be found using the formula
\(|\int _{ a}^{ b}{ y } \ dx|\quad+\quad|\int _{ b}^{ c}{ y } \ dx|\)
We can use function notation
\(|\int _{ a}^{ b}{ f(x) } \ dx|\quad+\quad|\int _{ b}^{ c}{ f(x) } \ dx|\)
You will need to find the zeros (y intercepts) of your graph.
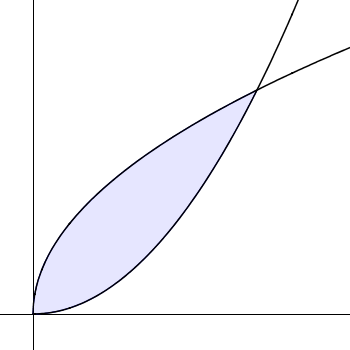
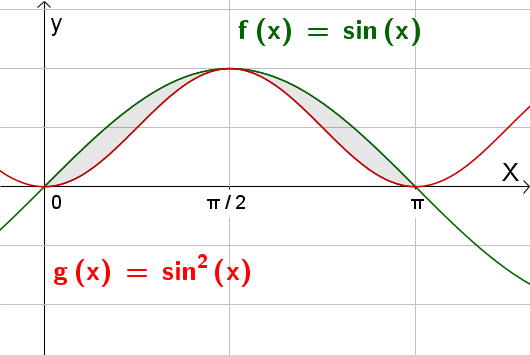
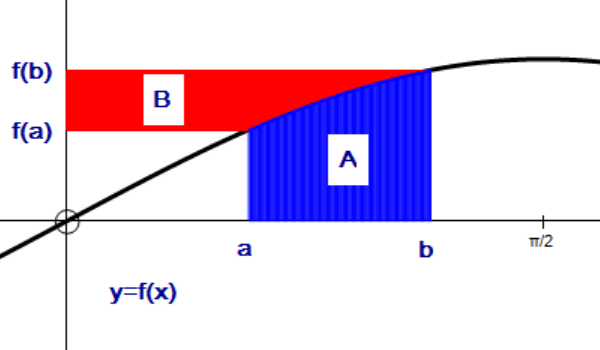
To find the area bounded by two graphs like this, we need to subtract one area from the other:
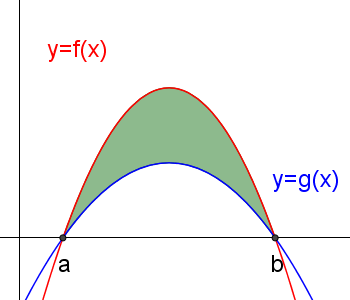 equals
equals  subtract
subtract 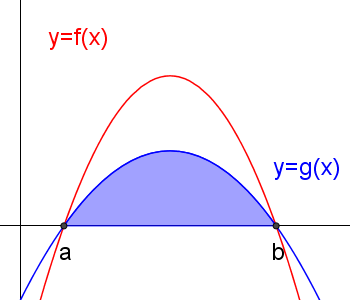
\(\int _{ a }^{ b }{ f(x) } \ dx\quad-\quad \int _{ a }^{ b }{ g(x) } \ dx\)
In this case, you do not have to worry about graph being above or below the x axis!
Here are video examples to help you understand the concepts from this page
Print from here
How much of Area between Graphs HL have you understood?


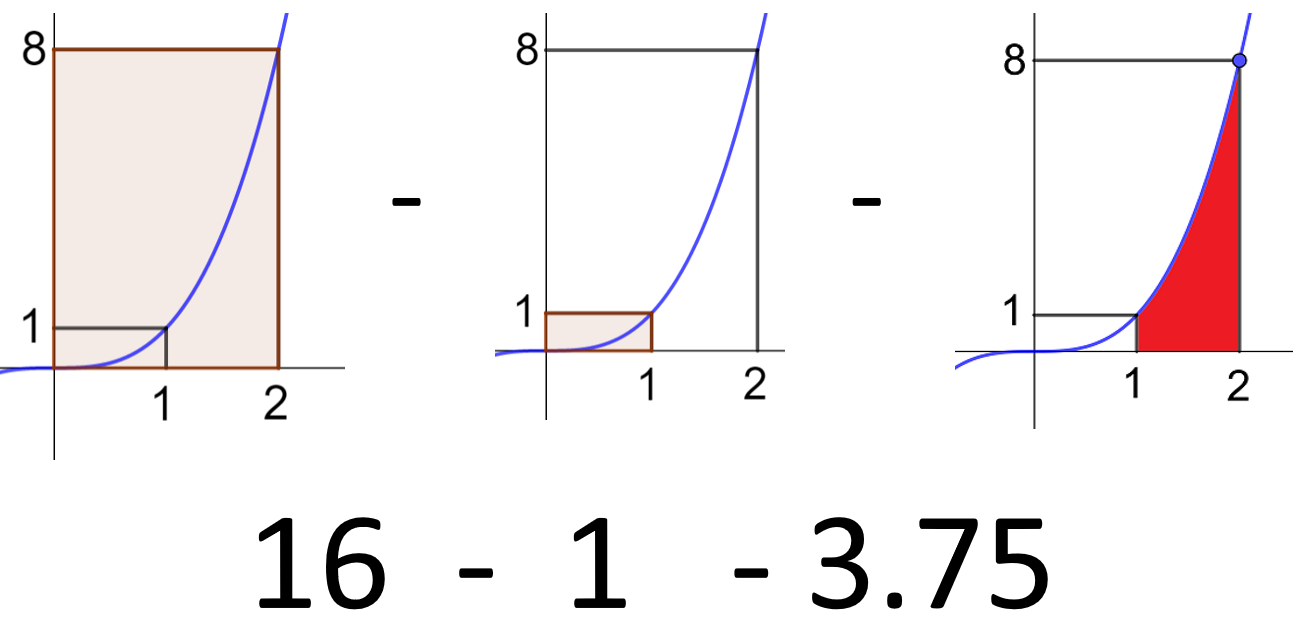
 Find the area of the region bounded by the graph
Find the area of the region bounded by the graph 

 integration of lnx
integration of lnx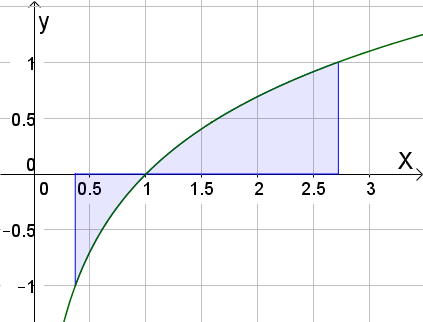





 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn