

There are many practical applications of differentiation that you will meet in your IB subjects and later in your professional career
- acceleration = rate of change of velocity
- population growth = rate of population
- force applied to a body = rate of change of momentum
- marginal cost = rate of change of cost
- chemical reaction rate = rate of change of concentration
On this page, you should learn about
- rates of change
- gradient function
- differentiation from first principles
- different notation for derivatives
- the power rule to differentiate \(ax^n\)
The following videos will help you understand all the concepts from this page
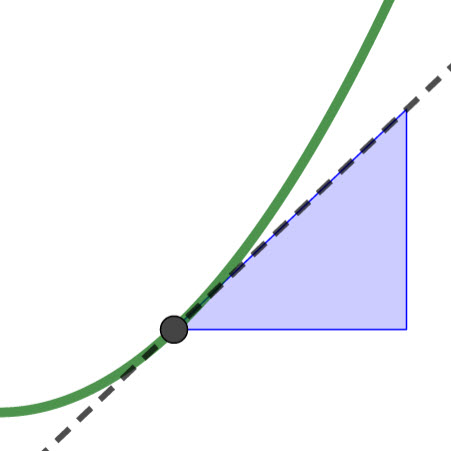
The graph of the function f(x) = x² is shown below.
This applet calculates an approximation of the gradient of f(x) at A. You should notice that the secant AB is steeper than the gradient of the graph at A. However, you can improve the approximation by dragging the point B closer to A. The closer the point B moves to A, the better and better the approximation becomes. Try it for yourself!
This is the basis of where the definition of the gradient function comes from.
The graph below shows the general function f(x) = \(x^n\)
As before, the secant gives an approximation of the gradient of the curve.
As the two points get closer and closer, the approximation gets better and better.
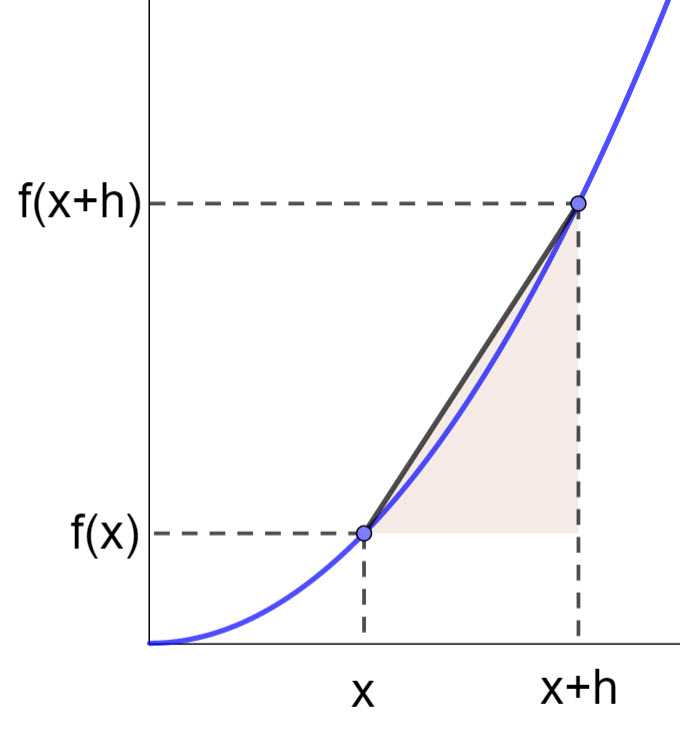
If we could make this secant infinitesimally small, then the gradient of the secant would equal the gradient of the curve at this point.
The limit of the gradient of an infinitesimally small secant gives the gradient of the curve. We can describe this using the following formula
\(f'(x)=\lim\limits_{h \to 0} \frac{f(x+h)-f(x)}{h}\)
The process of finding the gradient function like this is sometimes called differentiation from first principles. In the following video, we will look at using this formula to find the gradient function for f(x) = x²
Notes from the video
Print from here
The Power Rule for differentiating functions in the form f(x) = axn is not difficult to use. Often the tricky thing is to understand the indices in the function. This quiz gives you some practice in manipulating indices. Fill in the gaps
START QUIZ!
The following quiz gives you some practice in using the Power Rule
START QUIZ!
How much of Introducing Derivatives have you understood?






 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn