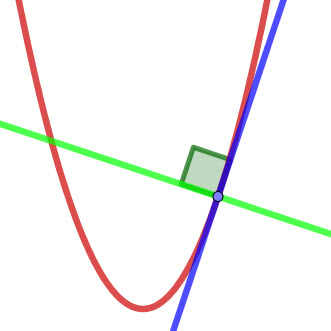
 On this page we look at how to find the equation of a tangent and also the normal to a curve. A tangent is a straight line that touches a curve at one point and has the same gradient as the curve at that point. A normal is straight line that is perpendicular to the tangent to the curve. We use the gradient function and need to know a point on the line.
On this page we look at how to find the equation of a tangent and also the normal to a curve. A tangent is a straight line that touches a curve at one point and has the same gradient as the curve at that point. A normal is straight line that is perpendicular to the tangent to the curve. We use the gradient function and need to know a point on the line.
On this page, you should learn about
- equations of a tangent to a curve at a given point
- equations of a normal to a curve at a given point
The following videos will help you understand all the concepts from this page
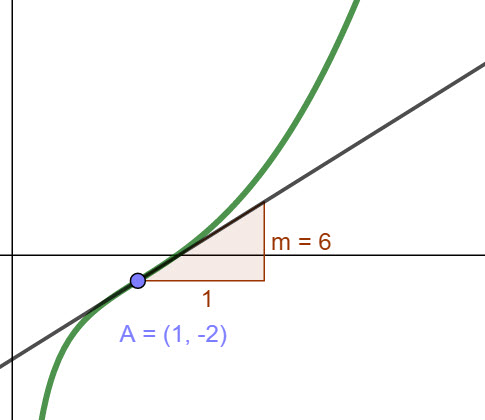
A tangent is a straight line that touches a curve at one and only one point.
In the video below we are going to look at tangents to curves and how we can use differentiation to find the gradient to a tangent and therefore the equation of a tangent. We will look at the example
Find the equation of the tangent to the curve y = x² at the point P(3, 9)
Notes from the video
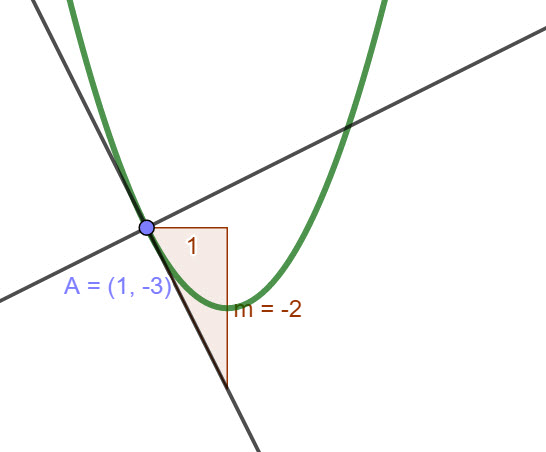
A normal line to a curve is the line that is perpendicular to the tangent to a curve at a particular point.
In the following video we are going to look at normals to curves, how we can use differentiation to find the gradient of a normal and therefore how to find the equation of a normal. In the example, we will also look at how to find the intersection of a normal with the curve
- Find the equation of the normal to the curve \(f(x)= \frac{1}{x}\)at the point P\((-2,-\frac{1}{2})\)
- Find the co-ordinates of the point where this normal meets the curve again.
Notes from the video
Print from here
Before you attempt to answer questions about equations of tangents and normals, you should be confident with finding the equation of a straight line and perpendicular lines. Here is a quiz that practices that knowledge
START QUIZ!
Here is a quiz about finding the equation of a tangent to a curve and the equation of a normal to a curve
START QUIZ!


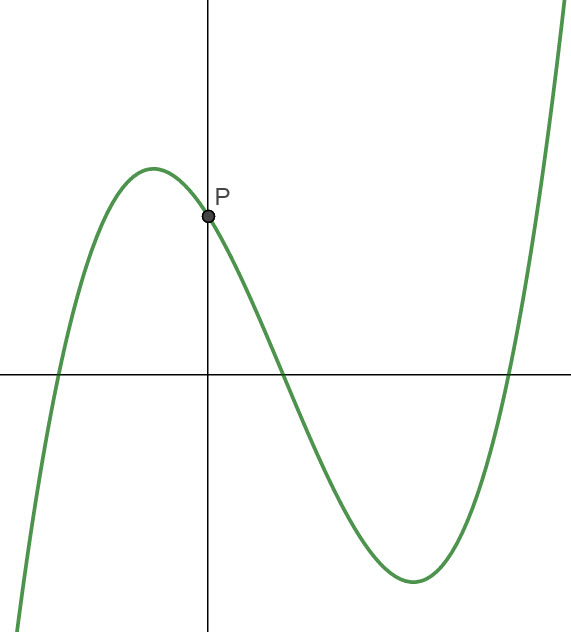
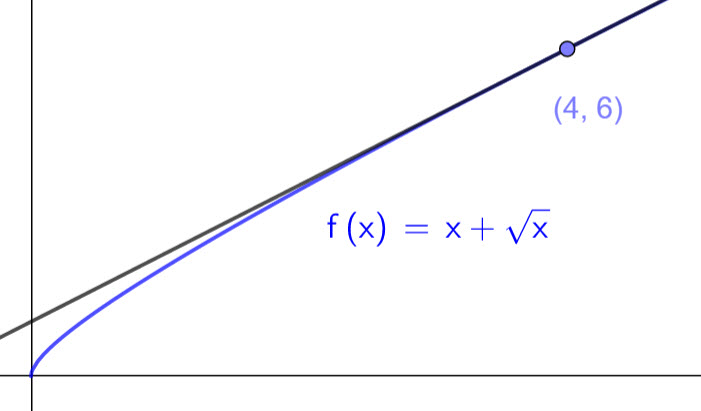
Let f(x) = (x - 1)(x - 4)(x + 2). The diagram below shows the graph of f and the point P where the graph crosses the x axis.
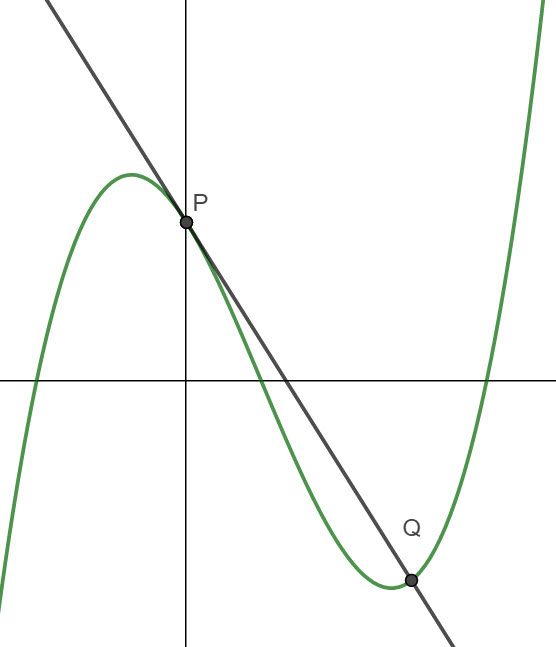
The line L is the tangent to the graph of f at the point P.
The line L intersects the graph of f at another point Q, as shown below
a) Find the coordinates of P
b) Show that \(f(x)=x^3-3x^2-6x+8\)
c) Find the equation of L in the form y = ax + b
d) Find the x coordinate of Q.
Hint
Full Solution
How much of Equation of Tangent and Normal have you understood?






 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn