\(\large \frac{y}{x}\) . We use a variable substitution \(\large (v=\frac{y}{x})\) and this turns our equation into a variables separable differential equation
On this page, you should learn about
recognising homogeneous differential equations in the form \(\large\frac{\mathrm{d}y}{\mathrm{d}x}=f(\frac{y}{x})\) solving homogeneous differential equations using the substitution \(y=vx\) The process for solving homogenous differential equations is always the same. However, it is quite a long one! The following video will help you understand what you need to know
In the following video we look at how we can solve homogenous differential equations. The process is quite long, there is a lot of algebraic manipulation, so the video is quite long. Grab a pen and work along with the video at the same time!
Use the substitution \(\large y=vx\) to solve the differential equation
\(\large 3xy^2\frac{\text{d}y}{\text{d}x}=x^3+y^3\)
The following quiz will give you some practice in recognising the type of differential equation to be solve: variables separable, integrating factor or homogeneous
Which type of differential equation is the following?
\(\large xy^2\frac{\text{d}y}{\text{d}x}=x+1\)
It is a variables separable differential equation.
We can rearrange it into the following
\(\large \int y^2{\text{d}y}=\int \frac{x+1}{x}{\text{d}x} \)
Which type of differential equation is the following?
\(\large x\frac{\text{d}y}{\text{d}x}=x+y\)
We can rearrange the equation as follows
\(\large \frac{\text{d}y}{\text{d}x}=\frac{x}{x}+\frac{y}{x}\)
\(\large \frac{\text{d}y}{\text{d}x}=1+\frac{y}{x}\)
Hence, the differential equation is homogeneous, that is, in the form \(\large \frac{\text{d}y}{\text{d}x}=f(\frac{y}{x}) \)
Which type of differential equation is the following?
\(\large x\frac{\text{d}y}{\text{d}x}+2y=x^2\)
We can rearrange the equation as follows
\(\large \frac{\text{d}y}{\text{d}x}+\frac{2}{x}y=x\)
The integrating factor is \(\large I=e^{\int \frac{2}{ x}dx }\)
Which type of differential equation is the following?
\(\large \frac{\text{d}y}{\text{d}x}+xy=e^x\)
This is in the correct form to use an integrating factor
The integrating factor is \(\large I=e^{\int x\ \text{d}x }\)
Which type of differential equation is the following?
\(\large \frac{\text{d}y}{\text{d}x}=e^{x-y}\)
It is a variables separable differential equation.
We can rearrange it into the following
\(\large \frac{\text{d}y}{\text{d}x}=\frac{e^x}{e^y}\)
\(\large \int e^y{\text{d}y}=\int e^x{\text{d}x}\)
Which type of differential equation is the following?
\(\large xy\frac{\text{d}y}{\text{d}x}-2x^2=y^2\)
We can rearrange the equation as follows
\(\large xy\frac{\text{d}y}{\text{d}x}=y^2+2x^2\)
\(\large \frac{\text{d}y}{\text{d}x}=\frac{y^2+2x^2}{xy}\)
\(\large \frac{\text{d}y}{\text{d}x}=\frac{\frac{y^2}{x^2}+\frac{2x^2}{x^2}}{\frac{xy}{x^2}}\)
\(\large \frac{\text{d}y}{\text{d}x}=\frac{(\frac{y}{x})^2+2 }{(\frac{y}{x})}\)
Hence, the differential equation is homogeneous, that is, in the form \(\large \frac{\text{d}y}{\text{d}x}=f(\frac{y}{x}) \)
Which type of differential equation is the following?
\(\large y \cos x \frac{\text{d}y}{\text{d}x}=e^y \sin x\)
It is a variables separable differential equation.
We can rearrange it into the following
\(\large \int ye^{-y}{\text{d}y}=\int \frac{\sin x}{\cos x}{\text{d}x}\)
Which type of differential equation is the following?
\(\large \sin x\frac{\text{d}y}{\text{d}x}+y \cos x=tanx\)
We can rearrange the equation
\(\large \frac{\text{d}y}{\text{d}x}+ \frac{\cos x}{\sin x}y=\frac{1}{\cos x}\)
This is in the correct form to use an integrating factor
The integrating factor is \(\large I=e^{\int \frac{\cos x}{\sin x}\ \text{d}x }\)
Which type of differential equation is the following?
\(\large \frac{\text{d}y}{\text{d}x}=\frac{x^2+y^2}{xy}\)
We can rearrange the equation as follows
\(\large \frac{\text{d}y}{\text{d}x}=\frac{\frac{x^2}{x^2}+\frac{y^2}{x^2}}{\frac{xy}{x^2}}\)
\(\large \frac{\text{d}y}{\text{d}x}=\frac{1+(\frac{y}{x})^2}{(\frac{y}{x})}\)
Hence, the differential equation is homogeneous, that is, in the form \(\large \frac{\text{d}y}{\text{d}x}=f(\frac{y}{x}) \)
Which type of differential equation is the following?
\(\large x\frac{\text{d}y}{\text{d}x}=y-\sqrt{x^2+y^2}\)
We can rearrange the equation as follows
\(\large \frac{\text{d}y}{\text{d}x}=\frac{y}{x}-\frac{\sqrt{x^2+y^2}}{x}\)
\(\large \frac{\text{d}y}{\text{d}x}=\frac{y}{x}-{\sqrt{1+\frac{y^2}{x^2}}}\)
\(\large \frac{\text{d}y}{\text{d}x}=\frac{y}{x}-{\sqrt{1+(\frac{y}{x})^2}}\)
Hence, the differential equation is homogeneous, that is, in the form \(\large \frac{\text{d}y}{\text{d}x}=f(\frac{y}{x}) \)
Consider the first order differential equation
\( \large xy\frac{\text{d}y}{\text{d}x}+4x^2+y^2=0 \quad,\quad y\geq0\)
a) Use the substitution y = vx \( \large \frac{\text{d}v}{\text{d}x}=-\frac{4+2v^2}{vx}\)
b) Show that the solution to the differential equation for which y(1) = 0 \(\large y=\frac{\sqrt{2-2x^4}}{x}\)
Divide both sides of the equations by x² to get in the recognisable form of a homogeneous differential equation
Consider the homogeneous differential equation \(\large \frac{\text{d}y}{\text{d}x}=\frac{x^2+y^2}{2xy}\)
a) Using the substitution y = vx \(\large \frac{\text{d}v}{\text{d}x}=\frac{1-v^2}{2vx}\)
b) Solve the differential equation and show that y² = x² - cx
Hint a) Divide the numerator and denominator by x² to get the differential equation in the required format to be able to substitute \(v=\frac{y}{x}\)
b) This is a variables separable differential equation
Full Solution
Consider the differential equation \(\large xy\frac{\text{d}y}{\text{d}x}=x^2\text{cosec}\frac{y}{x}+y^2\)
a) Show that this equation can be written in the form \(\large \frac{\text{d}y}{\text{d}x}=f(\frac{y}{x})\)
b) Using the substitution y = vx
Hint a) Divide the numerator and denominator by x² to get the differential equation in the required format to be able to substitute \(v=\frac{y}{x}\)
b) This is a variables separable differential equation
Full Solution MY PROGRESS
Self-assessment How much of Differential Equations - Homogeneous have you understood?
My notes
Which of the following best describes your feedback?
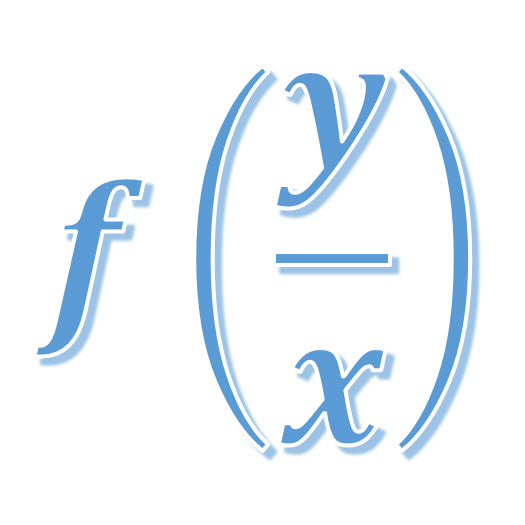 When a first order differential equation is not separable, nor linear (integrating factor), it may still be possible to solve it analytically using a substitution. This will work when the equation is homogeneous. A homogenous differential equation is a differential equation that can be written as a function of \(\large \frac{y}{x}\). We use a variable substitution \(\large (v=\frac{y}{x})\) and this turns our equation into a variables separable differential equation
When a first order differential equation is not separable, nor linear (integrating factor), it may still be possible to solve it analytically using a substitution. This will work when the equation is homogeneous. A homogenous differential equation is a differential equation that can be written as a function of \(\large \frac{y}{x}\). We use a variable substitution \(\large (v=\frac{y}{x})\) and this turns our equation into a variables separable differential equation



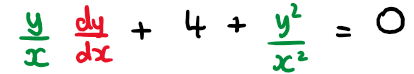
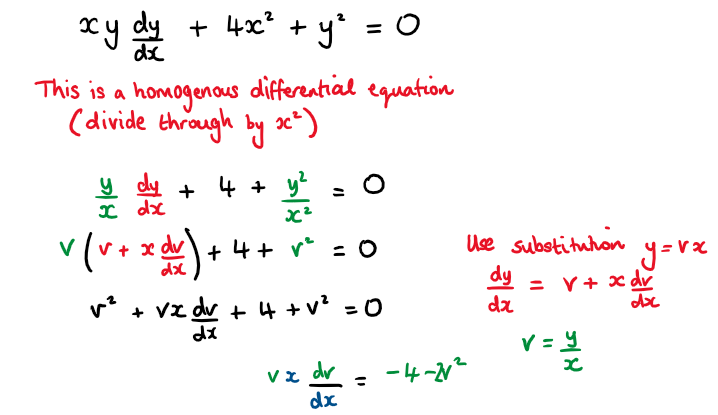
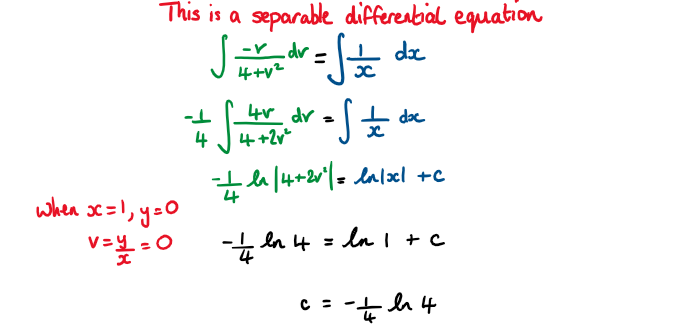
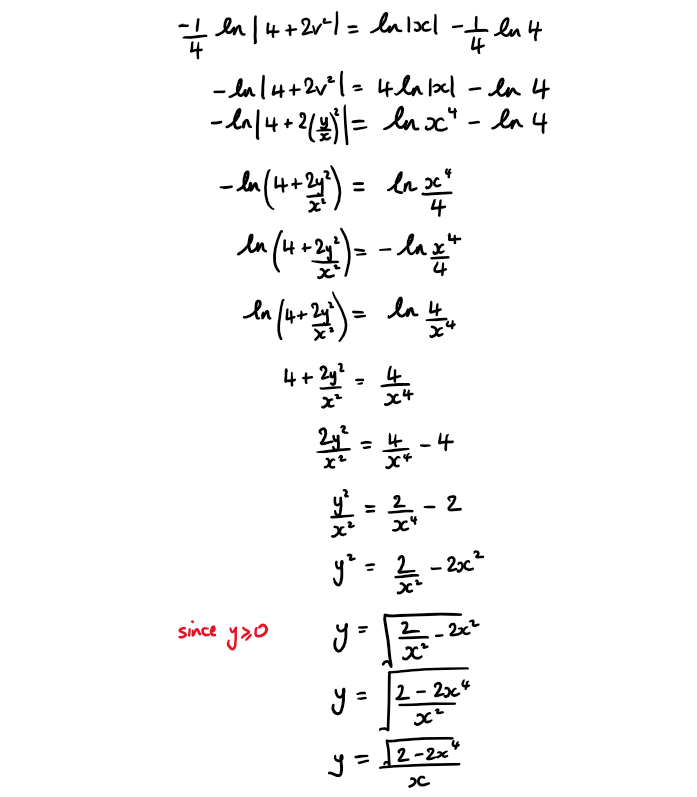

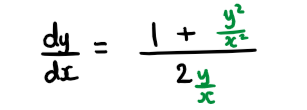
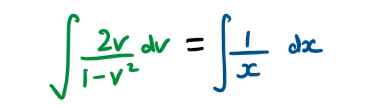


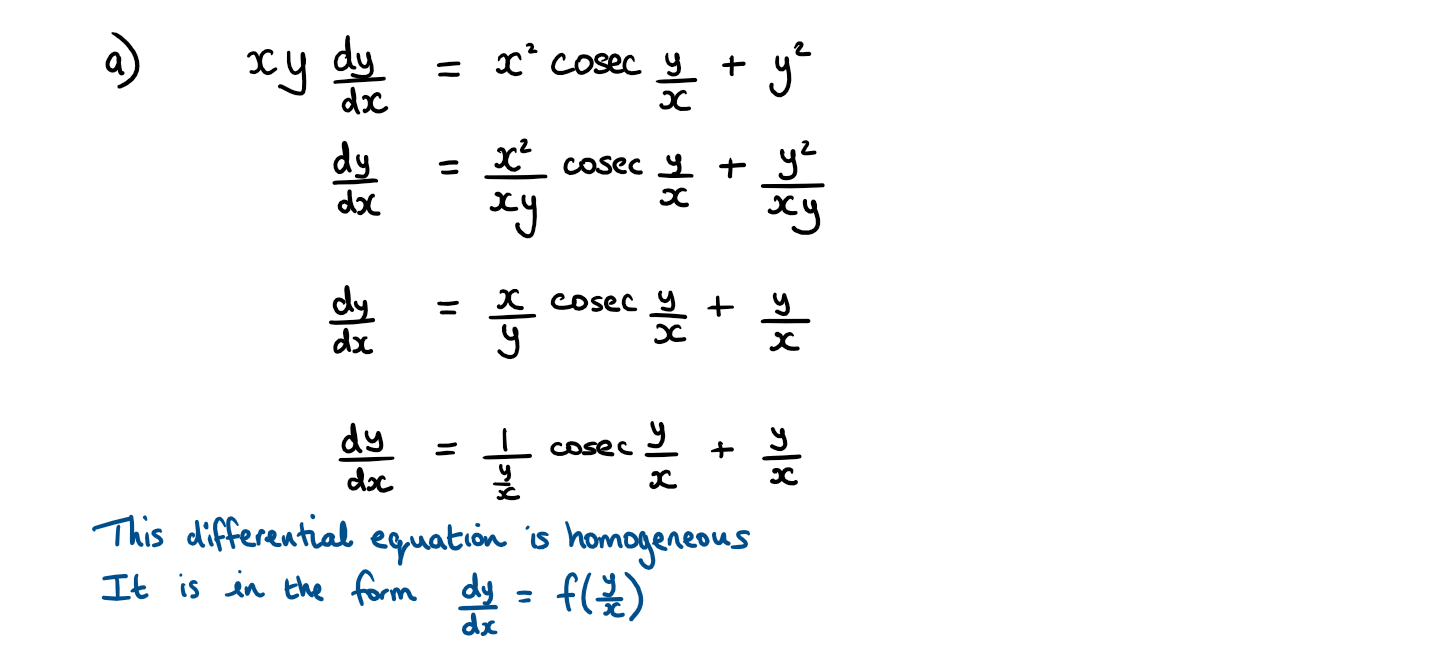
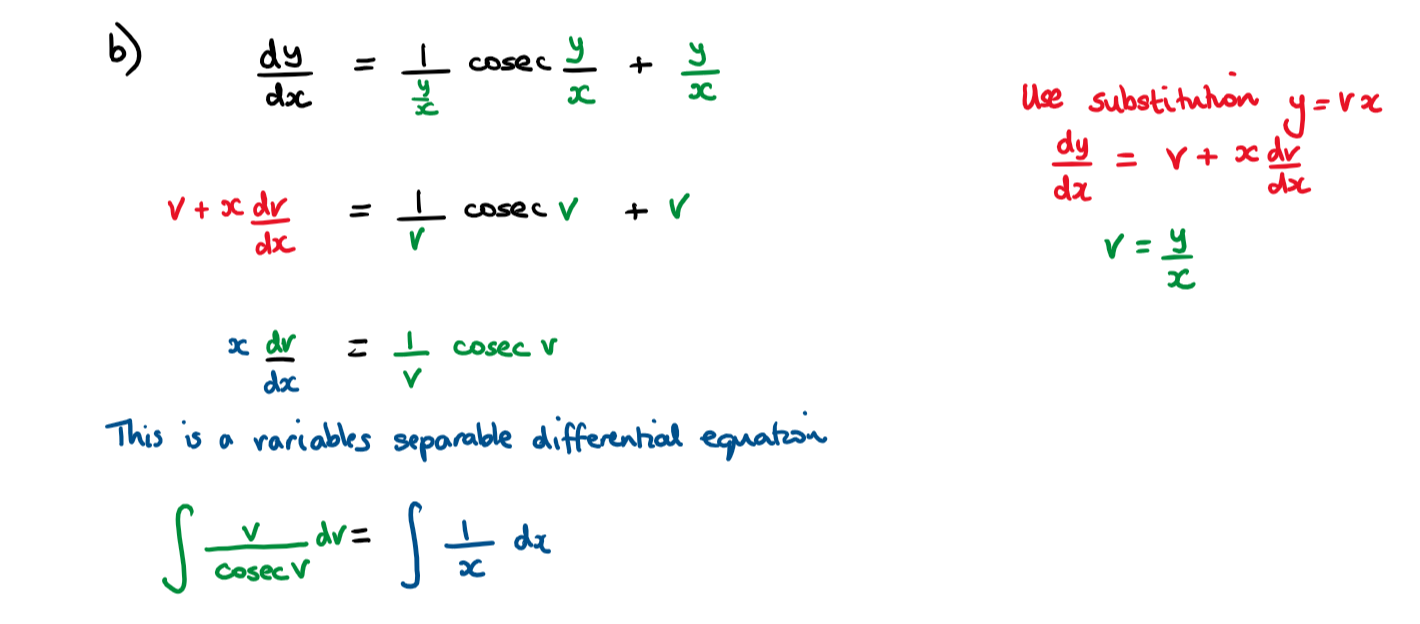
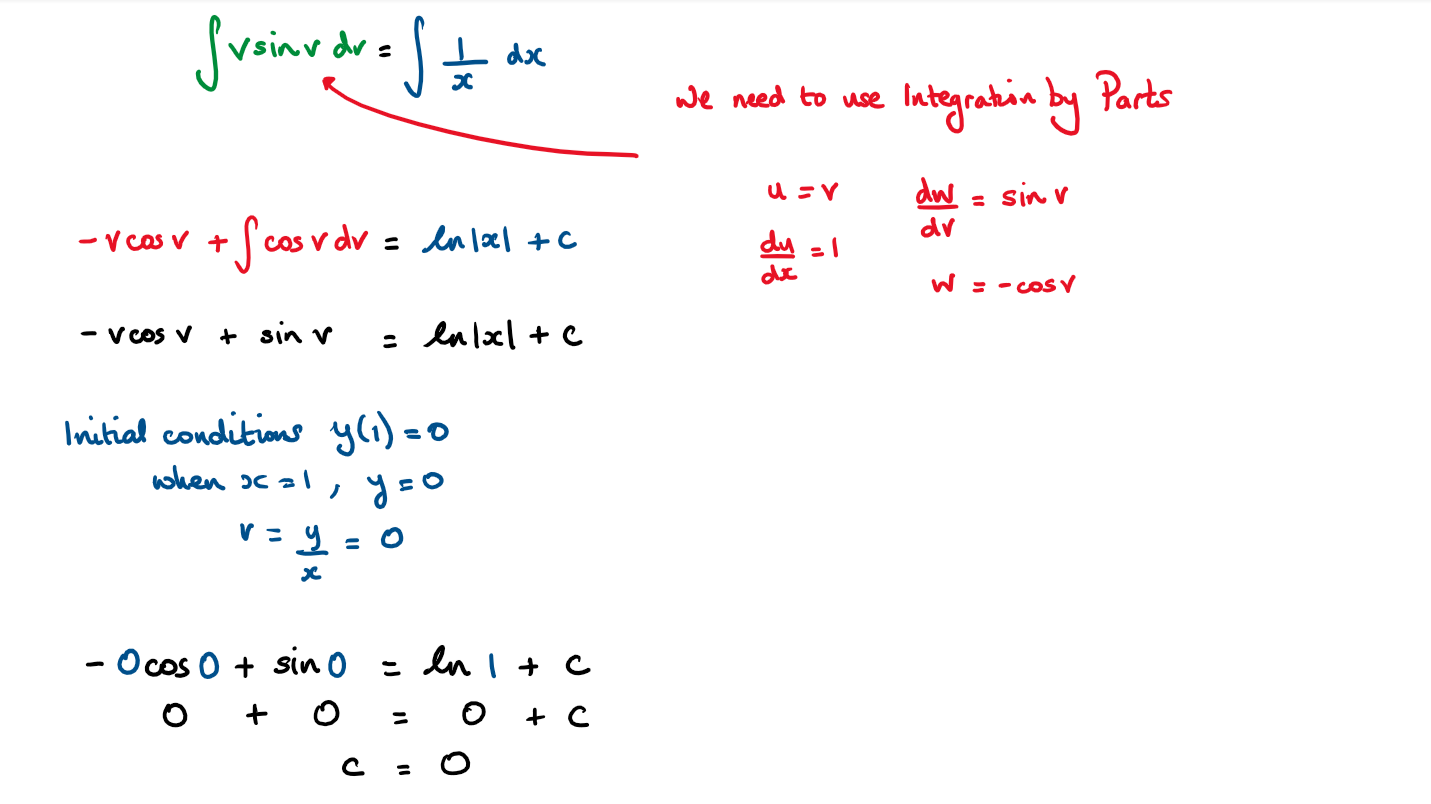
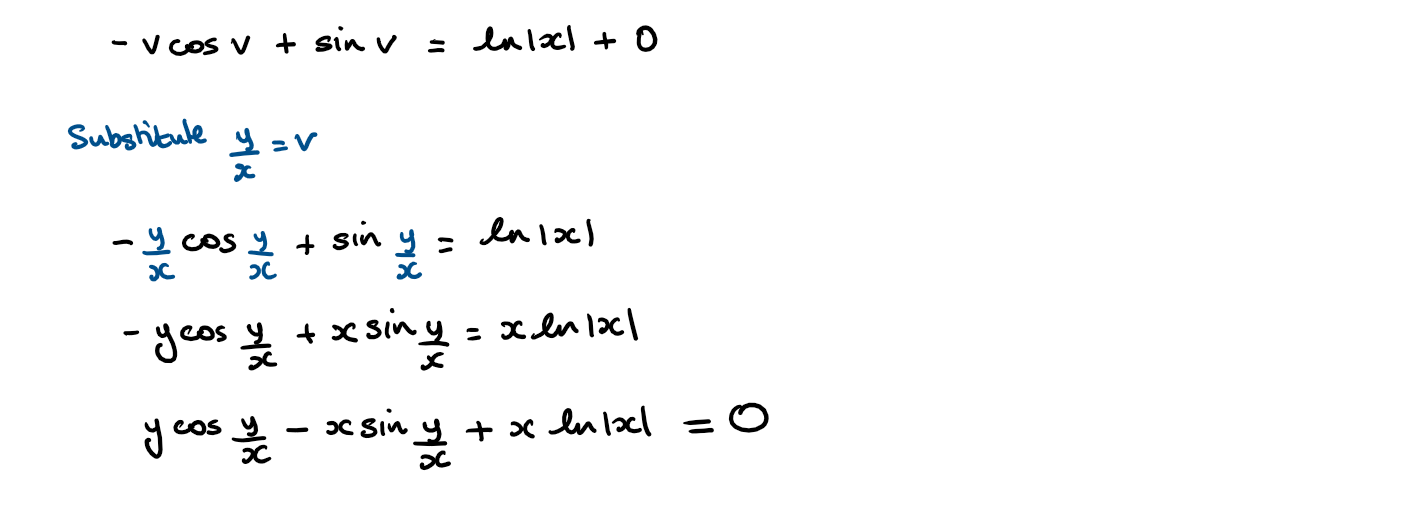
 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn