 Optimisation questions involve finding the best solution to a problem. Usually, that is the maximum or minimum value of a function. Questions on this topic require you to take information from a practical problem and write this as a function, then use differentiation to find the maximum or minimum value of this function by solving where the gradient is equal to zero. Often questions on this topic seem to have two variables, but you need to take a piece of information that fixes one of the variables and substitute this to create a function with one variable (although HL students might have to use Implicit Differentiation!)
Optimisation questions involve finding the best solution to a problem. Usually, that is the maximum or minimum value of a function. Questions on this topic require you to take information from a practical problem and write this as a function, then use differentiation to find the maximum or minimum value of this function by solving where the gradient is equal to zero. Often questions on this topic seem to have two variables, but you need to take a piece of information that fixes one of the variables and substitute this to create a function with one variable (although HL students might have to use Implicit Differentiation!)
On this page, you should learn about
- solving optimisation problems using differentiation
The following videos will help you understand all the concepts from this page
Optimum Can
In the following video we look at an example of using differentiation to find the best possible can for a drinks manufacturer.
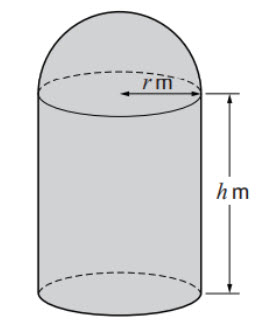
A drinks manufacturer wants a design for a new can for their mini drinks collection, volume=170ml.Your job is to find the can that will contain a volume of 170ml = 170cm3 ≈54πcm3 and that will minimize the amount of aluminium used.
It might help you to visualize the can by playing with the following applet
Notes from the video
The following is an example of an optimisation problem
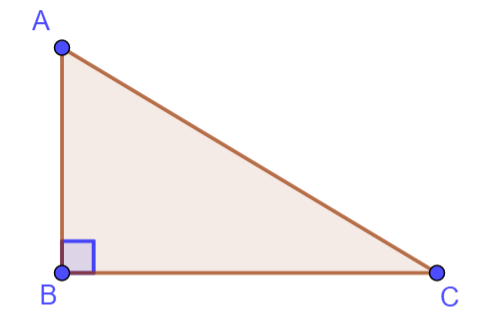
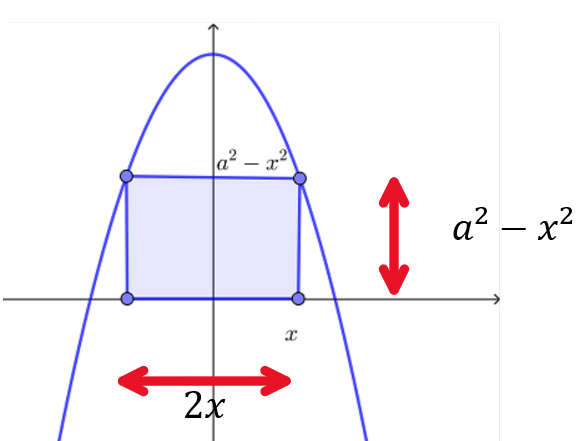
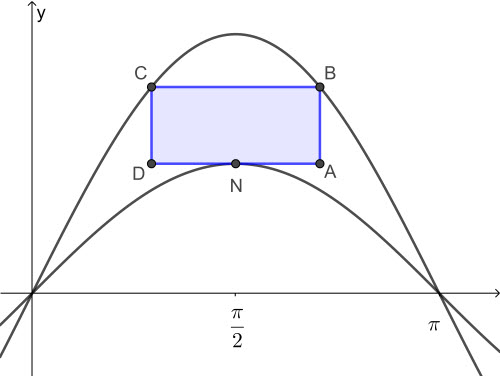
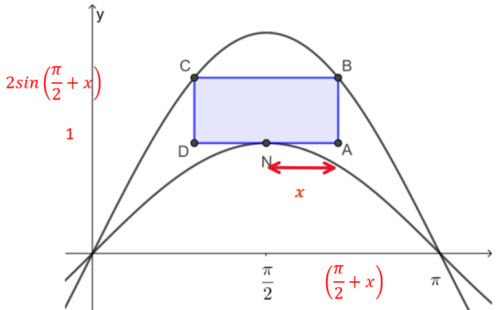
A rectangle ABCD is drawn so that its lower vertices are on the x-axis and its upper vertices are on the curve \(f(x)=\sqrt{6-3x^2}\) as shown in the following diagram
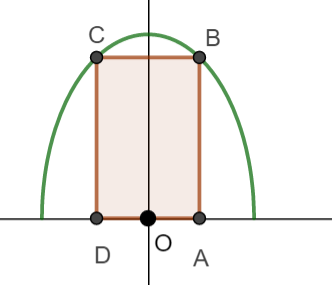
Let OA = x
The area of this rectangle is denoted by A.
(a) Write down an expression for A in terms of x.
(b) Find the maximum value of A.
You may find the following applet useful to get an understanding of the problem.
Notes from the video
Here is a quiz that practises setting up the problem before you use Calculus to solve. You are strongly recommended to have something to write with whilst doing these questions. You may want to draw sketches of shapes and graphs to help you think through the problems. You are not required to do any Calculus in this quiz!
START QUIZ!
How much of Optimisation have you understood?



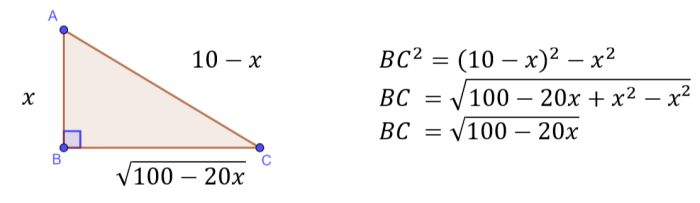






 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn