 This page is about finding related rates of change, otherwise know as connected rates of change. In questions on this topic, you will be given a rate of change of some quantity and be required to find the rate of change of another, that is related to the first by some relationship. This is an application of the Chain Rule and a knowlegde of implicit differentiation is helpful.
This page is about finding related rates of change, otherwise know as connected rates of change. In questions on this topic, you will be given a rate of change of some quantity and be required to find the rate of change of another, that is related to the first by some relationship. This is an application of the Chain Rule and a knowlegde of implicit differentiation is helpful.
On this page, you should learn how to
- Connect rates of change using the Chain Rule
- Solve problems with Related rates of Change using Implicit Differentiation
A right circular cone is being filled with water. Initially the cone is empty, then water is added at \(\large 6\pi\) cm3s-1. At the time when the radius is 3cm, the volume of the solid is \(\large 15\pi\) cm3, the radius is changing at a rate of 0.5 cms-1.
Find the rate of change of the depth of water at this time.
Try this quiz to practise the skills from this page
START QUIZ!
Related Rates of Change 1/1
A = 4x²
Find \(\large \frac{dA}{dt}\) when x = 4 and \(\large \frac{dx}{dt}=1.5\)
\(\large \frac{dA}{dt}\)=
\(\large A = 4x²\)
Use Implicit differentiation to differentiate with respect to t
\(\large \frac{dA}{dt}=8x\cdot\frac{dx}{dt}\)
\(\large \frac{dA}{dt}=8\times4\times1.5=48\)
E = 5v²
Find \(\large \frac{dE}{dt}\) when v = 3 and \(\large \frac{dv}{dt}=0.5\)
\(\large \frac{dE}{dt}\)=
\(\large E=5v^2\)
Use Implicit differentiation to differentiate with respect to t
\(\large \frac{dE}{dt}=10v\cdot\frac{dv}{dt}\)
\(\large \frac{dE}{dt}=10\times3\times0.5=15\)
\(\large V=\frac{4}{3}\pi r^3\)
Find \(\large \frac{dV}{dt}\) when r = 5 and \(\large \frac{dr}{dt}=\frac{3}{\pi}\)
\(\large \frac{dV}{dt}\)=
\(\large V=\frac{4}{3}\pi r^3\)
Use Implicit differentiation to differentiate with respect to t
\(\large \frac{dV}{dt}=4\pi r^2\cdot\frac{dr}{dt}\)
\(\large \frac{dV}{dt}=4\pi \times 5^2\times\frac{3}{\pi}=300\)
\(\large A = 4\pi r²\)
When r = 4 and \(\large \frac{dr}{dt}=0.25\), then \(\large \frac{dA}{dt}=k\pi\)
Find the value of k
k =
\(\large A = 4\pi r²\)
Use Implicit differentiation to differentiate with respect to t
\(\large \frac{dA}{dt}=8\pi r\cdot\frac{dr}{dt}\)
\(\large \frac{dA}{dt}=8\pi \times4\times0.25=8\pi\)
\(\large x=2\sin \theta\)
Find \(\large \frac{dx}{dt}\) when \(\large \theta=\frac{\pi}{6}\) and \(\large \frac{d\theta}{dt}=\sqrt{3}\)
\(\large \frac{dx}{dt}\)=
\(\large x=2\sin \theta\)
Use Implicit differentiation to differentiate with respect to t
\(\large \frac{dx}{dt}=2\cos \theta\cdot\frac{d\theta}{dt}\)
\(\large \frac{dx}{dt}=2 \cos (\frac{\pi}{6})\times \sqrt{3}\)
\(\large \frac{dx}{dt}=2 \times \frac{\sqrt{3}}{2}\times \sqrt{3}\)
\(\large \frac{dx}{dt}=3\)
The sides of a cube are increasing at 0.5 cms-1
When the sides of the cube are 5cm, what is the rate at which the surface area is increasing?
Answer = cm²s-1
The surface area, \(\large A=6x^2\)
Use Implicit differentiation to differentiate with respect to t
\(\large \frac{dA}{dt}=12x\cdot\frac{dx}{dt}\\ \large \frac{dA}{dt}=12\times5\times 0.5=30\)
The radius of a circle is increasing at a rate of 2cm per min. When the radius is 10cm, the rate the area is increasing is \(\large k\pi\).
Find the value of k
k =
The area, \(\large A=\pi r^2\)
Use Implicit differentiation to differentiate with respect to t
\(\large \frac{dA}{dt}=2\pi r\cdot\frac{dr}{dt}\\ \large \frac{dA}{dt}=2\pi \times10\times 2=40\pi\)
The edges of a cube are increasing at 2 cm per minute.
When the edges of the cube are 6 cm, what is the rate at which the volume is increasing?
Answer =
The volume of the cube, \(\large V=x^3\)
Use Implicit differentiation to differentiate with respect to t
\(\large \frac{dV}{dt}=3x^2\cdot\frac{dx}{dt}\\ \large \frac{dV}{dt}=3\times6^2\times 2=216\)
A hemispherical bowl with radius 10 cm is being filled with water.
The volume of water can be found using the formula \(\large V=10\pi h^2-\frac{1}{3}\pi h^3\)
The rate at which the volume is increasing is \(\large 15\pi\) cm3 s-1
Find the rate at which the height of water is increasing when h = 5cm
Answer =
\(\large V=10\pi h^2-\frac{1}{3}\pi h^3\)
Use Implicit differentiation to differentiate with respect to t
\(\large \frac{dV}{dt}=20 \pi h\cdot\frac{dh}{dt}- \pi h^2\cdot\frac{dh}{dt}\\ \large 15\pi=20 \pi \times 5\times\frac{dh}{dt}- \pi \times 5^2\cdot\frac{dh}{dt}\\ \large 15\pi=100 \pi \frac{dh}{dt}- 25\pi \frac{dh}{dt}\\ \large 15\pi=75 \pi \frac{dh}{dt}\\ \large \frac{dh}{dt}=0.2\)
The radius of a cone is 6cm. The radius is increasing at 0.5 cms-1.
The height of the same cone is 5cm. The height is increasing at a rate of 1cms-1.
The rate at which the volume of the cone is increasing is \(\large k\pi\) cm3s-1.
Find k
The formula for the volume of a cone, \(\large V=\frac{1}{3}\pi r^2h\)
k =
\(\large V=\frac{1}{3}\pi r^2h\)
Use Implicit differentiation to differentiate with respect to t
r and h are both variables, and so we should consider that \(\large r^2\cdot h\) is a product and we need to use the Product Rule:
\(\large \frac{dV}{dt}=\frac{1}{3}\pi(r^2\cdot h) \\ \large \frac{dV}{dt}=\frac{1}{3}\pi (2r\frac{dr}{dt}\cdot h+r^2\cdot \frac{dh}{dt})\\ \large \frac{dV}{dt}=\frac{1}{3}\pi (2\times6\times 0.5\times 5+6^2\times1)\\ \large \frac{dV}{dt}=\frac{1}{3}\pi(66)\\ \large \frac{dV}{dt}=22\pi\)
text

The radius of a sphere is increasing at 2.5 cms-1
Find the rate at which the volume of the sphere is increasing when the radius is 8 cm.
Give your answer in terms of \(\large \pi\)
Hint
The rate at which the volume of the sphere is increasing is \(\large \frac{dV}{dt}\)
To find it, use the chain rule
\(\large \frac{dV}{dt}=\)\(\large \frac{dV}{dr}\)\(\large \times\)\(\large \frac{dr}{dt}\)
Full Solution
The volume of a sphere, \(\large V = \frac{4}{3}\pi r^3\)
Differentiate with respect to r , \(\large \frac{dV}{dr}=4\pi r^2\)
When r = 8 cm , \(\large \frac{dV}{dr}=4\pi \times 8^2=256 \pi\)
The radius of a sphere is increasing at 2.5 cms-1, \(\large \frac{dr}{dt}=2.5\)
Using the chain rule
\(\large \frac{dV}{dt}=\)\(\large \frac{dV}{dr}\)\(\large \times\)\(\large \frac{dr}{dt}\)
\(\large \frac{dV}{dt}=\)\(\large 256 \pi\)\(\large \times\)\(\large 2.5\)
\(\large \frac{dV}{dt}=640 \pi\)

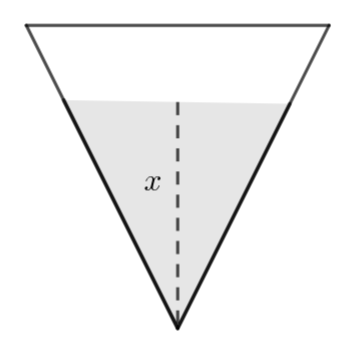 The diagram shows a container in the form of a right circular cone. The height of the cone is equal to its diameter. Initially the cone is empty, then water is added at a rate of \(\large 18\pi\) cm3 per minute. the depth of water in the container at the time is given by h cm.
The diagram shows a container in the form of a right circular cone. The height of the cone is equal to its diameter. Initially the cone is empty, then water is added at a rate of \(\large 18\pi\) cm3 per minute. the depth of water in the container at the time is given by h cm.
a) Show that the volume, V cm3 , of water in the container when the depth is x cm is given by
\(\large V=\frac{1}{12} \pi x^3\)
b) Find the rate at which the depth of the water is increasing at the instant when the depth is 12 cm
Hint
a) height = diameter
Therefore, \(\large r=\frac{h}{2}\)
In this case, the height of water = x
b) The rate at which the depth of the water is increasing is \(\large \frac{dx}{dt}\)
To find it, use the chain rule
\(\large \frac{dV}{dt}\)=\(\large \frac{dV}{dx}\)\(\large \times\)\(\large \frac{dx}{dt}\)
Full Solution
a) The volume of a cone, \(\large V = \frac{1}{3}\pi r^2h\)
In this case the height = diameter
Therefore, \(\large r=\frac{h}{2}\)
The volume of a cone, \(\large V = \frac{1}{3}\pi (\frac{h}{2})^2h\\ \large V = \frac{1}{3}\pi (\frac{h^2}{4})h\\ \large V = \pi \frac{h^3}{12}\)
When the depth (height) of water= x, then
\(\large V=\frac{1}{12} \pi x^3\)
b) \(\large V=\frac{1}{12} \pi x^3\)
Differentiate with respect to x , \(\large \frac{dV}{dx}=\frac{1}{4}\pi r^2\)
When x = 12 cm , \(\large \frac{dV}{dx}=\frac{1}{4}\pi \times12^2=36\pi\)
Water is added at a rate of \(\large 18\pi\) cm3 per minute, \(\large \frac{dV}{dt}=18 \pi\)
Using the chain rule
\(\large \frac{dV}{dt}\)=\(\large \frac{dV}{dx}\)\(\large \times\)\(\large \frac{dx}{dt}\)
\(\large 18 \pi\) =\(\large36\pi\)\(\large \times\)\(\large \frac{dx}{dt}\)
\(\large \frac{dx}{dt}=\frac{18\pi}{36\pi}\)
\(\large \frac{dx}{dt}=0.5\) cm per minute

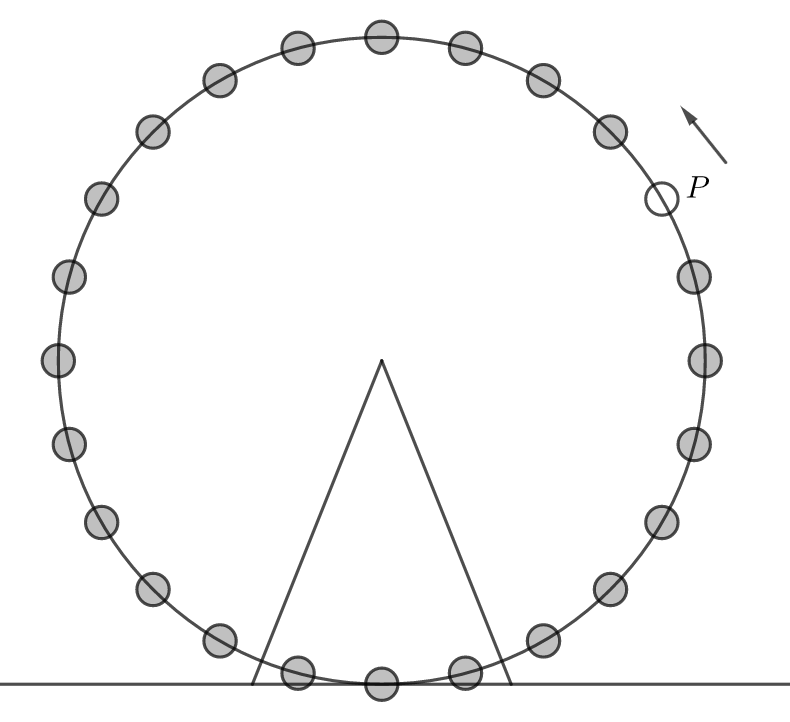
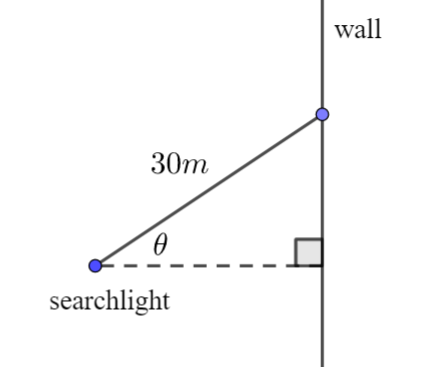
A searchlight rotates at 2 revolutions per minute. The beam hits a wall 30m away and produces a spot of light that moves horizontally along the wall. How fast is the spot moving along the wall when the angle, \(\large \theta\) between the beam and the line through the spotlight perpendicular to the wall is 45°?
Hint
If we let x be the distance along the wall, then the speed of the spotlight is\(\large \frac{dx}{dt}\)
To find it, use the chain rule
\(\large \frac{dx}{dt}\)=\(\large \frac{dx}{d\theta}\)\(\large \times\)\(\large \frac{d\theta}{dt}\)
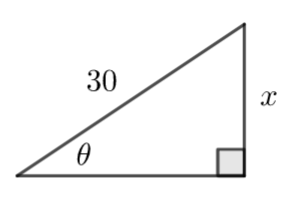
To find \(\large \frac{dx}{d\theta}\) use right-angled triangle trigonometry to find x in terms of \(\large \theta\)
Full Solution
The searchlight is rotating at 2 revolutions per minute
1 revolution is \(\large 2\pi \) radians
Therefore, \(\large \frac{d\theta}{dt}=4\pi\) radians per minute
Let the distance fom from the perpendicular be x

\(\large \sin \theta=\frac{x}{30}\)
\(\large x=30 \sin\theta\)
Differentiate with respect to \(\large \theta\)
\(\large \frac{dx}{d\theta}=30 \cos \theta\)
When \(\theta\)=45°, \(\large \frac{dx}{d\theta}=30 \cos45°=15\sqrt{2}\)
Use the chain rule
\(\large \frac{dx}{dt}\)=\(\large \frac{dx}{d\theta}\)\(\large \times\)\(\large \frac{d\theta}{dt}\)
\(\large \frac{dx}{dt}\)=\(\large 15\sqrt{2}\)\(\large \times\)\(\large 4\pi\)
\(\large \frac{dx}{dt}=60\sqrt{2}\pi\approx267\)m per minute

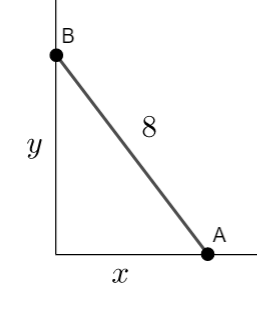
A ladder AB of length 8m has one endA on horizontal ground and the other end B resting against a vertical wall.
The end A slips away from the wall at a constant speed of 0.5 ms-1 and the end B slips down the wall.
Determine the speed of the end B is slipping down the wall when the top of the ladder is 5 m above the ground.
Hint
If we let x be the distance along the ground, then the speed end A slips away from the wall is \(\large \frac{dx}{dt}\)
If w let y be the distance up the wall, then the speed end B slips down the wall is \(\large \frac{dy}{dt}\)
Use Pythagoras' Theorem
Full Solution
The speed end A slips away from the wall is \(\large \frac{dx}{dt}\)
\(\large \frac{dx}{dt}=0.5\) ms-1
The speed end B slips down the wall is \(\large \frac{dy}{dt}\)
Using Pythagoras' Theorem
\(\large x^2+y^2=8^2\)
\(\large x^2+y^2=64\)
Differentiate with respect to t (implicit differentiation)
\(\large 2x \frac{dx}{dt}+2y\frac{dy}{dt}=0\)
When y =5 ,
\(\large x^2+5^2=64\\ \large x^2=39\\ \large x=\sqrt {39}\)
Substitute these values in the differential equation
\(\large 2x \frac{dx}{dt}+2y\frac{dy}{dt}=0\)
\(\large 2\sqrt{39}\times 0.5+2\times 5\frac{dy}{dt}=0\\ \large 10\frac{dy}{dt}=-\sqrt{39}\\ \large \frac{dy}{dt}=-\frac{\sqrt{39}}{10}\\ \large \frac{dy}{dt}=-0.624\)
Notice that the value is negative. This represents the velocity and shows that it is slipping down.
The speed is 0.624 ms-1

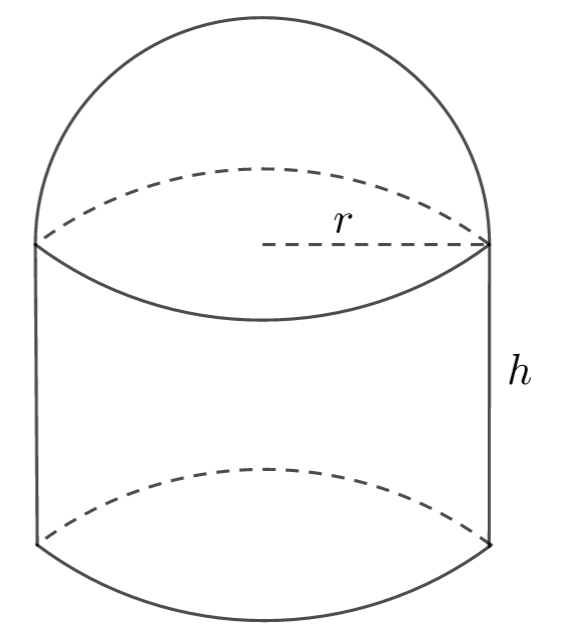
A solid is made up of a cylinder and a hemisphere as shown in the diagram.
a) Write down a formula for the volume of the solid.
b) At the time when the radius is 6cm, the volume of the solid is \(\large 684\pi\) cm3 , the radius is changing at a rate of 1.5 cm/minute and the volume is changing at a rate of \(\large 1800\pi\) cm3 /min. Find the rate of change of the height at this time.
Hint
We can find the volume of the solid to be \(\large V=\frac{2}{3}\pi r^3+\pi r^2h\)
We know \(\large \frac{dr}{dt}\) and \(\large \frac{dV}{dt}\). We are required to find \(\large \frac{dh}{dt}\).
Use implicit differentiation and differentiate the formula for V with respect to t
Full Solution
a) The volume of a hemisphere is \(\large \frac{2}{3}\pi r^3\)
The volume of a cylinder is \(\large \pi r^2h\)
The volume of the solid, \(\large V=\frac{2}{3}\pi r^3+\pi r^2h\)
b) We can find the value of h when r = 6 and V = \(\large 684\pi\)
\(\large 684\pi=\frac{2}{3}\pi \times 6^3+\pi \times 6^2\times h\\ \large 684\pi=144\pi+36\pi h\\ \large 540\pi=36\pi h\\ \large h = 15\)
The radius is changing at a rate of 1.5 cm/minute, \(\large \frac{dr}{dt}=1.5\)
The volume is changing at a rate of \(\large 1800\pi\) cm3 /min, \(\large \frac{dV}{dt}=1800\pi\)
We are required to find \(\large \frac{dh}{dt}\).
Use implicit differentiation and differentiate the formula for V with respect to t
\(\large V=\frac{2}{3}\pi r^3+\pi r^2h\)
Notice that the second part of the expression 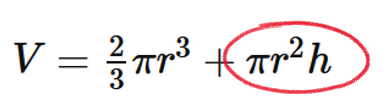 is a product (both r and h are variables). Therefore we need to use the Product Rule for differentiation
is a product (both r and h are variables). Therefore we need to use the Product Rule for differentiation
\(\large \frac{dV}{dt}=2\pi r^2\frac{dr}{dt}+\pi r^2\frac{dh}{dt}+2\pi r^2\frac{dr}{dt}\cdot h\)
\(\large 1800\pi=2\pi \times 6^2\times 1.5+\pi \times 6^2\frac{dh}{dt}+2\pi \times 6^2\times 1.5\times 15\\ \large 1800\pi=108\pi+36\pi \cdot \frac{dh}{dt}+1620\pi\\ \large 72\pi=36\pi \cdot \frac{dh}{dt}\\ \large \frac{dh}{dt}=2\)
\(\large \frac{dh}{dt}=2\) cm/min
How much of Related Rates of Change have you understood?
Feedback
Which of the following best describes your feedback?




 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn