This page is ideal for practising all the skills of integration. You may wish to use this page in preparation for a test on this topic or for the final examinations. The quizzes on this page have been carefully created to take you through all the skills that you need. If you want a more in depth look, then you should go to the individual pages on these topics.
On this page, you can practise questions on
- standard integrals
- Integration by recognition
- integration by substitution
- definite integrals
- areas between graphs
- kinematics
Here's a quiz that practises the Standard Integrals: \((ax+b)^n , e^{ax}, sin(ax+b), cos(ax+b) \)
START QUIZ!
Mixed SL Integration 1 1/1
Work out \(\int { 2sin(3x+1)dx } \)
Use the standard result \(\int { sin(ax+b)dx } =-\frac { cos(ax+b) }{ a } +C\)
Work out \(\int { \frac { cos(0.5x-2) }{ 2 } dx } \)
Use the standard result \(\int { cos(ax+b)dx } =\frac { sin(ax+b) }{ a } +C\)
Work out \(\int { { e }^{ 2x-1} }dx\)
Use the standard result \(\int { { e }^{ ax+b }dx=\frac { { e }^{ ax+b } }{ a } } +C\)
Work out \(\int { \frac { 1 }{ 2x+3 }} dx\)
Use the standard result \(\int { \frac { 1 }{ ax+b } dx=\frac { 1 }{ a } } ln\left| ax+b \right| +C\)
Work out \(\int { (3x-1)^{ 4 } } dx\)
Use the standard result \(\int { (ax+b)^{ n }dx=\frac { (ax+b)^{ n+1 } }{ a(n+1) } +C } \)
Work out \(\int { \frac { \sqrt { 3x+1 } }{ 2 } dx } \)
Use the standard result \(\int { (ax+b)^{ n }dx=\frac { (ax+b)^{ n+1 } }{ a(n+1) } +C } \)
\(\int { \frac { \sqrt { 3x+1 } }{ 2 } dx } =\frac{1}{2}\int { { (3x+1) }^{ \frac{1}{2} } dx}\)
\(=\frac { 1 }{ 2 } \frac { { (3x+1) }^{ \frac { 3 }{ 2 } } }{ 3\left( \frac { 3 }{ 2 } \right) } +C\)
\(=\frac { { (3x+1) }^{ \frac { 3 }{ 2 } } }{ 9 } +C\)
Work out \(\int { \frac { 3 }{ { (2+5x) }^{ 2 } } dx } \)
Use the standard result \(\int { (ax+b)^{ n }dx=\frac { (ax+b)^{ n+1 } }{ a(n+1) } +C } \)
\(\int { \frac { 3 }{ { (2+5x) }^{ 2 } } dx } =3\int { (2+5x)^{ -2 }dx } \)
\(=3\frac { { (2+5x) }^{ -1 } }{ (-1)5 } +C\)
\(-\frac { 3 }{ 5(2+5x) } +C\)
Work out \(\int { \frac { 4 }{ \sqrt { 2x-1 } } dx } \)
Use the standard result \(\int { (ax+b)^{ n }dx=\frac { (ax+b)^{ n+1 } }{ a(n+1) } +C } \)
\(\int { \frac { 4 }{ \sqrt { 2x-1 } } dx } =4\int { (2x-1)^{ -\frac { 1 }{ 2 } }dx } \)
\(=4\frac { { (2x-1) }^{ \frac { 1 }{ 2 } } }{ (2)\left( \frac { 1 }{ 2 } \right) } +C\)
\(=4\sqrt { 2x-1 } +C\)
Work out \(\int { \frac { 4 }{ { e }^{ 3x } } dx }\)
Use the standard result \(\int { { e }^{ ax+b }dx=\frac { { e }^{ ax+b } }{ a } } +C\)
\(\int { \frac { 4 }{ { e }^{ 3x } } dx } =4\int { { e }^{ -3x }dx}\)
\(=4\frac { { e }^{ -3x }}{ { -3 } } +C\)
\(=-\frac { 4 }{ 3{ e }^{ 3x } } +C\)
Work out \(\int { \sqrt { { e }^{ 4x } } dx } \)
Use the standard result \(\int { { e }^{ ax+b }dx=\frac { { e }^{ ax+b } }{ a } } +C\)
\(\int { \sqrt { { e }^{ 4x } } dx } =\int { { \left( { e }^{ 4x } \right) }^{ \frac { 1 }{ 2 } }dx } \)
\(=\int { { { e }^{ 2x } }dx } \)
\(=\frac { { e }^{ 2x } }{ 2 } +C\)
Here is a quiz that practises Integration by Recognition in the form \(\large\int{f'(x)e^{f(x)}{dx}}\)
START QUIZ!
Integration by recognition 1 1/1
Work out \(\large\int{2xe^{x^2}{dx}}\)
This is an integration by recognition question in the form \(\large\int{f'(x)e^{f(x)}{dx}}=e^{f(x)}+C\)
We can also use integration by substitution with the substitution \(u=x^2\)
Work out \(\large\int{\cos xe^{\sin x}{dx}}\)
This is an integration by recognition question in the form \(\large\int{f'(x)e^{f(x)}{dx}}=e^{f(x)}+C\)
We can also use integration by substitution with the substitution \(u=\sin x\)
Work out \(\large\int{\sin xe^{\cos x}{dx}}\)
This is an integration by recognition question in the form \(\large\int{f'(x)e^{f(x)}{dx}}=e^{f(x)}+C\)
We can also use integration by substitution with the substitution \(u=\cos x\)
Work out \(\large\int{x^2e^{x^3}{dx}}\)
This is an integration by recognition question in the form \(\large\int{f'(x)e^{f(x)}{dx}}=e^{f(x)}+C\)
We can also use integration by substitution with the substitution \(u=x^3\)
Work out \(\large\int{x^3e^{x^4}{dx}}\)
This is an integration by recognition question in the form \(\large\int{f'(x)e^{f(x)}{dx}}=e^{f(x)}+C\)
We can also use integration by substitution with the substitution \(u=x^4\)
Work out \(\large\int{(x+1)e^{x^2+2x}{dx}}\)
This is an integration by recognition question in the form \(\large\int{f'(x)e^{f(x)}{dx}}=e^{f(x)}+C\)
We can also use integration by substitution with the substitution \(u=x^2+2x\)
Work out \(\large\int{\frac{e^{\sqrt{x}}}{\sqrt{x}}{dx}}\)
This is an integration by recognition question in the form \(\large\int{f'(x)e^{f(x)}{dx}}=e^{f(x)}+C\)
We can also use integration by substitution with the substitution \(u=x^{0.5}\)
Work out \(\large\int{\cos 2x\ e^{\sin 2x}{dx}}\)
This is an integration by recognition question in the form \(\large\int{f'(x)e^{f(x)}{dx}}=e^{f(x)}+C\)
We can also use integration by substitution with the substitution \(u=\sin 2x\)
Work out \(\large\int{(1+\ln x)e^{x \ln x}{dx}}\)
This is an integration by recognition question in the form \(\large\int{f'(x)e^{f(x)}{dx}}=e^{f(x)}+C\)
We can also use integration by substitution with the substitution \(u=x\ln x\)
We use the product rule to differentiate \(x\ln x\)
Work out \(\large\int{x \sin x^2\cdot e^{\cos x^2}{dx}}\)
This is an integration by recognition question in the form \(\large\int{f'(x)e^{f(x)}{dx}}=e^{f(x)}+C\)
We can also use integration by substitution with the substitution \(u=\cos x^2\)
We use the chain rule to differentiate \(\cos x^2\)
Here is a quiz that practises Integration by Recognition in the form \(\large \int f'(x)[f(x)]^{n} {d x}\)
START QUIZ!
Integration by recognition 2 1/1
Work out \(\large \int 2x(x^2+1)^3 {d x}\)
This is an integration by recognition question in the form \(\large \int f'(x)[f(x)]^{n} {d x}=\frac{[f(x)]^{n+1}}{n+1}+C\)
We can also use integration by substitution using the substitution \(\large u=x^2+1\)
Work out \(\large \int e^x(e^x+1)^2 {d x}\)
This is an integration by recognition question in the form \(\large \int f'(x)[f(x)]^{n} {d x}=\frac{[f(x)]^{n+1}}{n+1}+C\)
We can also use integration by substitution using the substitution \(\large u=e^x+1\)
Work out \(\large \int \cos x\sin ^2x \ {d x}\)
This is an integration by recognition question in the form \(\large \int f'(x)[f(x)]^{n} {d x}=\frac{[f(x)]^{n+1}}{n+1}+C\)
We can also use integration by substitution using the substitution \(\large u=\sin x\)
Work out \(\large \int \frac{(\ln x+1)^2}{x} {d x}\)
This is an integration by recognition question in the form \(\large \int f'(x)[f(x)]^{n} {d x}=\frac{[f(x)]^{n+1}}{n+1}+C\)
We can also use integration by substitution using the substitution \(\large u=\ln x+1\)
Work out \(\large \int 9x^2(x^3+3)^2{d x}\)
This is an integration by recognition question in the form \(\large \int f'(x)[f(x)]^{n} {d x}=\frac{[f(x)]^{n+1}}{n+1}+C\)
We can also use integration by substitution using the substitution \(\large u=x^3+3\)
Work out \(\large \int \frac{2x}{(x^2+1)^2}{d x}\)
This is an integration by recognition question in the form \(\large \int f'(x)[f(x)]^{n} {d x}=\frac{[f(x)]^{n+1}}{n+1}+C\)
It helps if we think about the question to be \(\large \int \frac{2x}{(x^2+1)^2}{d x}=\int 2x(x^2+1)^{-2}{d x}\)
We can also use integration by substitution using the substitution \(\large u=x^2+1\)
Work out \(\large \int \frac{e^x}{(e^x-1)^3}{d x}\)
This is an integration by recognition question in the form \(\large \int f'(x)[f(x)]^{n} {d x}=\frac{[f(x)]^{n+1}}{n+1}+C\)
It helps if we think about the question to be \(\large \int \frac{e^x}{(e^x-1)^3}{d x}=\int e^x(e^x-1)^{-3}{d x}\)
We can also use integration by substitution using the substitution \(\large u=e^x-1\)
Work out \(\large \int 2x\sqrt{x^2+1}{d x}\)
This is an integration by recognition question in the form \(\large \int f'(x)[f(x)]^{n} {d x}=\frac{[f(x)]^{n+1}}{n+1}+C\)
It helps if we think about the question to be \(\large \int 2x\sqrt{x^2+1}{d x}=\large \int 2x(x^2+1)^{\frac{1}{2}}{d x}\)
We can also use integration by substitution using the substitution \(\large u=x^2+1\)
Work out \(\large \int 3{\cos x\sqrt{\sin x}}{d x}\)
This is an integration by recognition question in the form \(\large \int f'(x)[f(x)]^{n} {d x}=\frac{[f(x)]^{n+1}}{n+1}+C\)
It helps if we think about the question to be \(\large \int 2{\cos x\sqrt{\sin x}}{d x}= 3\int \cos x(\sin x)^{\frac{1}{2}}{d x}\)
We can also use integration by substitution using the substitution \(\large u=\sin x\)
Work out \(\large \int \frac{\cos 2x}{\sqrt{1-\sin 2x}}{d x}\)
This is an integration by recognition question in the form \(\large \int f'(x)[f(x)]^{n} {d x}=\frac{[f(x)]^{n+1}}{n+1}+C\)
It helps if we think about the question to be \(\large \int \frac{\cos 2x}{\sqrt{1-\sin 2x}}{d x}=\int \cos 2x(1-\sin 2x)^{-\frac{1}{2}}{d x}\)
We can also use integration by substitution using the substitution \(\large u=1-\sin 2x\)
Here's a quiz that practises Integration by Substitution
START QUIZ!
Mixed SL Integration 2 1/1
Work out \(\int { x{ e }^{ x² }dx } \)
We can use integration by substitution. Let u = x²
| \(\int { x{ e }^{ x² }dx } \) | |
| \(u=x²\\ \frac { du }{ dx } =2x\\ \frac { 1 }{ 2 } du=xdx\) | |
| \(\int { { e }^{ u }\frac { 1 }{ 2 } du } \) | |
| \(=\frac { 1 }{ 2 } \int { { e }^{ u }du } \) | |
| \(=\frac { 1 }{ 2 } { e }^{ u }+C\) | |
| \(=\frac { 1 }{ 2 } { e }^{ x² }+C\) | |
Work out \(\int { { e }^{ x }{ \left( { e }^{ x }+1 \right) }^{ 3 }dx } \)
We can use integration by substitution. Let \(u={ e }^{ x }+1\)
| \(\int { { e }^{ x }{ \left( { e }^{ x }+1 \right) }^{ 3 }dx } \) | |
| \(u={ e }^{ x }+1\\ \frac { du }{ dx } ={ e }^{ x }\\ du={ e }^{ x }dx\) | |
| \(\int { { u }^{ 3 }du } \) | |
| \(=\frac { { u }^{ 4 } }{ 4 } +C\) | |
| \(=\frac { { \left( { e }^{ x }+1 \right) }^{ 4 } }{ 4 } +C\) | |
Work out \(\int { x\sqrt { x^{ 2 }+1 } dx } \)
We can use integration by substitution. Let u = x²+1
| \(\int { x\sqrt { x^{ 2 }+1 } dx } \) | |
\(u=x^2+1 \\ \frac { du }{ dx } =2x \\ \frac{1}{2}du=xdx\) | |
| \(\int { \sqrt { u }\cdot \frac{1}{2}du } \) | |
| \(=\frac { 1 }{ 2 } \int { { u }^{ \frac { 1 }{ 2 } }du } \) | |
| \(=\frac { 1 }{ 2 } \frac { { u }^{ \frac { 3 }{ 2 } } }{ \frac { 3 }{ 2 } } +C\) | |
| \(=\frac { { u }^{ \frac { 3 }{ 2 } } }{ 3 } +C\) | |
| \(=\frac { { (x²+1) }^{ \frac { 3 }{ 2 } } }{ 3 } +C\) |
Work out \(\int { { e }^{ x }sin\left( { e }^{ x } \right) dx } \)
We can use integration by substitution. Let \(u={ e }^{ x }\)
| \(\int { { e }^{ x }sin\left( { e }^{ x } \right) dx } \) | |
| \(u={ e }^{ x }\\ \frac { du }{ dx } ={ e }^{ x }\\ du={ e }^{ x }dx\) | |
| \(\int { sinudu } \) | |
| \(=-cosu+C\) | |
| \(=-cos({ e }^{ x })+C\) | |
Work out \(\int { \frac { 2x+3 }{ x²+3x } dx } \)
We can use integration by substitution. Let \(u=x²+3x\)
| \(\int { \frac { 2x+3 }{ x²+3x } dx } \) | |
| \(u=x²+3x\\ \frac { du }{ dx } =2x+3\\ du=\left( 2x+3 \right) dx\) | |
| \(\int { \frac { 1 }{ u } du } \) | |
| \(=ln|u|+C\) | |
| \(=ln|x²+3x|+C\) |
Work out \(\int { cosxsin²xdx } \)
We can use integration by substitution. Let \(u=sinx\)
| \(\int { cosxsin²xdx } \) | |
| \(u=sinx\\ \frac { du }{ dx } =cosx\\ du=cosxdx\) | |
| \(\int { u²du } \) | |
| \(=\frac { { u }^{ 3 } }{ 3 } +C\) | |
| \(=\frac { sin^{ 3 }x }{ 3 } +C\) |
Work out \(\int { \frac { cosx }{ sinx } dx } \)
We can use integration by substitution. Let \(u=sinx\)
| \(\int { \frac { cosx }{ sinx } dx } \) | |
| \(u=sinx\\ \frac { du }{ dx } =cosx\\ du=cosxdx\) | |
| \(\int { \frac { 1 }{ u } du } \) | |
| \(=ln|u|+C\) | |
| \(=ln|sinx|+C\) |
Work out \(\int { \frac { lnx }{ x } dx } \)
We can use integration by substitution. Let \(u=lnx\)
| \(\int { \frac { lnx }{ x } dx } \) | |
| \(u=lnx\\ \frac { du }{ dx } =\frac { 1 }{ x } \\ du=\frac { 1 }{ x } dx\) | |
| \(\int { udu } \) | |
| \(=\frac { { u }^{ 2 } }{ 2 } +C\) | |
| \(=\frac { { \left( lnx \right) }^{ 2 } }{ 2 } +C\) |
Work out \(\int { \frac { { e }^{ \sqrt { x } } }{ \sqrt { x } } dx } \)
We can use integration by substitution. Let \(u={ x }^{ \frac { 1 }{ 2 } }\)
| \(\int { \frac { { e }^{ \sqrt { x } } }{ \sqrt { x } } dx } \) | |
| \(u={ x }^{ \frac { 1 }{ 2 } }\\ \frac { du }{ dx } =\frac { 1 }{ 2 } { x }^{ -\frac { 1 }{ 2 } }\\ \frac { du }{ dx } =\frac { 1 }{ 2 } \frac { 1 }{ \sqrt { x } } \\ 2du=\frac { 1 }{ \sqrt { x } } dx\) | |
| \(2\int { { e }^{ u }dx } \) | |
| \(=2{ e }^{ u }+C\) | |
| \(=2{ e }^{ \sqrt { x } }+C\) |
Work out \(\int { { cos }^{ 3 }xdx } \)
This question becomes more obvious if we re-write the integrand
\(\int { { cos }^{ 3 }xdx } =\int { { cosxcos }^{ 2 }xdx } \)
Use a Pythagorean Trig Identity to write cos²x in terms of sin²x
\(=\int { { cosx(1-sin }^{ 2 }x)dx } \)
Now, we can use integration by substitution. Let \(u=sinx\)
| \(\int { { cosx(1-sin }^{ 2 }x)dx } \) | |
| \(u=sinx\\ \frac { du }{ dx } =cosx\\ du=cosxdx\) | |
| \(\int { (1-u²)du } \) | |
| \(=u-\frac { { u }^{ 3 } }{ 3 } +C\) | |
| \(=sinx-\frac { sin^{ 3 }x }{ 3 } +C\) |
Here's a quiz that practises Definite Integration
START QUIZ!
Mixed SL Integration 3 1/1

Answer =
\({ \left[ \frac { -cos2x }{ 2 } \right] }_{ \frac { \pi }{ 4 } }^{ \frac { \pi }{ 2 } }\)
\(=\frac { -cos\pi }{ 2 } -\frac { -cos\left( \frac { \pi }{ 2 } \right) }{ 2 } \)
\(=-\frac { -1 }{ 2 } -0\)
\(\int _{ -1 }^{ 1 }{ \frac { 1 }{ x+2 } dx } =lnk\)
Work out the value of k
k =
\({ \left[ ln|x+2| \right] }_{ -1 }^{ 1 }\)
\(=ln|3|-ln|1|\)
\(=ln3\)

Answer =
\(\int _{ 1 }^{ 4 }{ \frac { 1 }{ \sqrt { x } } dx } =\int _{ 1 }^{ 4 }{ { x }^{ -0.5 }dx } \)
\( ={ \left[ \frac { { x }^{ 0.5 } }{ 0.5 } \right] }_{ 1 }^{ 4 }\)
\(={ \left[ 2\sqrt { x } \right] }_{ 1 }^{ 4 }\)
\(=2\sqrt { 4 } -2\sqrt { 1 } \)
= 4 - 2 = 2
\(\int _{ -2 }^{ 0 }{ \frac { 1 }{ { e }^{ 2x } } dx } =\frac { { e }^{ a }-1 }{ 2 } \)
Work out the value of a
a =
\(\int _{ -2 }^{ 0 }{ \frac { 1 }{ { e }^{ 2x } } dx } =\int _{ -2 }^{ 0 }{ { e }^{ -2x }dx } \)
\(={ \left[ \frac { { e }^{ -2x } }{ -2 } \right] }_{ -2 }^{ 0 }\)
\(=\frac { { -e }^{ 0 } }{ 2 } -\frac { { -e }^{ 4 } }{ 2 }\)
\( =-\frac { 1 }{ 2 } +\frac { { e }^{ 4 } }{ 2 } \)
\(=\frac { { e }^{ 4 }-1 }{ 2 } \)
Work out \(\int _{ 0 }^{ \frac { \pi }{ 6 } }{ cosx{ e }^{ sinx }dx } \)
This question requires integration by substitution. Let = sinx
| \(\int _{ 0 }^{ \frac { \pi }{ 6 } }{ cosx{ e }^{ sinx }dx } \) | |
| \(u=sinx\\ \frac { du }{ dx } =cosx\\ du=cosxdx\) | |
| \(\int _{ 0 }^{ \frac { \pi }{ 6 } }{ cosx{ e }^{ sinx }dx } \) | |
| Change the limits using the substitution | |
| \(=\int _{ sin0 }^{ sin\frac { \pi }{ 6 } }{ { e }^{ u }du } \) | |
| \(={ [{ e }^{ u }] }_{ 0 }^{ 0.5 }\) | |
| \(={ e }^{ 0.5 }-{ e }^{ 0 }\) | |
| \(=\sqrt { e } -1\) |
\(\int _{ e }^{ e² }{ \frac { 1 }{ xlnx } dx } =lna\)
Work out the value of a
a =
This question requires integration by substitution. Let = lnx
| \(\int _{ e }^{ e² }{ \frac { 1 }{ xlnx } dx } \) | |
| \(u=lnx\\ \frac { du }{ dx } =\frac { 1 }{ x } \\ du=\frac { 1 }{ x } dx\) | |
| \(=\int _{ lne }^{ lne² }{ \frac { 1 }{ u } du } \) | |
| \(=\int _{ 1 }^{ 2 }{ \frac { 1 }{ u } du } \) | |
| \(=[{ lnu] }_{ 1 }^{ 2 }\) | |
| \(=ln2-ln1\) | ln1 = 0 |
| \(=ln2\) |
Which of the following are true?
Select ALL correct answers
There are two incorrect answers. We could be confusing them with the following correct properties of the definite integral
- \(2\int _{ 1 }^{ 2 }{ f(x)dx } =\int _{ 1 }^{ 2 }{2 f(x)dx } \)
- \(\int _{ 1 }^{ 3 }{ f(x)dx } =\int _{ 2 }^{ 3 }{ f(x)dx } +\int _{ 1 }^{2 }{ f(x)dx } \)
Which of the following are true?
Select ALL correct answers
Note that lnx²=2lnx
\(\int _{ 0 }^{ 2 }{ [x+f(x)]dx } \\ =\int _{ 0 }^{ 2 }{ xdx } +\int _{ 0 }^{ 2 }{ f(x)dx } \\ ={ \left[ \frac { x² }{ 2 } \right] }_{ 0 }^{ 2 }+\int _{ 0 }^{ 2 }{ f(x)dx } \\ =2+\int _{ 0 }^{ 2 }{ f(x)dx } \)
The graph below shows the function f
Evaluate the following definite integral
\(\int _{ 3 }^{ -1 }{ f(x)dx } \) =
\(\int _{ -1 }^{ 3 }{ f(x)dx } \) represents the following definite integral
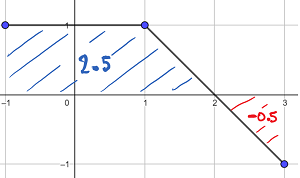
Therefore, \(\int _{ -1 }^{ 3 }{ f(x)dx } =2\)
So, \(\int _{ 3}^{ -1 }{ f(x)dx } =-2\)
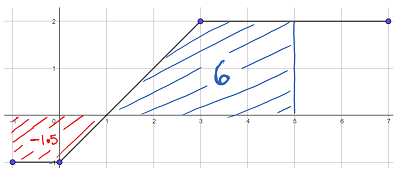
The graph shows the function f
\(\int _{ -1 }^{ a }{ f(x)dx } =4.5\)
Find the value of a
a =
The graph below shows that the definite integral \(\int _{ -1 }^{ 5 }{ f(x)dx } =4.5\)
Here's a quiz that practises Areas between Graphs
START QUIZ!
Mixed SL Integration 4 1/1
The two functions, f and g are
f(x) = cos²x
g(x) = cos2x
Which one of the following will give the area of the region shaded below
f(x) = cos²x is the upper curve
We need to find the area under f and then subtract the area under g
Let \(f(x)=e^{x-1}\)
The diagram below shows the graph of y = f(x) and the tangent at the point x = 1
Which of the following gives the area of the shaded region
We need to find the area under the curve and subtract the area under the tangent (the triangle).
The area under the curve = \(\int _{ 0 }^{ 1 }{ f(x)dx }\)
The height of the triangle is \(f(1)=e^0=1\)
The area of the triangle = \(\frac{1\times1}{2}=0.5\)
Hence the shaded area = \(\int _{ 0 }^{ 1 }{ f(x)dx } -0.5\)

Area =
The area of the region can be found by working out the following integral
\(\int _{ 1 }^{ e }{ \frac { 1 }{ x } dx={ [ln|x|] }_{ 1 }^{ e } } \)
= lne - ln1
= 1 - 0
=1
The area of the region bounded by the graph \(y = \frac{1}{2x}\), x = a, x = 1 and the x axis is equal to \(ln3\)
Work out the value of a
a =
\(\int _{ 1 }^{ a }{ \frac { 1 }{ 2x } dx } \)
\(=\frac { 1 }{ 2 } \int _{ 1 }^{ a }{ \frac { 1 }{ x } dx } \)
\(=\frac { 1 }{ 2 } { [ln|x|] }_{ 1 }^{ a }\)
\(=\frac { 1 }{ 2 } (lna-ln1)\)
\(=\frac { 1 }{ 2 } lna\)
\(=ln{ a }^{ \frac { 1 }{ 2 } }\)
\(ln{ a }^{ \frac { 1 }{ 2 } }=ln3 \\ { a }^{ \frac { 1 }{ 2 } }=3 \\a=9\)

The area of the shaded region = \(\frac{a}{3}\)
Find the value of a
a =
Area = \(\int _{ -1 }^{ 1 }{ (2-x²)dx } -\int _{ -1 }^{ 1 }{ x²dx } \)
We can put the two integrals together
Area = \(\int _{ -1 }^{ 1 }{ (2-x²-x²)dx } \)
\(=\int _{ -1 }^{ 1 }{ (2-2x²)dx } \)
\(={ \left[ 2x-\frac { 2{ x }^{ 3 } }{ 3 } \right] }_{ -1 }^{ 1 }\)
\(=\left[ 2-\frac { 2 }{ 3 } \right] -\left[ -2+\frac { 2 }{ 3 } \right] \)
\(=\frac{8}{3}\)
The diagram below shows the graphs of y = sinx and y = cosx.
The area of the shaded region = \(a\sqrt{2}\)
Find the value of a
a =
Area = \(\int _{ \frac { \pi }{ 4 } }^{ \frac { 5\pi }{ 4 } }{ sinxdx } -\int _{ \frac { \pi }{ 4 } }^{ \frac { 5\pi }{ 4 } }{ cosxdx } \)
We can put the two integrals together
Area = \(\int _{ \frac { \pi }{ 4 } }^{ \frac { 5\pi }{ 4 } }{ (sinx-cosx)dx } \)
\(={ \left[ -cosx-sinx \right] }_{ \frac { \pi }{ 4 } }^{ \frac { 5\pi }{ 4 } }\)
\(=\left[ -cos\frac { 5\pi }{ 4 } -sin\frac { 5\pi }{ 4 } \right] -\left[ -cos\frac { \pi }{ 4 } -sin\frac { \pi }{ 4 } \right] \)
\(=\left[ \frac { \sqrt { 2 } }{ 2 } +\frac { \sqrt { 2 } }{ 2 } \right] -\left[ -\frac { \sqrt { 2 } }{ 2 } -\frac { \sqrt { 2 } }{ 2 } \right] \)
\(=\left[ \sqrt { 2 } \right] -\left[ -\sqrt { 2 } \right] \)
\(=2\sqrt { 2 } \)

The graphs of y = f(x) and y = g(x) meet at x = 0 and x = \(\frac{\pi}{3}\) as shown below.
Find the area of the shaded region
Area =
Area = \(\int _{ 0 }^{ \frac { \pi }{ 3 } }{ (sin2x-sinx)dx } \)
\(={ \left[ -\frac { cos2x }{ 2 } +cosx \right] }_{ 0 }^{ \frac { \pi }{ 3 } }\)
\(=\left[ -\frac { cos\frac { 2\pi }{ 3 } }{ 2 } +cos\frac { \pi }{ 3 } \right] -\left[ -\frac { cos0 }{ 2 } +cos0 \right] \)
\(=\left[ \frac { 1 }{ 4 } +\frac { 1 }{ 2 } \right] -\left[ -\frac { 1 }{ 2 } +1 \right] \)
\(=\frac { 1 }{ 4 } \)
The diagram below shows the graph of \(y = \frac{2x}{x^2-1}\)
The shaded region has an area \(lna\)
Find the value of a
a =
Area = \(\int _{ 2 }^{ 4 }{ \frac { 2x }{ x²-1 } dx } \)
We might recognise that this integral is in the form \(=\int { \frac { f'(x) }{ f(x) } dx=ln|f(x)|+C } \)
Or, we could use Integration by substitution with the substitution u = x² - 1
\(\int _{ 2 }^{ 4 }{ \frac { 2x }{ x²-1 } dx } ={ \left[ ln|x²-1| \right] }_{ 2 }^{ 4 }\)
= ln 15 - ln 3
\(=ln\frac { 15 }{ 3 } \)
= ln3
Here's a quiz that practises Kinematics
START QUIZ!
Mixed SL Integration 5 1/1
A rocket starts from rest and accelerates such that \(a(t)=3t+t^2\), where t = time
Find a formula for the velocity of the rocket at time t
In order to find velocity, we need to integrate the acceleration formula
\(v(t)=\int { (3t+t^{ 2 })dt } \\ =\frac { 3t^{ 2 } }{ 2 } +\frac { { t }^{ 3 } }{ 3 } +C\)
The rocket starts from rest, so when t = 0, v = 0
\(0=\frac { 3(0^{ 2 }) }{ 2 } +\frac { { 0 }^{ 3 } }{ 3 } +C\)
C = 0
\(v(t) =\frac { 3t^{ 2 } }{ 2 } +\frac { { t }^{ 3 } }{ 3 } \)

Find the displacement of the object relative to its initial position at \(t=\frac{3\pi}{2}\)
displacement =
To find displacement, we find the definite integral of velocity
\(s(t)=\int _{ 0 }^{ \frac { 3\pi }{ 2 } }{ -2sintdt } \)
\(={ \left[ 2cost \right] }_{ 0 }^{ \frac { 3\pi }{ 2 } }\)
\(=\left[ 2cos\left( \frac { 3\pi }{ 2 } \right) \right] -\left[ 2cos0 \right] \)
= 0 - 2
= -2
The object has travelled backwards and is behind its initial position.

The velocity-time graph below shows the velocity of an object in the first 3 seconds.
\(v(t) = 2tsin(t^2)\)
Find the distance travelled in the first \(\sqrt{2\pi}\) seconds
Distance travelled = m
In order to integrate the function, we can use integration by substitution with the substitution u = t²
| \(\int { 2tsin(t²)dt } \) | |
| \(u=t²\\ \frac { du }{ dt } =2t\\ du=2tdt\) | |
| \(\int { sinudu } \) | |
| \(=-cosu+C\) | |
| \(=-cos(t²)+C\) |
You might understand from the graph that the object travels backwards first.
If we find the definite integral from 0 to \(\sqrt{2\pi}\), this will find the displacement of the object relative from the starting position. The WRONG answer!
The distance travelled is given by the area under the graph.
We need to split the area into 2 parts
| \(\int _{ 0 }^{ \sqrt { \pi } }{ 2tsin(t²)dt } \\ =\int _{ 0 }^{ \pi }{ sinudu } \\ ={ \left[ -cosu \right] }_{ 0 }^{ \pi }\\ =\left[ -cos(\pi ) \right] -\left[ -cos(0) \right] \\ =1+1\\ =2\) | \(\int _{ \sqrt { \pi } }^{ \sqrt { 2\pi } }{ 2tsin(t²)dt } \\=\int _{ \pi }^{ 2\pi }{ sinudu } \\={ \left[ -cosu \right] }_{ \pi }^{ 2\pi }\\=\left[ -cos(2\pi ) \right] -\left[ -cos(\pi ) \right]\\ =-1-1\\=-2\) |
Distance travelled in the first part = 2
Distance travelled in the second part = 2
Total distance = 4

\(v(t)=3sint-t^{cost}\), for 0 ≤ t ≤ 6
Find the displacement after 6 seconds to 3 significiant figures
Displacement =
Use your calculator to find the definite integral \(\int _{ 0 }^{ 6 }{ (3sint-t^{ cost })dt } \)

\(v(t)=\sqrt{t}cos(\frac{πt}{4})\)
Find the total distance travelled in the first 6 seconds.
Total distance travelled =
You might understand from the graph that the object travels forwards first then backwards.
If we find the definite integral from 0 to 6, this will find the displacement of the object relative from the starting position. The WRONG answer!
The distance travelled is given by the area under the graph.
Use your graphical calculator to find the total area
\(\int _{ 0 }^{ 2 }{ \sqrt { t } cos(\frac { πt }{ 4 } )dt } \approx 1.011\\ \int _{ 2 }^{ 6 }{ \sqrt { t } cos(\frac { πt }{ 4 } )dt } \approx -5.062\)
Area \(\approx 1.01+5.06\approx6.07\)
Here's a quiz that practises Volumes of Revolution
START QUIZ!
Mixed SL Integration 6 1/1
The shaded region is rotated 360° about the x axis.
Which of the following will find the volume of the solid formed?
Find
the volume formed by g
then subtract the volume formed by f
Let f(x) =lnx and g(x) = 2ln(x - 2)
The graphs of f and g are shown below.
The shaded region is rotated 360° about the x axis.
Which of the following will find the volume of the solid formed?
The graph in black is f(x) =lnx
The graph in blue is g(x) = 2ln(x - 2)
Consider a region under each function
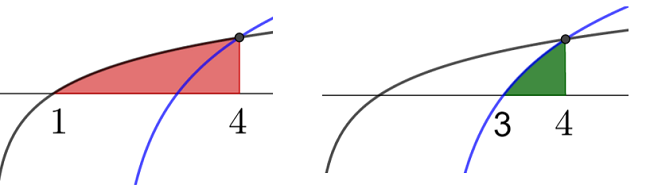
We can see that we need to work out \(\pi \int _{ 1 }^{ 4 }{ { \left[ f(x) \right] }^{ 2 }dx } -\pi \int _{ 3 }^{ 4 }{ { \left[ g(x) \right] }^{ 2 }dx } \)
\(=\pi \int _{ 1 }^{ 4 }{ { \left[ lnx \right] }^{ 2 }dx } - \pi \int _{ 3 }^{ 4 }{ { \left[ 2ln(x-2) \right] }^{ 2 }dx } \)

The region enclosed by the graph of f and the x axis is rotated 360° around the x axis.
The volume of the the solid formed is \(\frac{a}{35}\pi\).
Find the value of a
a =
You can use your graphical calculator for this question.
If we were calculating the area, we would have to split this into 2 separate integrals, but this is not necessary for volumes (this is no negative value)
Volume = \(\pi\int _{ -1 }^{ 3 }{ { \left[ (f(x) \right] }^{ 2 }dx } \)
\( =\pi\int _{ -1 }^{ 3 }{ { \left[ (x+1)(x-1)(x-3) \right] }^{ 2 }dx } \\ =\frac { 162 }{ 35 } \pi \\ \approx 14.5\)

The graph of f has a minimum value at x = a
The shaded region is rotated 360° around the x axis. Find the volume of the solid formed.
Give your answer to 3 significant figures.
Volume \(\approx\)
This is a question for your graphical calculator.
We can find the x coordinate of A (minimum point). It is best to find this to 4 significant figures.
-0.6214
We also need to find the x coordinate of B (x intercept)
1
The volume is found by calculating \(\pi\int _{ -0.6214}^{ 1 }{ { \left[ f(x) \right] }^{ 2 }dx } \)
Don't forget \(\pi\)
On your calculator, work out \(\pi\int _{ -0.6214 }^{ 1 }{ { \left[ 3xln(2-x^{ 2 }) \right] }^{ 2 }dx } \) and round it to 3 significant figures

The volume of the solid generated by rotatring R 360° around the x axis is given by \(a\pi\).
Find the value of a
a =
Volume = \(\pi \int _{ 1 }^{ 2 }{ { \left[ (f(x) \right] }^{ 2 }dx } \)
\(=\pi \int _{ 1 }^{ 2 }{ { \left[ \frac { 4 }{ x } \right] }^{ 2 }dx } \)
\(=\pi \int _{ 1 }^{ 2 }{ { 16 }{ x }^{ -2 }dx } \)
\(=\pi { \left[ -16{ x }^{ -1 } \right] }_{ 1 }^{ 2 }\)
\(=\pi \left[ -\frac { 16 }{ x } \right] _{ 1 }^{ 2 }\)
\(=\pi [-8+16]\)
\(=8\pi \)

The shaded region is rotated 360° around the x axis and the volume of the solid created is \(\frac{a\pi}{3}\)
Work out the value of a
a =
The solid is made up of 2 parts
- the region formed by the curve
- the cone formed by the straight line
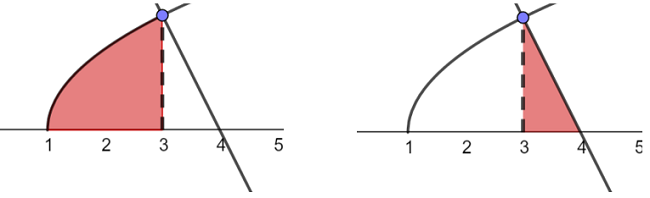
Volume = \(\pi \int _{ 1 }^{ 3 }{ { (2x-2) }dx } +\frac { 1 }{ 3 } \pi \cdot { 2 }^{ 2 }\cdot 1\)
\(=\pi { \left[ x^{ 2 }-2x \right] }_{ 1 }^{ 3 }+\frac { 4\pi }{ 3 } \)
\(=\pi { \left[ 9-6 \right] }-\pi { \left[ 1-2 \right] }+\frac { 4\pi }{ 3 } \)
\(=4\pi +\frac { 4\pi }{ 3 } \)
\(=\frac { 16\pi }{ 3 } \)
text
You can get further practice by trying a dynamic quiz.
If you refresh this page, you will get a new set of quizzes
The following integral can be performed by using integration by substitution (or U-substitution). Which is the correct substitution?
\(\int { sin^2x \ cosx \ dx } \)
If u = sinx
then \(\frac { du }{ dx } =cosx\)
Integrand becomes \(\int { { u }^{ 2 }du } \)
The graph below shows the function f
Evaluate the following definite integral

\(\int _{ -1 }^{ 0 }{ f(x)dx } \) =
 definite integral is negative as it is below x axis
definite integral is negative as it is below x axis
The graph below shows the function f
\(\int _{ a }^{ 7 }{ f(x)dx } =0\)
Find 2 possible values of a , a1 and a2
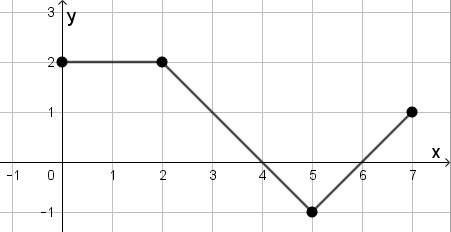
You must choose a value for a that makes the definite integral from a to 7 equal 0.
Choose a value of a, so that the area of the region below the x axis must equal the area above the x axis.
A rocket starts from rest and accelerates such that \(a(t)=3t+t^2\), where t = time
Find a formula for the velocity of the rocket at time t
In order to find velocity, we need to integrate the acceleration formula
\(v(t)=\int { (3t+t^{ 2 })dt } \\ =\frac { 3t^{ 2 } }{ 2 } +\frac { { t }^{ 3 } }{ 3 } +C\)
The rocket starts from rest, so when t = 0, v = 0
\(0=\frac { 3(0^{ 2 }) }{ 2 } +\frac { { 0 }^{ 3 } }{ 3 } +C\)
C = 0
\(v(t) =\frac { 3t^{ 2 } }{ 2 } +\frac { { t }^{ 3 } }{ 3 } \)
Work out \(\large\int\frac{2x}{x^2+1} \mathrm{d}x\)
\(\frac{\mathrm{d}}{\mathrm{d}x}(x^2+1)=2x\)
Hence integral is in the form \(\int\frac{f'(x)}{f(x)} \mathrm{d}x=\ln |f(x)|+C\)
\(\int\frac{2x}{x^2+1} \mathrm{d}x=\ln |x^2+1|+C\)
Given that \(\int _{ -2 }^{ 2 }{ f(x)dx=5 } \) and \(\int _{ -2 }^{ 0 }{ f(x)dx=3 } \) work out
a) \(\int _{ 0 }^{ 2 }{ 2f(x)dx } \) =
b) \(\int _{ 2 }^{ 4 }{ f(x-2)dx } \) =
c) \(\int _{ -2 }^{ 2 }{ (f(x)+2)dx } \) =
a) Consider the same definite integral split into two parts
\(\int _{ -2 }^{ 0 }{ f(x)dx}+\int _{ 0 }^{ 2 }{ f(x)dx } =\int _{ -2 }^{ 2 }{ f(x)dx } \\3 + 2 = 5\\\int _{ 0 }^{ 2 }{ f(x)dx }=2\)
b) f(x - 2) translates the graph of f(x) 2 units to the right. This is the same as \(\int _{ 0 }^{ 2 }{ f(x)dx } \)
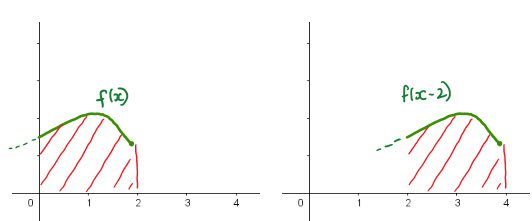
c) f(x) + 2 translates the graph 2 units up. It creates a region the same as \(\int _{ -2 }^{ 2 }{ f(x)dx=5 } \) , but with a rectangle below. The area of the rectangle is 8.

Work out \(\int { \frac { lnx }{ x } dx } \)
We can use integration by substitution. Let \(u=lnx\)
| \(\int { \frac { lnx }{ x } dx } \) | |
| \(u=lnx\\ \frac { du }{ dx } =\frac { 1 }{ x } \\ du=\frac { 1 }{ x } dx\) | |
| \(\int { udu } \) | |
| \(=\frac { { u }^{ 2 } }{ 2 } +C\) | |
| \(=\frac { { \left( lnx \right) }^{ 2 } }{ 2 } +C\) |
The diagram below shows the graph of \(y = \frac{2x}{x^2-1}\)
The shaded region has an area \(lna\)
Find the value of a
a =
Area = \(\int _{ 2 }^{ 4 }{ \frac { 2x }{ x²-1 } dx } \)
We might recognise that this integral is in the form \(=\int { \frac { f'(x) }{ f(x) } dx=ln|f(x)|+C } \)
Or, we could use Integration by substitution with the substitution u = x² - 1
\(\int _{ 2 }^{ 4 }{ \frac { 2x }{ x²-1 } dx } ={ \left[ ln|x²-1| \right] }_{ 2 }^{ 4 }\)
= ln 15 - ln 3
\(=ln\frac { 15 }{ 3 } \)
= ln3
Work out \(\large\int\frac{1}{x\ln x} \mathrm{d}x\)
\(\int\frac{1}{x\ln x} \mathrm{d}x=\int\frac{\frac{1}{x}}{\ln x} \mathrm{d}x\)
\(\frac{\mathrm{d}}{\mathrm{d}x}(\ln x)=\frac{1}{x}\)
Hence integral is in the form \(\int\frac{f'(x)}{f(x)} \mathrm{d}x=\ln |f(x)|+C\)
\(\int\frac{\frac{1}{x}}{\ln x} \mathrm{d}x=\ln|\ln x|+C\)
Work out \(\large \int_0^{1} \frac {x(e^{x^2}+1)}{e^{x^2}+x^2} {d x}\)
This is an integration by recognition question in the form \(\large \int \frac {f'(x)}{f(x)} {d x}=\ln |f(x)|+C\)
We can also use integration by substitution using the substitution \(\large u=\cos x\)
Note that, \(\large \frac{d}{dx}(e^{x^2}+x^2)=2xe^{x^2}+2x=2x(e^{x^2}+1)\)
So, we have
\(\large \frac{1}{2}\int_0^{1} \frac {2x(e^{x^2}+1)}{e^{x^2}+x^2} {d x}=\frac{1}{2}[\ln |e^{x^2}+x^2|]_0^{1}\\ \large =\frac{1}{2}\ln([e^1+1]-[e^0+0]) \\ \large=\frac{1}{2}\ln\frac{e+1}{1}\\ \large=\frac{1}{2}\ln(e+1)\)
How much of Mixed Integration have you understood?
Feedback
Which of the following best describes your feedback?


 Medium
Medium Hard
Hard Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn