Find an expression for $\frac{dC}{dx}$ in terms of $k$ and $x$.

Calculate the area of cloth, in cm², needed to make Haruka’s bag.

Use your answers to parts (c) and (d) to show that

$A=3x^2+\frac{10368}{x}$.

Find f "(x).

Find $g^{\prime }(-1)$.

Show that the normal to the curve at the point where $x=1$ is $2y-x+3=0$.

Calculate $\frac{\text{d}\theta }{\text{d}t}$ when $\theta =\frac{\pi }{3}$.

Find the value of $x$ which maximizes the volume of the box.

Find $f\text{'}\left(x\right)$.

Use your answer to part (a) to find the gradient of $L$.

Find $f\text{'}\left(x\right)$.

Solve $S\text{'}\left(x\right)=0$.

Express this volume in $\text{c}{\text{m}}^3$.

Find $P\left(x\right)$.

Find u.

Find f '(x).

Solve f '(x) = f "(x).

Find the equation of the tangent line to the graph of $y=f\left(x\right)$ at $x=2$. Give the equation in the form $ax+by+d=0$ where, $a$, $b$, and $d\in \mathbb{Z}$.

Find the point on the graph of $f$ at which the gradient of the tangent is equal to 6.

Calculate the volume, in cm³, of the bag.

Write down the number of possible solutions to the equation $f(x)=5$.

Given that y = 2x³ − 9x² + 12x + 2 = k has three solutions, find the possible values of k.

Given that there is a minimum value for C, find this minimum value in terms of $\pi$.

Hence or otherwise, find the obtuse angle formed by the tangent line to $f$ at $x=8$ and the tangent line to $f$ at $x=2$.

The cloth used to make Nanako’s bag costs 4 Japanese Yen (JPY) per cm².

Find the cost of the cloth used to make Nanako’s bag.

Sketch the curve for −1 < x < 3 and −2 < y < 12.

Find $f^{\prime }(x)$.

Find the inverse function $g^{-1}$ and state its domain.

Calculate the surface area of the box in cm².

(i)     Find the first three derivatives of $g(x)$.

(ii)     Given that $g^{(19)}(x)=\frac{k!}{(k-p)!}(x^{k-19})$, find $p$.

Find $h^{\prime }(8)$.

Given the design constraint that $l=\frac{150-2\mathrm{\pi }{r}^2}{\mathrm{\pi }r}$, show that $V=150r-\frac{2\mathrm{\pi }{r}^3}{3}$.

Write down the $x$-coordinates of these two points;

A teacher asks her students to make some observations about the curve.

Three students responded.
Nadia said “The x-intercept of the curve is between −1 and zero”.
Rick said “The curve is decreasing when x < 1 ”.
Paula said “The gradient of the curve is less than zero between x = 1 and x = 2 ”.

State the name of the student who made an incorrect observation.

Write down the $y$-intercept of the graph.

(i)     Find $h^{\prime }(x)$.

(ii)     Hence, show that $h^{\prime }(\pi )=\frac{-21!}{2}{\pi }^2$.

Find the coordinates of P and Q.

Write down the derivative of $f$.

Hence justify that $g$ is decreasing at $x=-1$.

The folium of Descartes is a curve defined by the equation $x^3+y^3-3xy=0$, shown in the following diagram.

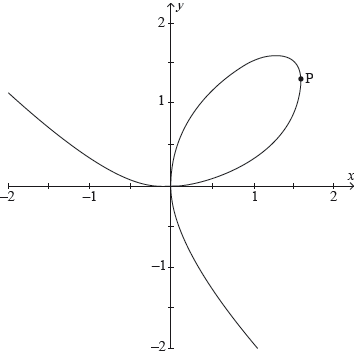
Determine the exact coordinates of the point P on the curve where the tangent line is parallel to the $y$-axis.

Find the value of $r$ when the area of the curved surface is maximized.

Using your answer to part (d), show that $V$ is a maximum when $r$ is equal to $\sqrt{\frac{75}{\mathrm{\pi }}} \text{cm}$.

Use your answer to part (f) to identify the shape of the speaker with the best quality of sound.

Find $f(2)$.

Find $\left(f\circ f\right)\left(x\right)$.

Find $\frac{\text{d}A}{\text{d}x}$.

Write down the value of $k$.

Find the x-coordinate of the point at which the normal to the graph of f has gradient $-\frac{1}{8}$.

Calculate the maximum value of $V$.

Find the acute angle between $y=x$ and $L$.

Hence, find the equation of L in terms of $a$.

Find the coordinates of P.

Find an expression for $\frac{\text{d}y}{\text{d}x}$ in terms of $x$ and $y$.

Write down and simplify an expression in x and y for the area of cloth, A, used to make Nanako’s bag.

Explain why $f$ is an even function.

Let $f(x)=(x^2+3{)}^7$. Find the term in $x^5$ in the expansion of the derivative, $f^{\prime }(x)$.

Find the value of $P$ if no vases are sold.

Find the length of the cylinder for which $V$ is a maximum.

Use your answer to part (f) to show that the width of Nanako’s bag is 12 cm.

Show that $a=8$.

Find $\frac{\text{d}V}{\text{d}r}$.

Find $f^{\prime }\left(x\right)$.

Find f'(x)

Find the equations of the tangents to this curve at the points where the curve intersects the line $x=1$.

Find the coordinates of the three points on C, nearest the origin, where the tangent is parallel to the line $y=-x$.

The graph of $f$ has a local minimum at the point Q. The line L passes through Q.

Find the value of $a$.

Write down an expression for $V$, the volume (cm³) of the speaker, in terms of $r$, $l$ and $\mathrm{\pi }$.

Expand the expression for $f(x)$.

Show that $k=-6$.

Hence, show that there are no solutions to $(g^{-1}{)}^{\prime }(x)=0$.

Find the equation of the tangent to the graph of $y=g(x)$ at $x=2$. Give your answer in the form $y=mx+c$.

Differentiate $P\left(x\right)$.

Write down the coordinates of the point of intersection.

Given that the gradients of the tangents to C at P and Q are m₁ and m₂ respectively, show that m₁ × m₂ = 1.

Write down the intervals where the gradient of the graph of $y=f(x)$ is positive.

Using your answer to part (e), find the value of $r$ which minimizes $A$.

Show that $\frac{\text{d}y}{\text{d}x}=-\left(\frac{1+y\text{sin}\left(xy\right)}{1+x\text{sin}\left(xy\right)}\right)$.

Use this value to write down, and simplify, the equation in x and y for the volume of Nanako’s bag.

Show that the equation of $L_1$ is $kx+p^{2}y-2pk=0$.

Write down the gradient of this tangent.

The equation $f(x)=m$, where $m\in \mathbb{R}$, has four solutions. Find the possible values of $m$.

Find $g^{\prime }(x)$.

Find $\frac{\text{d}A}{\text{d}r}$.

Use your answer to part (b)(ii) to find the values of $x$ for which $f$ is increasing.

Show that $C=20\pi r^2+\frac{320\pi }{r}$.

Find $\frac{\text{dy}}{\text{dx}}$.

Find the exact value of each of the zeros of $f$.

Find $f^{\prime }(x)$.

Find the least number of boxes which must be sold each week in order to make a profit.

Find $\frac{\text{d}y}{\text{d}x}$ in terms of $x$ and $y$.

Explain why the inverse function $f^{-1}$ does not exist.

Hence, show that there are no solutions to $g^{\prime }(x)=0$;

Show that $k=6$.

Find $g^{\prime }(x)$.

Find $f^{\prime }\left(x\right)$.

Write down the range of $f(x)$.

Find $f\text{'}\left(p\right)$ in terms of $k$ and $p$.

Find the value of $k$.

Find the coordinates of the local minimum.

Calculate the length AG.

Find an expression for the volume of water $V({\text{m}}^3)$ in the trough in terms of $\theta$.

Find $\frac{\text{d}y}{\text{d}x}$.

Find the coordinates of P.

Find the gradient of the graph of f at $x=-\frac{1}{2}$.

Find the $y$-coordinate of the local minimum.

Write down, in terms of $r$ and $h$, an equation for the volume of this water container.

Determine the equation of the tangent to $C$ at the point $\left(\frac{2}{\text{e}},\text{ e}\right)$

Draw the graph of $f$ for $-3⩽x⩽3$ and $-40⩽y⩽20$. Use a scale of 2 cm to represent 1 unit on the $x$-axis and 1 cm to represent 5 units on the $y$-axis.

Write down a formula for $A$, the surface area to be coated.

Find the least number of cans of water-resistant material that will coat the area in part (g).

Determine the equation of the normal at $x=-2$ in the form $y=mx+c$.

Find the gradient of $L$.

Hence, write down $f^{-1}\left(x\right)$.

Use your answer to part (a) and the value of $k$, to find the $x$-coordinates of the stationary points of the graph of $y=g(x)$.

Find $\frac{dy}{dx}$.

Show that $A=\pi r^2+\frac{1000000}{r}$.

Find the number of boxes that should be sold each week to maximize the profit.

Sketch the graph of $y=f(x)$ showing clearly the equations of asymptotes and the coordinates of any intercepts with the axes.

Write down an equation for the surface area of the speaker in terms of $r$, $l$ and $\mathrm{\pi }$.

The graph of $f$ is translated by $\left(\begin{array}{c}4\\ 3\end{array}\right)$ to give the graph of $g$.
In the following diagram:

• point $\text{Q}$ lies on the graph of $g$
• points $\text{C}$, $\text{D}$ and $\text{E}$ lie on the vertical asymptote of $g$
• points $\text{D}$ and $\text{F}$ lie on the horizontal asymptote of $g$
• point $\text{G}$ lies on the $x$-axis such that $\text{FG}$ is parallel to $\text{DC}$.

Line $L_2$ is the tangent to the graph of $g$ at $\text{Q}$, and passes through $\text{E}$ and $\text{F}$.

Given that triangle $\text{EDF}$ and rectangle $\text{CDFG}$ have equal areas, find the gradient of $L_2$ in terms of $p$.

Write down the interval where the gradient of the graph of $f\left(x\right)$ is negative.

Write down $f\prime \left(x\right)$.

Find the area of triangle $\text{AOB}$ in terms of $k$.

Find an expression for $\frac{dV}{dx}$.

Write down an equation for the area, $A$, of the curved surface in terms of $r$.

Find the largest possible domain $D$ for $f$ to be a function.

Find the value of this minimum area.

Find $\frac{\text{d}y}{\text{d}x}$.

Express h in terms of r.

Find $h(1)$.

Find an expression for $\frac{dy}{dx}$.

Hence find the values of θ for which $\frac{\text{d}y}{\text{d}\theta }=2y$.

Find $\frac{\text{d}y}{\text{d}\theta }$

Find the coordinates of the points on the curve $y^3+3x{y}^2-x^3=27$ at which $\frac{\text{d}y}{\text{d}x}=0$.

Find $\frac{\text{d}A}{\text{d}r}$.

Consider f(x), g(x) and h(x), for x∈$\mathbb{R}$ where h(x) = $\left(f\circ g\right)$(x).

Given that g(3) = 7 , g′ (3) = 4 and f ′ (7) = −5 , find the gradient of the normal to the curve of h at x = 3.

(i)     Find the first four derivatives of $f(x)$.

(ii)     Find $f^{(19)}(x)$.

Hence or otherwise find the minimum length of ribbon required.

Find the gradient of the graph of $y=f\left(x\right)$ at $x=2$.

Find an expression for the total length of the ribbon $L$ in terms of $x$ and $y$.

Show that $L=2x+\frac{300}{x}+22$

Find $\frac{dL}{dx}$

Solve $\frac{dL}{dx}=0$

Use differentiation to show that $12a+4b+c=0$.

Find $S\prime \left(x\right)$.

Interpret your answer to (b)(i) in context.