| Date | November 2016 | Marks available | 4 | Reference code | 16N.1.SL.TZ0.T_14 |
| Level | Standard Level | Paper | Paper 1 | Time zone | Time zone 0 |
| Command term | Find | Question number | T_14 | Adapted from | N/A |
Question
The equation of a curve is .
The gradient of the tangent to the curve at a point P is .
Find .
Find the coordinates of P.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
(A1)(A1) (C2)
Note: Award (A1) for , award (A1) for .
Award at most (A1)(A0) if there are any extra terms.
[2 marks]
(M1)
Note: Award (M1) for equating their answer to part (a) to .
(A1)(ft)
Note: Follow through from part (a). Award (M0)(A0) for seen without working.
(M1)
Note: Award (M1) substituting their into the original function.
(A1)(ft) (C4)
Note: Accept .
[4 marks]
Examiners report
Syllabus sections
-
22M.2.SL.TZ2.5a:
Find an expression for in terms of and .
-
18N.2.SL.TZ0.T_6a:
Calculate the area of cloth, in cm2, needed to make Haruka’s bag.
-
18N.2.SL.TZ0.T_6e:
Use your answers to parts (c) and (d) to show that
.
-
18M.2.SL.TZ1.S_1b:
Find f "(x).
-
17M.2.SL.TZ1.T_6d.i:
Find .
-
EXN.1.SL.TZ0.7b:
Show that the normal to the curve at the point where is .
-
17M.2.AHL.TZ1.H_8b:
Calculate when .
-
21M.2.SL.TZ2.5e:
Find the value of which maximizes the volume of the box.
-
22M.1.SL.TZ2.11a:
Find .
-
22M.1.SL.TZ2.11b:
Use your answer to part (a) to find the gradient of .
-
22M.1.SL.TZ1.9a:
Find .
-
21N.1.SL.TZ0.12b.i:
Solve .
-
16N.2.SL.TZ0.T_6b:
Express this volume in .
-
SPM.2.SL.TZ0.4d:
Find .
-
19M.2.SL.TZ1.S_9b:
Find u.
-
18M.2.SL.TZ1.S_1a:
Find f '(x).
-
18M.2.SL.TZ1.S_1c:
Solve f '(x) = f "(x).
-
19M.2.SL.TZ2.T_5f:
Find the equation of the tangent line to the graph of at . Give the equation in the form where, , , and .
-
17N.1.SL.TZ0.T_14b:
Find the point on the graph of at which the gradient of the tangent is equal to 6.
-
18N.2.SL.TZ0.T_6b:
Calculate the volume, in cm3, of the bag.
-
17M.2.SL.TZ2.T_6f:
Write down the number of possible solutions to the equation .
-
18M.2.SL.TZ2.T_6f:
Given that y = 2x3 − 9x2 + 12x + 2 = k has three solutions, find the possible values of k.
-
18M.1.SL.TZ2.S_9c:
Given that there is a minimum value for C, find this minimum value in terms of .
-
19M.2.SL.TZ1.S_9d.iii:
Hence or otherwise, find the obtuse angle formed by the tangent line to at and the tangent line to at .
-
18N.2.SL.TZ0.T_6h:
The cloth used to make Nanako’s bag costs 4 Japanese Yen (JPY) per cm2.
Find the cost of the cloth used to make Nanako’s bag.
-
18M.2.SL.TZ2.T_6a:
Sketch the curve for −1 < x < 3 and −2 < y < 12.
-
17N.2.SL.TZ0.T_5b.ii:
Find .
-
17M.2.AHL.TZ1.H_12e:
Find the inverse function and state its domain.
-
SPM.2.SL.TZ0.4a:
Calculate the surface area of the box in cm2.
-
16N.1.SL.TZ0.S_10b:
(i) Find the first three derivatives of .
(ii) Given that , find .
-
17M.1.SL.TZ2.S_6b:
Find .
-
19N.2.SL.TZ0.T_6c:
Given the design constraint that , show that .
-
17M.2.SL.TZ2.T_6d.i:
Write down the -coordinates of these two points;
-
18M.2.SL.TZ2.T_6b:
A teacher asks her students to make some observations about the curve.
Three students responded.
Nadia said “The x-intercept of the curve is between −1 and zero”.
Rick said “The curve is decreasing when x < 1 ”.
Paula said “The gradient of the curve is less than zero between x = 1 and x = 2 ”.State the name of the student who made an incorrect observation.
-
17M.2.SL.TZ2.T_6a:
Write down the -intercept of the graph.
-
16N.1.SL.TZ0.S_10c:
(i) Find .
(ii) Hence, show that .
-
18M.2.AHL.TZ2.H_11b.i:
Find the coordinates of P and Q.
-
17N.1.SL.TZ0.T_14a:
Write down the derivative of .
-
17M.2.SL.TZ1.T_6d.ii:
Hence justify that is decreasing at .
-
17N.1.AHL.TZ0.H_7:
The folium of Descartes is a curve defined by the equation , shown in the following diagram.
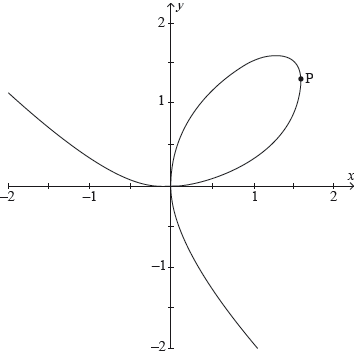
Determine the exact coordinates of the point P on the curve where the tangent line is parallel to the -axis.
-
19M.1.SL.TZ1.T_15c:
Find the value of when the area of the curved surface is maximized.
-
19N.2.SL.TZ0.T_6e:
Using your answer to part (d), show that is a maximum when is equal to .
-
19N.2.SL.TZ0.T_6h:
Use your answer to part (f) to identify the shape of the speaker with the best quality of sound.
-
17M.2.SL.TZ2.T_6c.ii:
Find .
-
19M.2.SL.TZ1.S_9d.i:
Find .
-
18N.2.SL.TZ0.T_6f:
Find .
-
19N.1.SL.TZ0.T_14a:
Write down the value of .
-
18M.1.SL.TZ2.T_14c:
Find the x-coordinate of the point at which the normal to the graph of f has gradient .
-
19N.2.SL.TZ0.T_6g:
Calculate the maximum value of .
-
19M.2.SL.TZ1.S_9c:
Find the acute angle between and .
-
18N.1.SL.TZ0.S_10b.ii:
Hence, find the equation of L in terms of .
-
18N.1.SL.TZ0.S_10a:
Find the coordinates of P.
-
16N.1.AHL.TZ0.H_9a:
Find an expression for in terms of and .
-
18N.2.SL.TZ0.T_6d:
Write down and simplify an expression in x and y for the area of cloth, A, used to make Nanako’s bag.
-
17M.2.AHL.TZ1.H_12c:
Explain why is an even function.
-
17M.2.SL.TZ1.S_6:
Let . Find the term in in the expansion of the derivative, .
-
19M.1.SL.TZ2.T_15a:
Find the value of if no vases are sold.
-
19N.2.SL.TZ0.T_6f:
Find the length of the cylinder for which is a maximum.
-
18N.2.SL.TZ0.T_6g:
Use your answer to part (f) to show that the width of Nanako’s bag is 12 cm.
-
17M.2.SL.TZ2.T_6c.i:
Show that .
-
19N.2.SL.TZ0.T_6d:
Find .
-
18N.1.SL.TZ0.S_10b.i:
Find .
-
18M.1.SL.TZ2.T_14a:
Find f'(x)
-
16N.1.AHL.TZ0.H_9b:
Find the equations of the tangents to this curve at the points where the curve intersects the line .
-
18M.2.AHL.TZ2.H_11c:
Find the coordinates of the three points on C, nearest the origin, where the tangent is parallel to the line .
-
18N.1.SL.TZ0.S_10c:
The graph of has a local minimum at the point Q. The line L passes through Q.
Find the value of .
-
19N.2.SL.TZ0.T_6a:
Write down an expression for , the volume (cm3) of the speaker, in terms of , and .
-
17N.2.SL.TZ0.T_5b.i:
Expand the expression for .
-
19M.2.SL.TZ1.T_6a:
Show that .
-
17M.2.AHL.TZ1.H_12g.ii:
Hence, show that there are no solutions to .
-
17M.2.SL.TZ1.T_6b.ii:
Find the equation of the tangent to the graph of at . Give your answer in the form .
-
19M.1.SL.TZ2.T_15b:
Differentiate .
-
17N.2.SL.TZ0.T_5e:
Write down the coordinates of the point of intersection.
-
18M.2.AHL.TZ2.H_11b.ii:
Given that the gradients of the tangents to C at P and Q are m1 and m2 respectively, show that m1 × m2 = 1.
-
17M.2.SL.TZ2.T_6d.ii:
Write down the intervals where the gradient of the graph of is positive.
-
19N.1.SL.TZ0.T_14c:
At the point where , the gradient of the tangent to the curve is .
Find the value of .
-
16N.2.SL.TZ0.T_6f:
Using your answer to part (e), find the value of which minimizes .
-
18M.2.AHL.TZ2.H_11a:
Show that .
-
18N.2.SL.TZ0.T_6c:
Use this value to write down, and simplify, the equation in x and y for the volume of Nanako’s bag.
-
20N.1.SL.TZ0.S_10a.ii:
Show that the equation of is .
-
20N.1.SL.TZ0.T_13b:
Write down the gradient of this tangent.
-
17M.2.SL.TZ2.T_6g:
The equation , where , has four solutions. Find the possible values of .
-
17M.2.AHL.TZ1.H_12f:
Find .
-
16N.2.SL.TZ0.T_6e:
Find .
-
17N.2.SL.TZ0.T_5c:
Use your answer to part (b)(ii) to find the values of for which is increasing.
-
18M.1.SL.TZ2.S_9b:
Show that .
-
18M.2.SL.TZ2.T_6d:
Find .
-
17N.2.SL.TZ0.T_5a:
Find the exact value of each of the zeros of .
-
17M.2.SL.TZ2.T_6b:
Find .
-
SPM.2.SL.TZ0.4e:
Find the least number of boxes which must be sold each week in order to make a profit.
-
17M.2.AHL.TZ1.H_2a:
Find in terms of and .
-
17M.2.AHL.TZ1.H_12d:
Explain why the inverse function does not exist.
-
17M.2.AHL.TZ1.H_12g.i:
Hence, show that there are no solutions to ;
-
17M.2.SL.TZ1.T_6b.i:
Show that .
-
17M.2.SL.TZ1.T_6a:
Find .
-
19M.2.SL.TZ2.T_5d:
Find .
-
17M.2.SL.TZ2.T_6e:
Write down the range of .
-
20N.1.SL.TZ0.S_10a.i:
Find in terms of and .
-
20N.1.SL.TZ0.T_13c:
Find the value of .
-
19M.2.SL.TZ1.T_6b:
Find the coordinates of the local minimum.
-
SPM.2.SL.TZ0.4b:
Calculate the length AG.
-
17M.2.AHL.TZ1.H_8a:
Find an expression for the volume of water in the trough in terms of .
-
19N.1.SL.TZ0.T_14b:
Find .
-
18M.1.SL.TZ2.T_14b:
Find the gradient of the graph of f at .
-
17M.2.SL.TZ1.T_6e:
Find the -coordinate of the local minimum.
-
16N.2.SL.TZ0.T_6c:
Write down, in terms of and , an equation for the volume of this water container.
-
17M.2.AHL.TZ1.H_2b:
Determine the equation of the tangent to at the point
-
17N.2.SL.TZ0.T_5d:
Draw the graph of for and . Use a scale of 2 cm to represent 1 unit on the -axis and 1 cm to represent 5 units on the -axis.
-
16N.2.SL.TZ0.T_6a:
Write down a formula for , the surface area to be coated.
-
16N.2.SL.TZ0.T_6h:
Find the least number of cans of water-resistant material that will coat the area in part (g).
-
19M.2.SL.TZ1.T_6d:
Determine the equation of the normal at in the form .
-
19M.2.SL.TZ1.S_9a:
Find the gradient of .
-
19M.2.SL.TZ1.S_9d.ii:
Hence, write down .
-
17M.2.SL.TZ1.T_6c:
Use your answer to part (a) and the value of , to find the -coordinates of the stationary points of the graph of .
-
21M.2.AHL.TZ1.2a.i:
Find .
-
16N.2.SL.TZ0.T_6d:
Show that .
-
SPM.2.SL.TZ0.4c:
Find the number of boxes that should be sold each week to maximize the profit.
-
17M.2.AHL.TZ1.H_12b:
Sketch the graph of showing clearly the equations of asymptotes and the coordinates of any intercepts with the axes.
-
19N.2.SL.TZ0.T_6b:
Write down an equation for the surface area of the speaker in terms of , and .
-
20N.1.SL.TZ0.S_10c:
The graph of is translated by to give the graph of .
In the following diagram:- point lies on the graph of
- points , and lie on the vertical asymptote of
- points and lie on the horizontal asymptote of
- point lies on the -axis such that is parallel to .
Line is the tangent to the graph of at , and passes through and .
Given that triangle and rectangle have equal areas, find the gradient of in terms of .
-
19M.2.SL.TZ1.T_6c:
Write down the interval where the gradient of the graph of is negative.
-
20N.1.SL.TZ0.T_13a:
Write down .
-
20N.1.SL.TZ0.S_10b:
Find the area of triangle in terms of .
-
21M.2.SL.TZ2.5d:
Find an expression for .
-
19M.1.SL.TZ1.T_15a:
Write down an equation for the area, , of the curved surface in terms of .
-
17M.2.AHL.TZ1.H_12a:
Find the largest possible domain for to be a function.
-
16N.2.SL.TZ0.T_6g:
Find the value of this minimum area.
-
16N.1.SL.TZ0.T_14a:
Find .
-
18M.1.SL.TZ2.S_9a:
Express h in terms of r.
-
17M.1.SL.TZ2.S_6a:
Find .
-
EXN.1.SL.TZ0.7a:
Find an expression for .
-
18M.1.AHL.TZ1.H_2b:
Hence find the values of θ for which .
-
18M.1.AHL.TZ1.H_2a:
Find
-
19M.1.AHL.TZ1.H_7:
Find the coordinates of the points on the curve at which .
-
19M.1.SL.TZ1.T_15b:
Find .
-
18M.1.SL.TZ1.S_7:
Consider f(x), g(x) and h(x), for x∈ where h(x) = (x).
Given that g(3) = 7 , g′ (3) = 4 and f ′ (7) = −5 , find the gradient of the normal to the curve of h at x = 3.
-
16N.1.SL.TZ0.S_10a:
(i) Find the first four derivatives of .
(ii) Find .
-
EXN.2.SL.TZ0.2e:
Hence or otherwise find the minimum length of ribbon required.
-
19M.2.SL.TZ2.T_5e:
Find the gradient of the graph of at .
-
EXN.2.SL.TZ0.2a:
Find an expression for the total length of the ribbon in terms of and .
-
EXN.2.SL.TZ0.2b:
Show that
-
EXN.2.SL.TZ0.2c:
Find
-
EXN.2.SL.TZ0.2d:
Solve
-
EXN.2.SL.TZ0.6d:
Use differentiation to show that .
-
21N.1.SL.TZ0.12a:
Find .
-
21N.1.SL.TZ0.12b.ii:
Interpret your answer to (b)(i) in context.

