| Date | November 2015 | Marks available | 2 | Reference code | 15N.2.sl.TZ0.1 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 1 | Adapted from | N/A |
Question
The following diagram shows a circle with centre \(O\) and radius \(3\) cm.
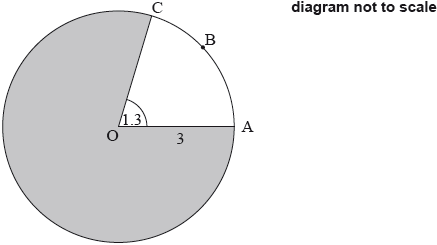
Points A, B, and C lie on the circle, and \({\rm{A\hat OC}} = 1.3{\text{ radians}}\).
Find the length of arc \(ABC\).
Find the area of the shaded region.
Markscheme
correct substitution (A1)
eg\(\;\;\;l = 1.3 \times 3\)
\(l\) = \(3.9\) (cm) A1 N2
[2 marks]
METHOD 1
valid approach (M1)
eg\(\;\;\;\)finding reflex angle, \(2\pi - {\rm{C\hat OA}}\)
correct angle (A1)
eg\(\;\;\;2\pi - 1.3,{\text{ }}4.98318\)
correct substitution (A1)
eg\(\;\;\;\frac{1}{2}(2\pi - 1.3){3^2}\)
\(22.4243\)
\({\text{area}} = 9\pi - 5.85{\text{ (exact), }}22.4{\text{ }} {\text{ }}({\text{c}}{{\text{m}}^2})\) A1 N3
METHOD 2
correct area of small sector (A1)
eg\(\;\;\;\frac{1}{2}(1.3){3^2},{\text{ }}5.85\)
valid approach (M1)
eg\(\;\;\;\)circle − small sector, \(\pi {r^2} - \frac{1}{2}\theta {r^2}\)
correct substitution (A1)
eg\(\;\;\;\pi ({3^2}) - \frac{1}{2}(1.3){3^2}\)
\(22.4243\)
\({\text{area}} = 9\pi - 5.85{\text{ }}({\text{exact}}),{\text{ }}22.4{\text{ }}{\text{ }}({\text{c}}{{\text{m}}^2})\) A1 N3
[4 marks]
Total [6 marks]

