| Date | November 2016 | Marks available | 1 | Reference code | 16N.2.sl.TZ0.3 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Write down | Question number | 3 | Adapted from | N/A |
Question
The following diagram shows a circle, centre O and radius \(r\) mm. The circle is divided into five equal sectors.
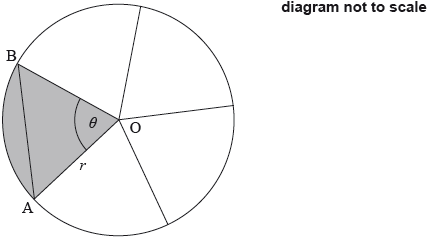
One sector is OAB, and \({\rm{A\hat OB}} = \theta \).
The area of sector AOB is \(20\pi {\text{ m}}{{\text{m}}^2}\).
Write down the exact value of \(\theta \) in radians.
Find the value of \(r\).
Find AB.
Markscheme
\(\theta = \frac{{2\pi }}{5}\) A1 N1
[1 mark]
correct expression for area (A1)
eg\(\,\,\,\,\,\)\(A = \frac{1}{2}{r^2}\left( {\frac{{2\pi }}{5}} \right),{\text{ }}\frac{{\pi {r^2}}}{5}\)
evidence of equating their expression to \(20\pi \) (M1)
eg\(\,\,\,\,\,\)\(\frac{1}{2}{r^2}\left( {\frac{{2\pi }}{5}} \right) = 20\pi ,{\text{ }}{r^2} = 100,{\text{ }}r = \pm 10\)
\(r = 10\) A1 N2
[3 marks]
METHOD 1
evidence of choosing cosine rule (M1)
eg\(\,\,\,\,\,\)\({a^2} = {b^2} + {c^2} - 2bc\cos A\)
correct substitution of their \(r\) and \(\theta \) into RHS (A1)
eg\(\,\,\,\,\,\)\({10^2} + {10^2} - 2 \times 10 \times 1{\text{0}}\cos \left( {\frac{{2\pi }}{5}} \right)\)
11.7557
\({\text{AB}} = 11.8{\text{ (mm)}}\) A1 N2
METHOD 2
evidence of choosing sine rule (M1)
eg\(\,\,\,\,\,\)\(\frac{{\sin A}}{a} = \frac{{\sin B}}{b}\)
correct substitution of their \(r\) and \(\theta \) (A1)
eg\(\,\,\,\,\,\)\(\frac{{\sin \frac{{2\pi }}{5}}}{{{\text{AB}}}} = \frac{{\sin \left( {\frac{1}{2}\left( {\pi - \frac{{2\pi }}{5}} \right)} \right)}}{{10}}\)
11.7557
\({\text{AB}} = 11.8{\text{ (mm)}}\) A1 N2
[3 marks]

