| Date | November 2010 | Marks available | 4 | Reference code | 10N.1.sl.TZ0.3 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 3 | Adapted from | N/A |
Question
The diagram shows two concentric circles with centre O.
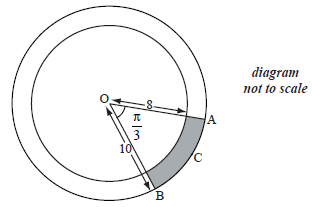
The radius of the smaller circle is 8 cm and the radius of the larger circle is 10 cm.
Points A, B and C are on the circumference of the larger circle such that \({\rm{A}}\widehat {\rm{O}}{\rm{B}}\) is \(\frac{\pi }{3}\) radians.
Find the length of the arc ACB .
Find the area of the shaded region.
Markscheme
correct substitution in \(l = r\theta \) (A1)
e.g. \(10 \times \frac{\pi }{3}\) , \(\frac{1}{6} \times 2\pi \times 10\)
arc length \( = \frac{{20\pi }}{6}\) \(\left( { = \frac{{10\pi }}{3}} \right)\) A1 N2
[2 marks]
area of large sector \( = \frac{1}{2} \times {10^2} \times \frac{\pi }{3}\) \(\left( { = \frac{{100\pi }}{6}} \right)\) (A1)
area of small sector \( = \frac{1}{2} \times {8^2} \times \frac{\pi }{3}\) \(\left( { = \frac{{64\pi }}{6}} \right)\) (A1)
evidence of valid approach (seen anywhere) M1
e.g. subtracting areas of two sectors, \(\frac{1}{2} \times \frac{\pi }{3}({10^2} - {8^2})\)
area shaded \( = 6\pi \) (accept \(\frac{{36\pi }}{6}\) , etc.) A1 N3
[4 marks]
Examiners report
This question was very well done by the majority of candidates. Some candidates correctly substituted the values into the formulas, but failed to do the calculations and write their answers in finished form.
Nearly all used the correct method of subtracting the sector areas in part (b), though multiplying with fractions proved challenging for some candidates.

