| Date | May 2015 | Marks available | 2 | Reference code | 15M.1.sl.TZ1.2 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 2 | Adapted from | N/A |
Question
The following diagram shows a circle with centre \(O\) and a radius of \(10\) cm. Points \(A\), \(B\) and \(C\) lie on the circle.
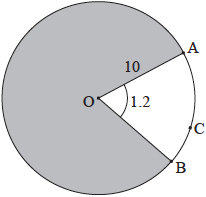
Angle \(AOB\) is \(1.2\) radians.
Find the length of \({\text{arc ACB}}\).
Find the perimeter of the shaded region.
Markscheme
correct substitution (A1)
eg\(\;\;\;10(1.2)\)
\(ACB\) is \(12{\text{ (cm)}}\) A1 N2
[2 marks]
valid approach to find major arc (M1)
eg\(\;\;\;\)circumference \( - {\text{AB}}\), major angle \({\text{AOB}} \times {\text{radius}}\)
correct working for arc length (A1)
eg\(\;\;\;2\pi (10) - 12,{\text{ }}10(2 \times 3.142 - 1.2),{\text{ }}2\pi (10) - 12 + 20\)
perimeter is \(20\pi + 8\;\;\;( = 70.8){\text{ (cm)}}\) A1 N2
[3 marks]
Total [5 marks]
Examiners report
Most candidates were able to find the minor arc length. Similarly most candidates successfully found the major arc length in part b) but did not go on to add the two radii. Quite a few candidates worked with decimal approximations, rather than in terms of \(\pi \).
Most candidates were able to find the minor arc length. Similarly most candidates successfully found the major arc length in part b) but did not go on to add the two radii. Quite a few candidates worked with decimal approximations, rather than in terms of \(\pi \).

