| Date | November 2011 | Marks available | 2 | Reference code | 11N.2.sl.TZ0.3 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 3 | Adapted from | N/A |
Question
Consider the following circle with centre O and radius 6.8 cm.
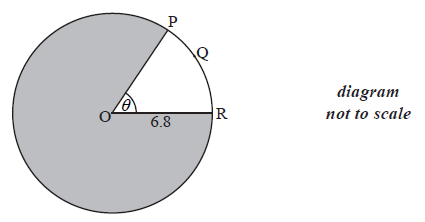
The length of the arc PQR is 8.5 cm.
Find the value of \(\theta \) .
Find the area of the shaded region.
Markscheme
correct substitution (A1)
e.g. \(8.5 = \theta (6.8)\) , \(\theta = \frac{{8.5}}{{6.8}}\)
\(\theta = 1.25\) (accept \({71.6^ \circ }\) ) A1 N2
[2 marks]
METHOD 1
correct substitution into area formula (seen anywhere) (A1)
e.g. \(A = \pi {(6.8)^2}\) , \(145.267 \ldots \)
correct substitution into area formula (seen anywhere) (A1)
e.g. \(A = \frac{1}{2}(1.25)({6.8^2})\) , 28.9
valid approach M1
e.g. \(\pi {(6.8)^2} - \frac{1}{2}(1.25)({6.8^2})\) ; \(145.267 \ldots - 28.9\) ; \(\pi {r^2} - \frac{1}{2}{r^2}\sin \theta \)
\(A = 116\) (\({\text{c}}{{\text{m}}^2}\)) A1 N2
METHOD 2
attempt to find reflex angle (M1)
e.g. \(2\pi - \theta \) , \(360 - 1.25\)
correct reflex angle (A1)
\({\rm{A}}\widehat {\rm{O}}{\rm{B}} = 2\pi - 1.25\) (\( = 5.03318 \ldots \))
correct substitution into area formula A1
e.g. \(A = \frac{1}{2}(5.03318 \ldots )({6.8^2})\)
\(A = 116\) (\({\text{c}}{{\text{m}}^2}\)) A1 N2
[4 marks]
Examiners report
Part (a) was almost universally done correctly.
Many also had little trouble in part (b), with most subtracting from the circle's area, and a minority using the reflex angle. A few candidates worked in degrees, although some of these did so incorrectly by using the radian area formula. Some candidates only found the area of the unshaded sector.

