| Date | May 2008 | Marks available | 3 | Reference code | 08M.2.sl.TZ1.4 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Solve | Question number | 4 | Adapted from | N/A |
Question
Let \(f(x) = 4{\tan ^2}x - 4\sin x\) , \( - \frac{\pi }{3} \le x \le \frac{\pi }{3}\) .
On the grid below, sketch the graph of \(y = f(x)\) .
Solve the equation \(f(x) = 1\) .
Markscheme
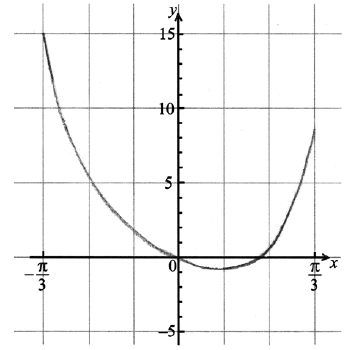A1A1A1 N3
Note: Award A1 for passing through \((0{\text{, }}0)\), A1 for correct shape, A1 for a range of approximately \( - 1\) to 15.
[3 marks]
evidence of attempt to solve \(f(x) = 1\) (M1)
e.g. line on sketch, using \(\tan x = \frac{{\sin x}}{{\cos x}}\)
\(x = - 0.207\) , \(x = 0.772\) A1A1 N3
[3 marks]
Examiners report
In part (a), some did not realize that they should copy the curve from their GDC, paying attention to domain and range.
Not using their GDC, and trying to solve the equation analytically in part (b) proved to be very difficult for many. A common error was to substitute \(x = 1\) .
