| Date | May 2017 | Marks available | 1 | Reference code | 17M.2.sl.TZ1.10 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Write down | Question number | 10 | Adapted from | N/A |
Question
Let \(f(x) = \ln x\) and \(g(x) = 3 + \ln \left( {\frac{x}{2}} \right)\), for \(x > 0\).
The graph of \(g\) can be obtained from the graph of \(f\) by two transformations:
\[\begin{array}{*{20}{l}} {{\text{a horizontal stretch of scale factor }}q{\text{ followed by}}} \\ {{\text{a translation of }}\left( {\begin{array}{*{20}{c}} h \\ k \end{array}} \right).} \end{array}\]
Let \(h(x) = g(x) \times \cos (0.1x)\), for \(0 < x < 4\). The following diagram shows the graph of \(h\) and the line \(y = x\).
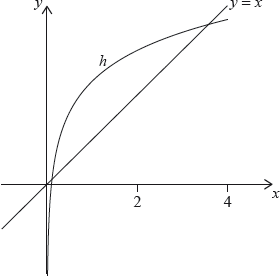
The graph of \(h\) intersects the graph of \({h^{ - 1}}\) at two points. These points have \(x\) coordinates 0.111 and 3.31 correct to three significant figures.
Write down the value of \(q\);
Write down the value of \(h\);
Write down the value of \(k\).
Find \(\int_{0.111}^{3.31} {\left( {h(x) - x} \right){\text{d}}x} \).
Hence, find the area of the region enclosed by the graphs of \(h\) and \({h^{ - 1}}\).
Let \(d\) be the vertical distance from a point on the graph of \(h\) to the line \(y = x\). There is a point \({\text{P}}(a,{\text{ }}b)\) on the graph of \(h\) where \(d\) is a maximum.
Find the coordinates of P, where \(0.111 < a < 3.31\).
Markscheme
\(q = 2\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 - \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) - \ln (2)\).
[1 mark]
\(h = 0\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 - \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) - \ln (2)\).
[1 mark]
\(k = 3\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 - \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) - \ln (2)\).
[1 mark]
2.72409
2.72 A2 N2
[2 marks]
recognizing area between \(y = x\) and \(h\) equals 2.72 (M1)
eg\(\,\,\,\,\,\)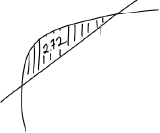
recognizing graphs of \(h\) and \({h^{ - 1}}\) are reflections of each other in \(y = x\) (M1)
eg\(\,\,\,\,\,\)area between \(y = x\) and \(h\) equals between \(y = x\) and \({h^{ - 1}}\)
\(2 \times 2.72\int_{0.111}^{3.31} {\left( {x - {h^{ - 1}}(x)} \right){\text{d}}x = 2.72} \)
5.44819
5.45 A1 N3
[??? marks]
valid attempt to find \(d\) (M1)
eg\(\,\,\,\,\,\)difference in \(y\)-coordinates, \(d = h(x) - x\)
correct expression for \(d\) (A1)
eg\(\,\,\,\,\,\)\(\left( {\ln \frac{1}{2}x + 3} \right)(\cos 0.1x) - x\)
valid approach to find when \(d\) is a maximum (M1)
eg\(\,\,\,\,\,\)max on sketch of \(d\), attempt to solve \(d’ = 0\)
0.973679
\(x = 0.974\) A2 N4
substituting their \(x\) value into \(h(x)\) (M1)
2.26938
\(y = 2.27\) A1 N2
[7 marks]

