| Date | May 2017 | Marks available | 3 | Reference code | 17M.2.sl.TZ2.6 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 6 | Adapted from | N/A |
Question
Let \(f(x) = {x^2} - 1\) and \(g(x) = {x^2} - 2\), for \(x \in \mathbb{R}\).
Show that \((f \circ g)(x) = {x^4} - 4{x^2} + 3\).
On the following grid, sketch the graph of \((f \circ g)(x)\), for \(0 \leqslant x \leqslant 2.25\).
The equation \((f \circ g)(x) = k\) has exactly two solutions, for \(0 \leqslant x \leqslant 2.25\). Find the possible values of \(k\).
Markscheme
attempt to form composite in either order (M1)
eg\(\,\,\,\,\,\)\(f({x^2} - 2),{\text{ }}{({x^2} - 1)^2} - 2\)
\(({x^4} - 4{x^2} + 4) - 1\) A1
\((f \circ g)(x) = {x^4} - 4{x^2} + 3\) AG N0
[2 marks]
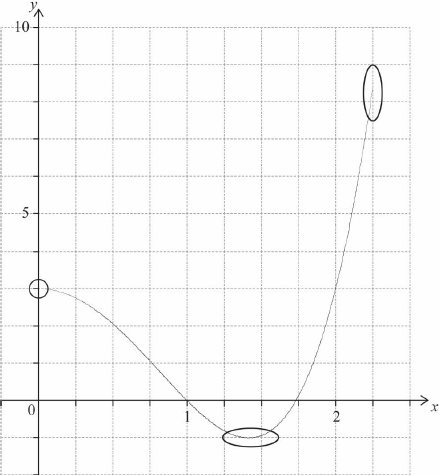 A1
A1
A1A1 N3
Note: Award A1 for approximately correct shape which changes from concave down to concave up. Only if this A1 is awarded, award the following:
A1 for left hand endpoint in circle and right hand endpoint in oval,
A1 for minimum in oval.
[3 marks]
evidence of identifying max/min as relevant points (M1)
eg\(\,\,\,\,\,\)\(x = 0,{\text{ }}1.41421,{\text{ }}y = - 1,{\text{ }}3\)
correct interval (inclusion/exclusion of endpoints must be correct) A2 N3
eg\(\,\,\,\,\,\)\( - 1 < k \leqslant 3,{\text{ }}\left] { - 1,{\text{ 3}}} \right],{\text{ }}( - 1,{\text{ }}3]\)
[3 marks]

