| Date | November 2017 | Marks available | 3 | Reference code | 17N.1.sl.TZ0.8 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 8 | Adapted from | N/A |
Question
Let \(f(x) = {x^2} - x\), for \(x \in \mathbb{R}\). The following diagram shows part of the graph of \(f\).
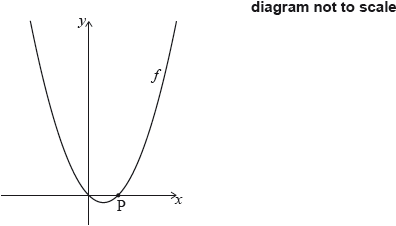
The graph of \(f\) crosses the \(x\)-axis at the origin and at the point \({\text{P}}(1,{\text{ }}0)\).
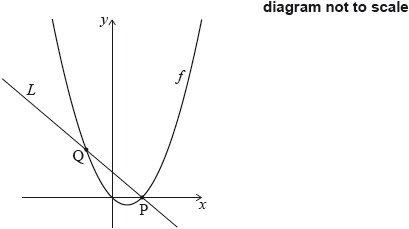
The line L is the normal to the graph of f at P.
The line \(L\) intersects the graph of \(f\) at another point Q, as shown in the following diagram.
Show that \(f’(1) = 1\).
Find the equation of \(L\) in the form \(y = ax + b\).
Find the \(x\)-coordinate of Q.
Find the area of the region enclosed by the graph of \(f\) and the line \(L\).
Markscheme
\(f’(x) = 2x - 1\) A1A1
correct substitution A1
eg\(\,\,\,\,\,\)\(2(1) - 1,{\text{ }}2 - 1\)
\(f’(1) = 1\) AG N0
[3 marks]
correct approach to find the gradient of the normal (A1)
eg\(\,\,\,\,\,\)\(\frac{{ - 1}}{{f'(1)}},{\text{ }}{m_1}{m_2} = - 1,{\text{ slope}} = - 1\)
attempt to substitute correct normal gradient and coordinates into equation of a line (M1)
eg\(\,\,\,\,\,\)\(y - 0 = - 1(x - 1),{\text{ }}0 = - 1 + b,{\text{ }}b = 1,{\text{ }}L = - x + 1\)
\(y = - x + 1\) A1 N2
[3 marks]
equating expressions (M1)
eg\(\,\,\,\,\,\)\(f(x) = L,{\text{ }} - x + 1 = {x^2} - x\)
correct working (must involve combining terms) (A1)
eg\(\,\,\,\,\,\)\({x^2} - 1 = 0,{\text{ }}{x^2} = 1,{\text{ }}x = 1\)
\(x = - 1\,\,\,\,\,\left( {{\text{accept }}Q( - 1,{\text{ }}2)} \right)\) A2 N3
[4 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\(\int {L - f,{\text{ }}\int_{ - 1}^1 {(1 - {x^2}){\text{d}}x} } \), splitting area into triangles and integrals
correct integration (A1)(A1)
eg\(\,\,\,\,\,\)\(\left[ {x - \frac{{{x^3}}}{3}} \right]_{ - 1}^1,{\text{ }} - \frac{{{x^3}}}{3} - \frac{{{x^2}}}{2} + \frac{{{x^2}}}{2} + x\)
substituting their limits into their integrated function and subtracting (in any order) (M1)
eg\(\,\,\,\,\,\)\(1 - \frac{1}{3} - \left( { - 1 - \frac{{ - 1}}{3}} \right)\)
Note: Award M0 for substituting into original or differentiated function.
area \( = \frac{4}{3}\) A2 N3
[6 marks]

