| Date | May 2016 | Marks available | [N/A] | Reference code | 16M.2.sl.TZ1.10 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Question number | 10 | Adapted from | N/A |
Question
The points A and B lie on a line \(L\), and have position vectors \(\left( {\begin{array}{*{20}{c}} { - 3} \\ { - 2} \\ 2 \end{array}} \right)\) and \(\left( {\begin{array}{*{20}{c}} 6 \\ 4 \\ { - 1} \end{array}} \right)\) respectively. Let O be the origin. This is shown on the following diagram.
The point C also lies on \(L\), such that \(\overrightarrow {{\text{AC}}} = 2\overrightarrow {{\text{CB}}} \).
Let \(\theta \) be the angle between \(\overrightarrow {{\text{AB}}} \) and \(\overrightarrow {{\text{OC}}} \).
Let D be a point such that \(\overrightarrow {{\text{OD}}} = k\overrightarrow {{\text{OC}}} \), where \(k > 1\). Let E be a point on \(L\) such that \({\rm{C\hat ED}}\) is a right angle. This is shown on the following diagram.
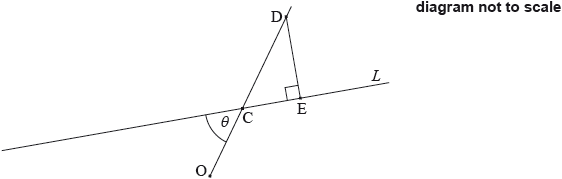
Find \(\overrightarrow {{\text{AB}}} \).
Show that \(\overrightarrow {{\text{OC}}} = \left( {\begin{array}{*{20}{c}} 3 \\ 2 \\ 0 \end{array}} \right)\).
Find \(\theta \).
(i) Show that \(\left| {\overrightarrow {{\text{DE}}} } \right| = (k - 1)\left| {\overrightarrow {{\text{OC}}} } \right|\sin \theta \).
(ii) The distance from D to line \(L\) is less than 3 units. Find the possible values of \(k\).
Markscheme
valid approach (addition or subtraction) (M1)
eg\(\,\,\,\,\,\)\({\text{AO}} + {\text{OB}},{\text{ B}} - {\text{A}}\)
\(\overrightarrow {{\text{AB}}} = \left( {\begin{array}{*{20}{c}} 9 \\ 6 \\ { - 3} \end{array}} \right)\) A1 N2
[2 marks]
METHOD 1
valid approach using \(\overrightarrow {{\text{OC}}} = \left( {\begin{array}{*{20}{c}} x \\ y \\ z \end{array}} \right)\) (M1)
eg\(\,\,\,\,\,\)\(\overrightarrow {{\text{AC}}} = \left( {\begin{array}{*{20}{c}} {x + 3} \\ {y + 2} \\ {z - 2} \end{array}} \right),{\text{ }}\overrightarrow {{\text{CB}}} = \left( {\begin{array}{*{20}{c}} {6 - x} \\ {4 - y} \\ { - 1 - z} \end{array}} \right)\)
correct working A1
eg\(\,\,\,\,\,\)\(\left( {\begin{array}{*{20}{c}} {x + 3} \\ {y + 2} \\ {z - 2} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {12 - 2x} \\ {8 - 2y} \\ { - 2 - 2z} \end{array}} \right)\)
all three equations A1
eg\(\,\,\,\,\,\)\(x + 3 = 12 - 2x,{\text{ }}y + 2 = 8 - 2y,{\text{ }}z - 2 = - 2 - 2z\),
\(\overrightarrow {{\text{OC}}} = \left( {\begin{array}{*{20}{c}} 3 \\ 2 \\ 0 \end{array}} \right)\) AG N0
METHOD 2
valid approach (M1)
eg\(\,\,\,\,\,\)\(\overrightarrow {{\text{OC}}} - \overrightarrow {{\text{OA}}} = 2\left( {\overrightarrow {{\text{OB}}} - \overrightarrow {{\text{OC}}} } \right)\)
correct working A1
eg\(\,\,\,\,\,\)\(3\overrightarrow {{\text{OC}}} = 2\overrightarrow {{\text{OB}}} + \overrightarrow {{\text{OA}}} \)
correct substitution of \(\overrightarrow {{\text{OB}}} \) and \(\overrightarrow {{\text{OA}}} \) A1
eg\(\,\,\,\,\,\)\(3\overrightarrow {{\text{OC}}} = 2\left( {\begin{array}{*{20}{c}} 6 \\ 4 \\ { - 1} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} { - 3} \\ { - 2} \\ 2 \end{array}} \right),{\text{ }}3\overrightarrow {{\text{OC}}} = \left( {\begin{array}{*{20}{c}} 9 \\ 6 \\ 0 \end{array}} \right)\)
\(\overrightarrow {{\text{OC}}} = \left( {\begin{array}{*{20}{c}} 3 \\ 2 \\ 0 \end{array}} \right)\) AG N0
METHOD 3
valid approach (M1)
eg\(\,\,\,\,\,\)\(\overrightarrow {{\text{AC}}} = \frac{2}{3}\overrightarrow {{\text{AB}}} \), diagram, \(\overrightarrow {{\text{CB}}} = \frac{1}{3}\overrightarrow {{\text{AB}}} \)

correct working A1
eg\(\,\,\,\,\,\)\(\overrightarrow {{\text{AC}}} = \left( {\begin{array}{*{20}{c}} 6 \\ 4 \\ { - 2} \end{array}} \right),{\text{ }}\overrightarrow {{\text{CB}}} = \left( {\begin{array}{*{20}{c}} 3 \\ 2 \\ { - 1} \end{array}} \right)\)
correct working involving \(\overrightarrow {{\text{OC}}} \) A1
eg\(\,\,\,\,\,\)\(\overrightarrow {{\text{OC}}} = \left( {\begin{array}{*{20}{c}} { - 3} \\ { - 2} \\ 2 \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 6 \\ 4 \\ { - 2} \end{array}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} 6 \\ 4 \\ { - 1} \end{array}} \right) - \left( {\begin{array}{*{20}{c}} 3 \\ 2 \\ { - 1} \end{array}} \right)\)
\(\overrightarrow {{\text{OC}}} = \left( {\begin{array}{*{20}{c}} 3 \\ 2 \\ 0 \end{array}} \right)\) AG N0
[3 marks]
finding scalar product and magnitudes (A1)(A1)(A1)
scalar product \( = (9 \times 3) + (6 \times 2) + ( - 3 \times 0){\text{ }}( = 39)\)
magnitudes \(\sqrt {81 + 36 + 9} {\text{ }}( = 11.22),{\text{ }}\sqrt {9 + 4} {\text{ }}( = 3.605)\)
substitution into formula M1
eg\(\,\,\,\,\,\)\(\cos \theta = \frac{{(9 \times 3) + 12}}{{\sqrt {126} \times \sqrt {13} }}\)
\(\theta = 0.270549{\text{ }}({\text{accept }}15.50135^\circ )\)
\(\theta = 0.271{\text{ }}({\text{accept }}15.5^\circ )\) A1 N4
[5 marks]
(i) attempt to use a trig ratio M1
eg\(\,\,\,\,\,\)\(\sin \theta = \frac{{{\text{DE}}}}{{{\text{CD}}}},{\text{ }}\left| {\overrightarrow {{\text{CE}}} } \right| = \left| {\overrightarrow {{\text{CD}}} } \right|\cos \theta \)
attempt to express \(\overrightarrow {{\text{CD}}} \) in terms of \(\overrightarrow {{\text{OC}}} \) M1
eg\(\,\,\,\,\,\)\(\overrightarrow {{\text{OC}}} + \overrightarrow {{\text{CD}}} = \overrightarrow {{\text{OD}}} ,{\text{ OC}} + {\text{CD}} = {\text{OD}}\)
correct working A1
eg\(\,\,\,\,\,\)\(\left| {k\overrightarrow {{\text{OC}}} - \overrightarrow {{\text{OC}}} } \right|\sin \theta \)
\(\left| {\overrightarrow {{\text{DE}}} } \right| = (k - 1)\left| {\overrightarrow {{\text{OC}}} } \right|\sin \theta \) AG N0
(ii) valid approach involving the segment DE (M1)
eg\(\,\,\,\,\,\)recognizing \(\left| {\overrightarrow {{\text{DE}}} } \right| < 3,{\text{ DE}} = 3\)
correct working (accept equation) (A1)
eg\(\,\,\,\,\,\)\((k - 1)(\sqrt {13} )\sin 0.271 < 3,{\text{ }}k - 1 = 3.11324\)
\(1 < k < 4.11{\text{ }}({\text{accept }}k < 4.11{\text{ but not }}k = 4.11)\) A1 N2
[6 marks]
Examiners report
The majority of candidates had little difficulty with parts (a) and (c). The most common error in both these parts were unforced arithmetic errors and occasional misreads of the vectors.
In part (b), candidates who were successful used a variety of different approaches, and it was pleasing to see the vast majority of these being well reasoned, however, there were numerous unsuccessful responses including those who attempted to use the given vector to work backwards. A lack of appropriate vector notation often meant that ideas were not always clearly communicated.
The majority of candidates had little difficulty with parts (a) and (c). The most common error in both these parts were unforced arithmetic errors and occasional misreads of the vectors.
The majority of candidates struggled to make any progress in (d), with very few realizing that simple right-angled trigonometry could be used. Few were able to successfully express CD in terms of OC which was required to show the given result. Very few candidates attempted (d)(ii), with many unable to make the connection with results found in previous parts of the question.

