| Date | May 2017 | Marks available | 6 | Reference code | 17M.1.sl.TZ1.3 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 3 | Adapted from | N/A |
Question
The following diagram shows triangle PQR.
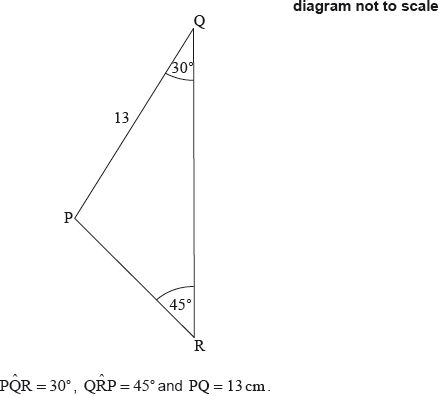
Find PR.
Markscheme
METHOD 1
evidence of choosing the sine rule (M1)
eg\(\,\,\,\,\,\)\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}}\)
correct substitution A1
eg\(\,\,\,\,\,\)\(\frac{x}{{\sin 30}} = \frac{{13}}{{\sin 45}},{\text{ }}\frac{{13\sin 30}}{{\sin 45}}\)
\(\sin 30 = \frac{1}{2},{\text{ }}\sin 45 = \frac{1}{{\sqrt 2 }}\) (A1)(A1)
correct working A1
eg\(\,\,\,\,\,\)\(\frac{1}{2} \times \frac{{13}}{{\frac{1}{{\sqrt 2 }}}},{\text{ }}\frac{1}{2} \times 13 \times \frac{2}{{\sqrt 2 }},{\text{ }}13 \times \frac{1}{2} \times \sqrt 2 \)
correct answer A1 N3
eg\(\,\,\,\,\,\)\({\text{PR}} = \frac{{13\sqrt 2 }}{2},{\text{ }}\frac{{13}}{{\sqrt 2 }}{\text{ (cm)}}\)
METHOD 2 (using height of ΔPQR)
valid approach to find height of ΔPQR (M1)
eg\(\,\,\,\,\,\)\(\sin 30 = \frac{x}{{13}},{\text{ }}\cos 60 = \frac{x}{{13}}\)
\(\sin 30 = \frac{1}{2}{\text{ or }}\cos 60 = \frac{1}{2}\) (A1)
\({\text{height}} = 6.5\) A1
correct working A1
eg\(\,\,\,\,\,\)\(\sin 45 = \frac{{6.5}}{{{\text{PR}}}},{\text{ }}\sqrt {{{6.5}^2} + {{6.5}^2}} \)
correct working (A1)
eg\(\,\,\,\,\,\)\(\sin 45 = \frac{1}{{\sqrt 2 }},{\text{ }}\cos 45 = \frac{1}{{\sqrt 2 }},{\text{ }}\sqrt {\frac{{169 \times 2}}{4}} \)
correct answer A1 N3
eg\(\,\,\,\,\,\)\({\text{PR}} = \frac{{13\sqrt 2 }}{2},{\text{ }}\frac{{13}}{{\sqrt 2 }}{\text{ (cm)}}\)
[6 marks]

