| Date | November 2009 | Marks available | 3 | Reference code | 09N.2.sl.TZ0.8 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 8 | Adapted from | N/A |
Question
The following diagram shows a circle with centre O and radius 4 cm.
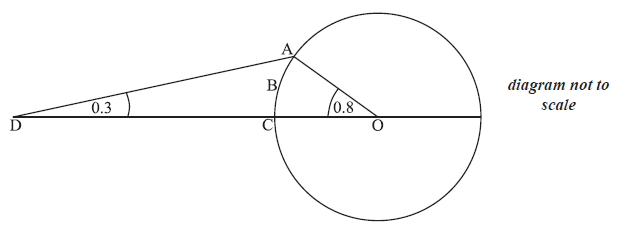
The points A, B and C lie on the circle. The point D is outside the circle, on (OC).
Angle ADC = 0.3 radians and angle AOC = 0.8 radians.
Find AD.
Find OD.
Find the area of sector OABC.
Find the area of region ABCD.
Markscheme
choosing sine rule (M1)
correct substitution A1
e.g. \(\frac{{{\rm{AD}}}}{{\sin 0.8}} = \frac{4}{{\sin 0.3}}\)
\({\text{AD}} = 9.71{\text{ (cm)}}\) A1 N2
[3 marks]
METHOD 1
finding angle \({\rm{OAD}} = \pi - 1.1 = (2.04)\) (seen anywhere) (A1)
choosing cosine rule (M1)
correct substitution A1
e.g. \({\rm{O}}{{\rm{D}}^2} = {9.71^2} + {4^2} - 2 \times 9.71 \times 4 \times \cos (\pi - 1.1)\)
\({\text{OD}} = 12.1{\text{ (cm)}}\) A1 N3
METHOD 2
finding angle \({\rm{OAD}} = \pi - 1.1 = (2.04)\) (seen anywhere) (A1)
choosing sine rule (M1)
correct substitution A1
e.g. \(\frac{{{\rm{OD}}}}{{\sin (\pi - 1.1)}} = \frac{{9.71}}{{\sin 0.8}} = \frac{4}{{\sin 0.3}}\)
\({\text{OD}} = 12.1{\text{ (cm)}}\) A1 N3
[4 marks]
correct substitution into area of a sector formula (A1)
e.g. \({\rm{area}} = 0.5 \times {4^2} \times 0.8\)
\({\text{area}} = 6.4{\text{ (c}}{{\text{m}}^2}{\text{)}}\) A1 N2
[2 marks]
substitution into area of triangle formula OAD (M1)
correct substitution A1
e.g. \(A{\rm{ = }}\frac{1}{2} \times 4 \times 12.1 \times \sin 0.8\) , \(A{\rm{ = }}\frac{1}{2} \times 4 \times 9.71 \times \sin 2.04\) , \(A{\rm{ = }}\frac{1}{2} \times 12.1 \times 9.71 \times \sin 0.3\)
subtracting area of sector OABC from area of triangle OAD (M1)
e.g. \({\text{area ABCD}} = 17.3067 - 6.4\)
\({\text{area ABCD}} = 10.9{\text{ (c}}{{\text{m}}^2}{\text{)}}\) A1 N2
[4 marks]
Examiners report
This question was generally quite well done, and it was pleasing to note that candidates could come up with multiple methods to arrive at the correct answers. Many candidates worked comfortably with the sine and cosine rules to find sides of triangles. Some candidates chose alternative right-angled triangle methods, often with success, although this proved a time-consuming approach. Some unnecessarily converted the radian values to degrees, which sometimes led to calculation errors that could have been avoided. A large number of candidates accrued the accuracy penalty in this question.
This question was generally quite well done, and it was pleasing to note that candidates could come up with multiple methods to arrive at the correct answers. Many candidates worked comfortably with the sine and cosine rules to find sides of triangles. Some candidates chose alternative right-angled triangle methods, often with success, although this proved a time-consuming approach. Some unnecessarily converted the radian values to degrees, which sometimes led to calculation errors that could have been avoided. A large number of candidates accrued the accuracy penalty in this question.
This question was generally quite well done, and it was pleasing to note that candidates could come up with multiple methods to arrive at the correct answers. Many candidates worked comfortably with the sine and cosine rules to find sides of triangles. Some candidates chose alternative right-angled triangle methods, often with success, although this proved a time-consuming approach. Some unnecessarily converted the radian values to degrees, which sometimes led to calculation errors that could have been avoided. A large number of candidates accrued the accuracy penalty in this question.
This question was generally quite well done, and it was pleasing to note that candidates could come up with multiple methods to arrive at the correct answers. Many candidates worked comfortably with the sine and cosine rules to find sides of triangles. Some candidates chose alternative right-angled triangle methods, often with success, although this proved a time-consuming approach. Some unnecessarily converted the radian values to degrees, which sometimes led to calculation errors that could have been avoided. A large number of candidates accrued the accuracy penalty in this question.

