In this page, we will will learn about the Pythagorean Identities. It is actually quite rare that exam questions are solely about these identities, but it is essential that you can use and manipulate them confidently because they are used in so many different parts of the course (so they do come up a lot!). You will learn what they are and how to use them.
On this page, you should learn about
the Pythagorean identity \(\large \cos^{ 2 }\theta +\sin^{ 2 }\theta \equiv 1\) This quiz is about the Pythagorean Identity sin²x + cos²x \(\equiv\) 1
Thinking about the trigonometric identities, which of the following is true?
Select all
The only 2 statements that are true come from the Pythagorean Trigonometric identity sin²x + cos²x \(\equiv\) 1
Thinking about the trigonometric identities, which of the following is true?
Select all
The only 2 statements that are true come from the Pythagorean Trigonometric identity sin²x + cos²x \(\equiv\) 1
Use the trigonometric identity sin²x + cos²x \(\equiv\) 1
sin²x \(\equiv\) 1 - cos²x
sin²x = 1 - 0.7²
= 1 - 0.49
= 0.51
f(x) = sin²x + cos²x
sin²x + cos²x \(\equiv\) 1
Therefore,
f(x) = 1
Write 3sin²x + 4cos²x in terms of cosx only
Use the trigonometric identity sin²x + cos²x \(\equiv\) 1
3sin²x + 4cos²x
\(\equiv\) 3(1 - cos²x) + 4 cos²x
\(\equiv\) 3 - 3cos²x + 4 cos²x
\(\equiv\) 3 + cos²x
Write 2cos²x - 3sin²x in terms of sinx only
Use the trigonometric identity sin²x + cos²x \(\equiv\) 1 ?
2cos²x - 3sin²x
\(\equiv\) 2(1 - sin²x) - 3sin²x
\(\equiv\) 2 - 2sin²x - 3sin²x
\(\equiv\) 2 - 5sin²x
Which of the following is equivalent to (sinx - cosx)² ?
Use the trigonometric identity sin²x + cos²x \(\equiv\) 1
(sinx - cosx)²
\(\equiv\) (sinx - cosx)(sinx - cosx)
\(\equiv\) sin²x - 2sinxcosx + cos²x
\(\equiv\) 1 - 2sinxcosx
\(\equiv\) 1 - sin2x
For the last step, we use the double ange for sin2x
sin2x \(\equiv\) 2sinxcosx
Which of the following is equivalent to cosx + tanxsinx?
We use the following 2 identities
tanx \(\equiv \frac{sinx}{cosx}\)
sin²x + cos²x \(\equiv\) 1
cosx + tanxsinx
\(\equiv cosx + \frac{sinx}{cosx}sinx\)
\(\equiv \frac{cos²x}{cosx}+ \frac{sin²x}{cosx}\)
\(\equiv \frac{cos²x +sin²x}{cosx}\)
\(\equiv \frac{1}{cosx}\)
\(\equiv\) secx
Which of the following is identically equal to 2sin²x - 5cos²x
Select all
We use the trigonometric identity sin²x + cos²x \(\equiv\) 1
There are two correct identities
Answer 1 2sin²x - 5cos²x \(\equiv\) 2(1 - cos²x) - 5 cos²x
\(\equiv\) 2 - 2cos²x - 5cos²x
\(\equiv\) 2 - 7cos²x
Answer 2
2sin²x - 5cos²x \(\equiv\) 2sin²x - 5(1 - sin²x)
\(\equiv\) 2sin²x - 5 + 5sin²x
\(\equiv\) 7sin²x - 5
Which of the following is identically equal to \(\frac{cosx}{1+sinx}-\frac{1-sinx}{cosx}\)
There is only one
We use the trigonometric identity sin²x + cos²x \(\equiv\) 1
Add the fractions together by making the denominator the same
\(\frac{cosx}{1+sinx}-\frac{1-sinx}{cosx}\equiv\frac{cos²x}{(1+sinx)cosx}-\frac{(1-sinx)(1+sinx)}{(1+sinx)cosx}\)
\(\equiv\frac{cos²x}{(1+sinx)cosx}-\frac{1+sinx-sinx-sin²x}{(1+sinx)cosx}\)
\(\equiv\frac{cos²x}{(1+sinx)cosx}-\frac{1-sin²x}{(1+sinx)cosx}\)
\(\equiv\frac{cos²x-1+sin²x}{(1+sinx)cosx}\)
\(\equiv\frac{1-1}{(1+sinx)cosx}\)
\(\equiv0\)
a) Show that the equation \(\large 2 \sin^2x=3 \cos x\) may be written in the form
\(\large 2 \cos^2x+3 \cos x-2=0\)
b) Hence , solve \(\large 2 \sin^2x=3 \cos x\) , for \(\large 0\le x\le2\pi\)
a) Use \(\large \cos^2 x+\sin ^2x\equiv1\)
b) Use the answer from part a). This is a quadratic equation.
Don't forget that \(\large \cos^2 x\) means \(\large (\cos x)^2\)
Given that \(x=\frac{2}{cos\theta}\) and \(y=3tan\theta\)
show that \(\frac{x^2}{4}-\frac{y^2}{9}=1\)
\(\tan^2\theta=\frac{sin²\theta}{cos²\theta}\)
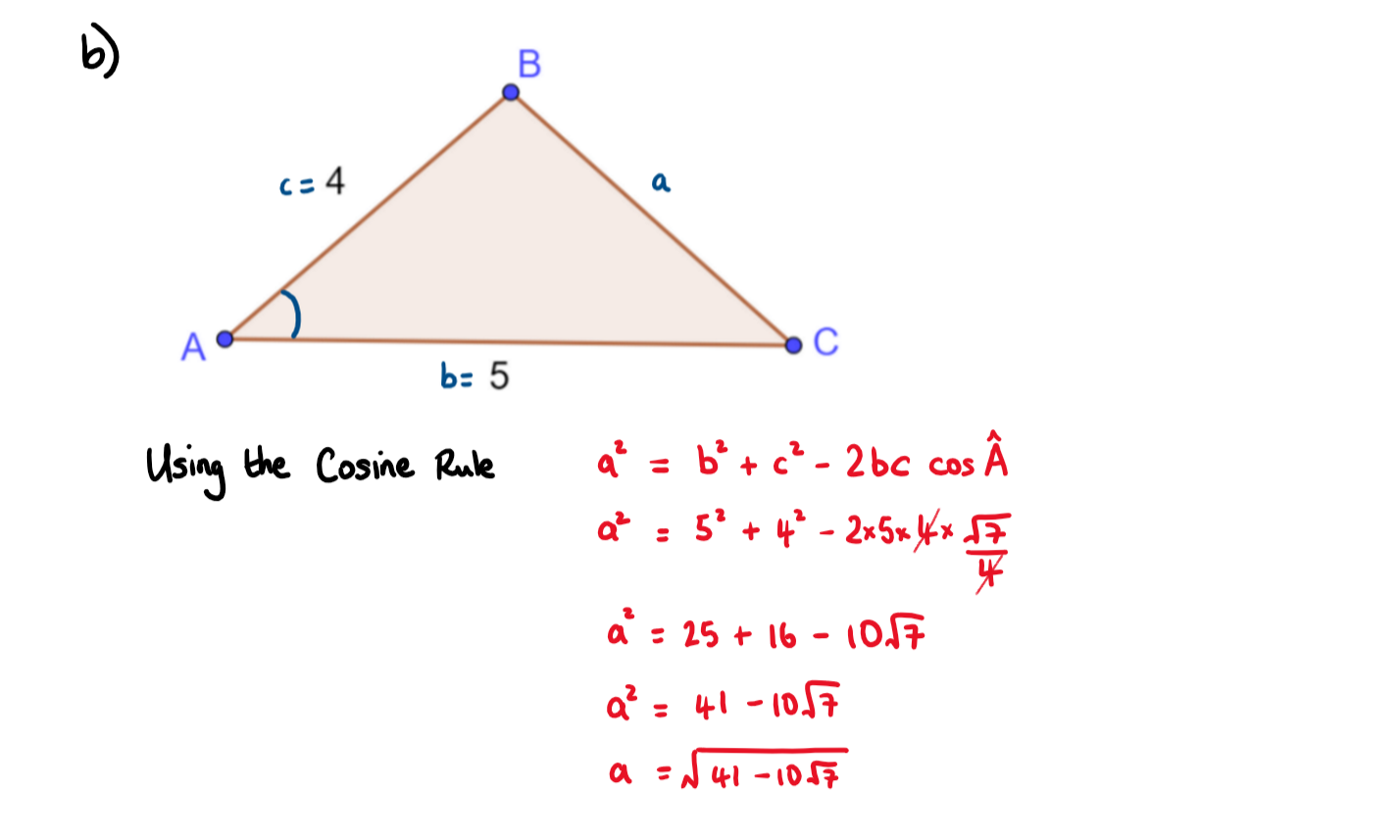
The following diagram shows triangle ABC with AB = 4 and AC = 5
DIAGRAM NOT TO SCALE
a) Given that \(\large \sin \hat A=\frac{3}{4}\) , find the value of \(\large \cos \hat A\)
b) Hence , show that the length of \(\large BC=\sqrt{41-10\sqrt{7}}\)
a) You can use the Pythagorean identity \(\large \cos^2\theta+\sin^2\theta\equiv1\) \(\large \cos \hat A\)
b) Use the Cosine Rule, c ² = a² + b ² - 2ab cosC
Prove that \(\large \frac{\sin ^3\theta}{\tan \theta}+\cos^3\theta\equiv\cos\theta\)
This is a very difficult proof for SL students!
There is always more than one way to carry out this proof.
The easiest, is to start with the left hand side and consider that \(\large \tan\theta\equiv\frac{\sin\theta}{\cos\theta}\)
MY PROGRESS
Self-assessment How much of Pythagorean Identity SL have you understood?
My notes
Which of the following best describes your feedback?



 Given that cosx = 0.7 , work out sin²x
Given that cosx = 0.7 , work out sin²x

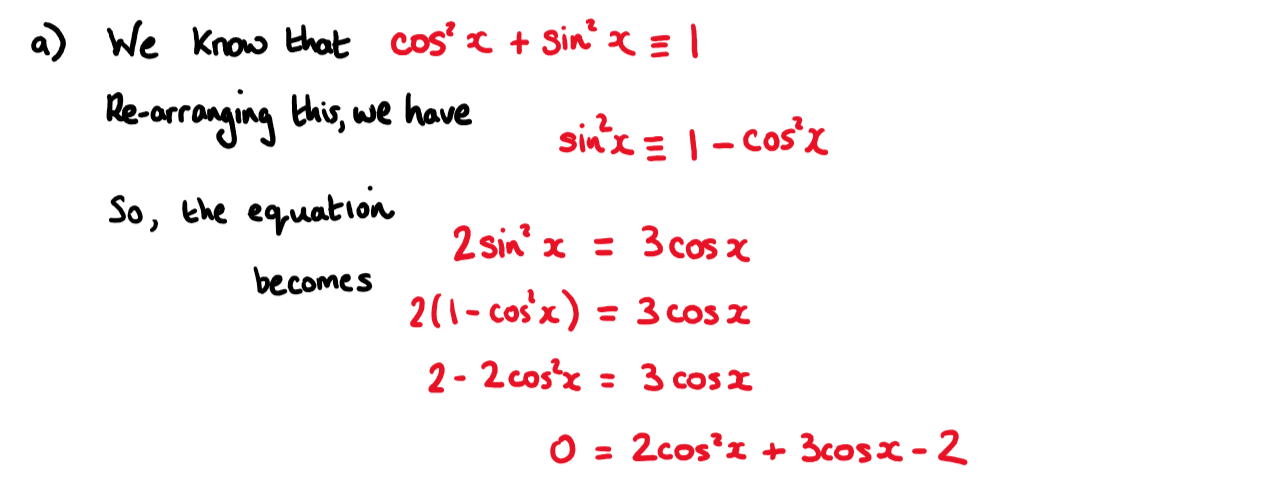

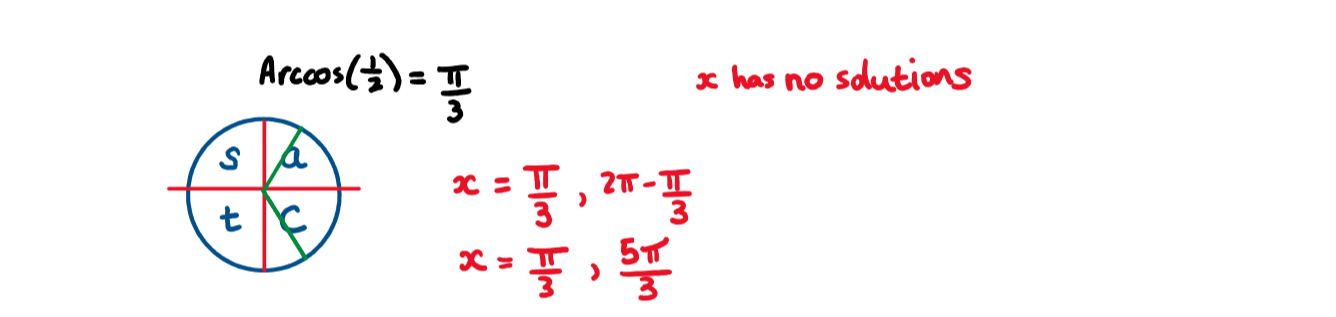


 DIAGRAM NOT TO SCALE
DIAGRAM NOT TO SCALE
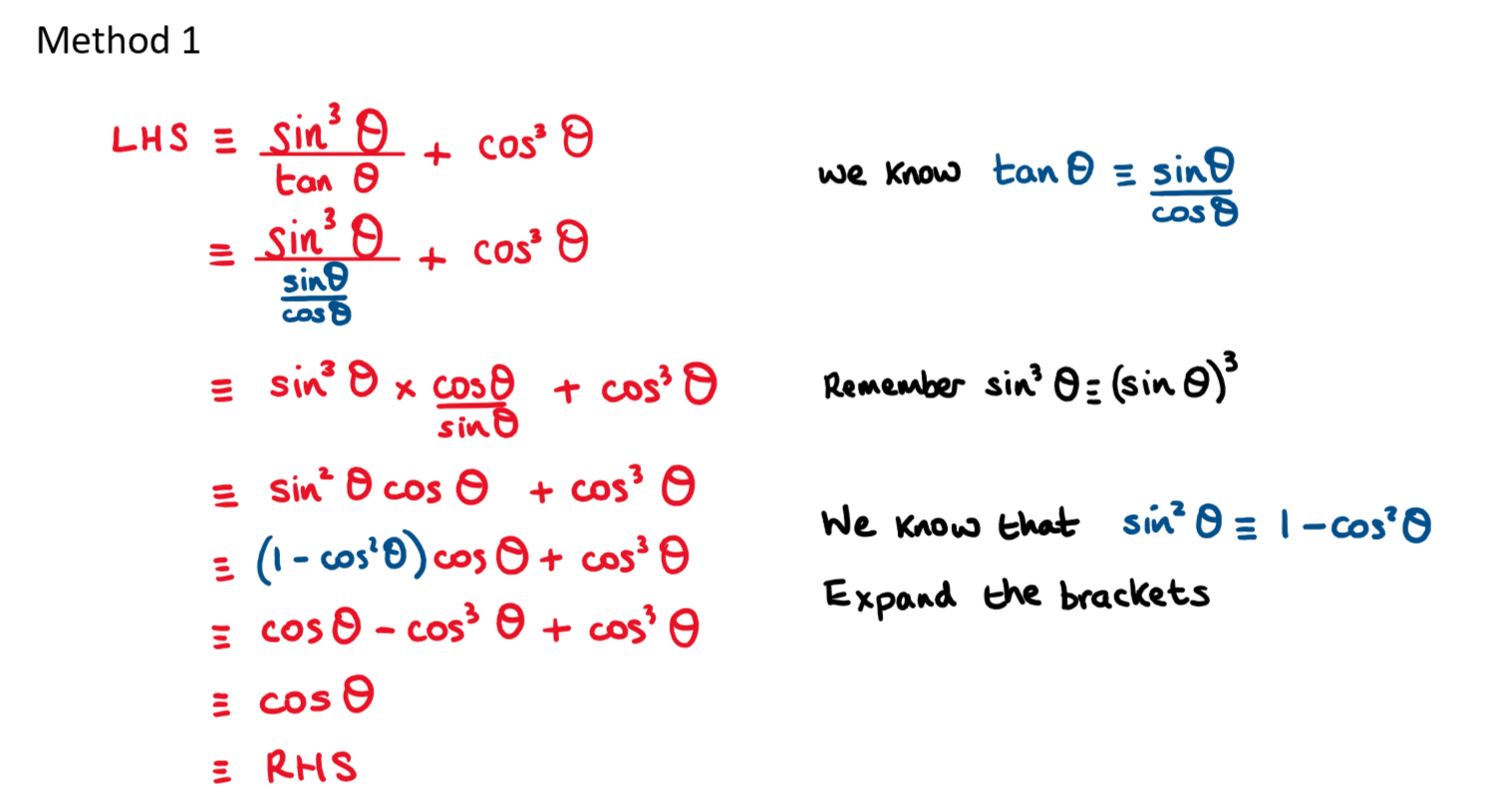
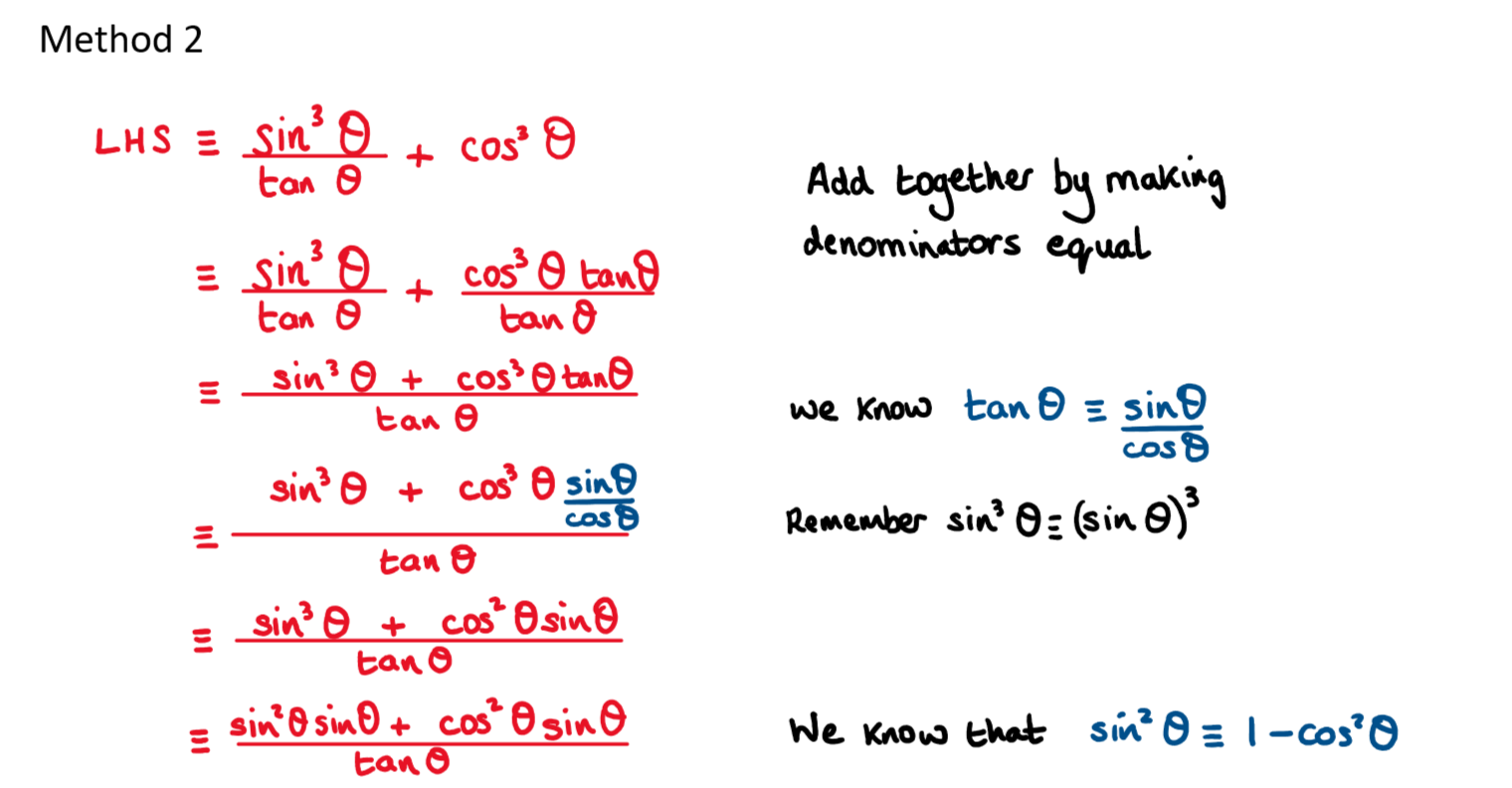

 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn