| Date | November 2010 | Marks available | 9 | Reference code | 10N.2.hl.TZ0.6 |
| Level | HL | Paper | 2 | Time zone | TZ0 |
| Command term | Deduce, Determine, and State and explain | Question number | 6 | Adapted from | N/A |
Question
The Haber process enables the large-scale production of ammonia needed to make fertilizers.
The equation for the Haber process is given below.
\[{{\text{N}}_2}({\text{g)}} + 3{{\text{H}}_2}({\text{g)}} \rightleftharpoons {\text{2N}}{{\text{H}}_3}({\text{g)}}\]
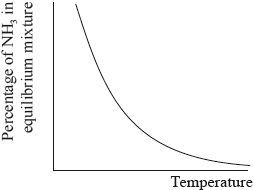
The percentage of ammonia in the equilibrium mixture varies with temperature.
Ammonia can be converted into nitric acid, \({\text{HN}}{{\text{O}}_{\text{3}}}{\text{(aq)}}\), and hydrocyanic acid, HCN(aq). The \({\text{p}}{K_{\text{a}}}\) of hydrocyanic acid is 9.21.
A student decided to investigate the reactions of the two acids with separate samples of \({\text{0.20 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sodium hydroxide solution.
(i) Use the graph to deduce whether the forward reaction is exothermic or endothermic and explain your choice.
(ii) State and explain the effect of increasing the pressure on the yield of ammonia.
(iii) Deduce the equilibrium constant expression, \({K_{\text{c}}}\), for the reaction.
(iv) A mixture of 1.00 mol \({{\text{N}}_{\text{2}}}\) and 3.00 mol \({{\text{H}}_{\text{2}}}\) was placed in a \({\text{1.0 d}}{{\text{m}}^{\text{3}}}\) flask at 400 °C. When the system was allowed to reach equilibrium, the concentration of was found to be \({\text{0.062 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\). Determine the equilibrium constant, \({K_{\text{c}}}\), of the reaction at this temperature.
(v) Iron is used as a catalyst in the Haber process. State the effect of a catalyst on the value of \({K_{\text{c}}}\).
(i) Distinguish between the terms strong and weak acid and state the equations used to show the dissociation of each acid in aqueous solution.
(ii) Deduce the expression for the ionization constant, \({K_{\text{a}}}\), of hydrocyanic acid and calculate its value from the \({\text{p}}{K_{\text{a}}}\) value given.
(iii) Use your answer from part (b) (ii) to calculate the \({\text{[}}{{\text{H}}^ + }{\text{]}}\) and the pH of an aqueous solution of hydrocyanic acid of concentration \({\text{0.108 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\). State one assumption made in arriving at your answer.
A small piece of magnesium ribbon is added to solutions of nitric and hydrocyanic acid of the same concentration at the same temperature. Describe two observations that would allow you to distinguish between the two acids.
(i) Calculate the volume of the sodium hydroxide solution required to react exactly with a \({\text{15.0 c}}{{\text{m}}^{\text{3}}}\) solution of \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) nitric acid.
(ii) The following hypothesis was suggested by the student: “Since hydrocyanic acid is a weak acid it will react with a smaller volume of the \({\text{0.20 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sodium hydroxide solution.” Comment on whether or not this is a valid hypothesis.
(iii) Use Table 16 of the Data Booklet to identify a suitable indicator for the titration of sodium hydroxide and hydrocyanic acid.
Markscheme
(i) exothermic;
Accept either of the following for the second mark.
increasing temperature favours endothermic/reverse reaction;
as yield decreases with increasing temperature;
(ii) yield increases / equilibrium moves to the right / more ammonia;
increase in pressure favours the reaction which has fewer moles of gaseous products;
(iii) \({K_{\text{c}}} = \frac{{{{{\text{[N}}{{\text{H}}_3}{\text{]}}}^2}}}{{{\text{[}}{{\text{N}}_2}{\text{][}}{{\text{H}}_2}{{\text{]}}^3}}}\);
(iv) \({\text{[}}{{\text{N}}_2}{\text{]}}\): (at equilibrium \( = 1.00 - 0.031 = \)) \({\text{0.969 (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
\({\text{[}}{{\text{H}}_2}{\text{]}}\): (at equilibrium \( = 3.00 - 3(0.031) = \)) \({\text{2.91 (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
\({K_{\text{c}}}{\text{ }}\left( { = \frac{{{{{\text{(0.062)}}}^2}}}{{{\text{(0.969) (2.91}}{{\text{)}}^3}}}} \right) = {\text{1.6(1)}} \times {\text{1}}{{\text{0}}^{ - 4}}\);
Ignore units.
Award [1] for Kc = 1.4 \( \times \) 10–4
(v) no effect;
(i) strong acid completely dissociated/ionized and weak acid partially dissociated/ionized;
\({\text{HN}}{{\text{O}}_3}{\text{(aq)}} \to {{\text{H}}^ + }{\text{(aq)}} + {\text{NO}}_3^ - {\text{(aq)}}\);
\({\text{HCN(aq)}} \rightleftharpoons {{\text{H}}^ + }{\text{(aq)}} + {\text{C}}{{\text{N}}^ - }{\text{(aq)}}\);
Insist on both arrows as shown.
State symbols not needed.
Accept H2O and H3O+.
(ii) \({K_{\text{a}}} = \frac{{{\text{[}}{{\text{H}}^ + }{\text{][C}}{{\text{N}}^ - }{\text{]}}}}{{{\text{[HCN]}}}}\);
Allow H3O+ instead of H+.
\({K_{\text{a}}} = {10^{ - 9.21}} = 6.17 \times {10^{ - 10}}\);
(iii) \({[{{\text{H}}^ + }] = \sqrt {{K_{\text{a}}}[{\text{HCN}}]} /\sqrt {(6.17 \times {{10}^{ - 10}} \times 0.108)} }\);
\({ = 8.16 \times {{10}^{ - 6}}}\);
Allow in the range 8.13 \( \times \) 10–6 to 8.16 \( \times \) 10–6.
\({\text{pH}} = 5.09\);
OR
\({{\text{pH}} = \frac{1}{2}{\text{(p}}{K_{\text{a}}} - {\text{log}}[{\text{HCN}}])/\frac{1}{2}(9.21 - \log \,0.108)}\);
\({ = 5.09}\);
\({\text{[}}{{\text{H}}^ + }{\text{]}} = {10^{ - 5.09}} = 8.16 \times {10^{ - 6}}\);
Allow in the range 8.13 \( \times \) 10–6 to 8.16 \( \times \) 10–6.
If expression for [H+] missing but both answers correct, award [3], if one answer
correct, award [2].
assume \({\text{[}}{{\text{H}}^ + }{\text{]}} \ll 0.108\) / negligible dissociation;
With HNO3:
faster rate of bubble/hydrogen/gas production;
faster rate of magnesium dissolving;
higher temperature change;
Accept opposite argument for HCN.
Reference to specific observations needed.
Award [1] if 2 observations given but acid is not identified.
(i) (nitric acid) 7.5 cm3;
(ii) not valid as hydrocyanic acid reacts with same volume/ 7.5 cm3;
(iii) bromothymol blue / phenol red / phenolphthalein;
Examiners report
Equilibrium is a topic that has shown substantial improvement in recent sessions with some very well produced arguments. The reaction was correctly described as exothermic with a reason correctly given in most cases. Most candidates knew that yield would increase with increased pressure, but some failed to identify the change in the number of “gaseous” molecules as the reason. More candidates had difficulty with the equilibrium constant calculation often using the initial not equilibrium concentrations.
In (b) most correctly defined strong and weak acids and many also wrote correct equations. A few, however, missed the equilibrium sign for hydrocyanic acid. HA, CH3COOH and HCl were commonly given instead of HCN and HNO3, suggesting that students sometimes have difficulty applying general concepts to specific cases. It was encouraging to see many candidates determine the pH from the pKa value including the assumption that there is negligible dissociation, as this has challenged students in previous sessions. A significant number of weaker candidates reported however that the acid solution would have pH values above 7.
Part (c) presented problems with many candidates unable to describe specific observations related to rate which would distinguish between a strong and weak acid and simply stated that the reaction would be faster.
The moles calculation was answered well in (d) with most candidates able to identify phenolphthalein as a suitable indicator.

