| Date | May 2014 | Marks available | 3 | Reference code | 14M.2.hl.TZ2.6 |
| Level | HL | Paper | 2 | Time zone | TZ2 |
| Command term | Predict and State | Question number | 6 | Adapted from | N/A |
Question
A group of students investigated the rate of the reaction between aqueous sodium thiosulfate and hydrochloric acid according to the equation below.
\[{\text{N}}{{\text{a}}_2}{{\text{S}}_2}{{\text{O}}_3}{\text{(aq)}} + {\text{2HCl(aq)}} \to {\text{2NaCl(aq)}} + {\text{S}}{{\text{O}}_2}{\text{(g)}} + {\text{S(s)}} + {{\text{H}}_2}{\text{O(l )}}\]
The two reagents were rapidly mixed together in a beaker and placed over a mark on a piece of paper. The time taken for the precipitate of sulfur to obscure the mark when viewed through the reaction mixture was recorded.
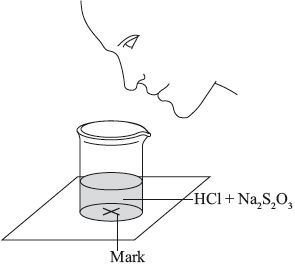
Initially they measured out \({\text{10.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.500 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) hydrochloric acid and then added \({\text{40.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.0200 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) aqueous sodium thiosulfate. The mark on the paper was obscured 47 seconds after the solutions were mixed.
One proposed mechanism for this reaction is:
\({{\text{S}}_2}{\text{O}}_3^{2 - }{\text{(aq)}} + {{\text{H}}^ + }{\text{(aq)}} \rightleftharpoons {\text{H}}{{\text{S}}_2}{\text{O}}_3^ - {\text{(aq)}}\) Fast
\({\text{H}}{{\text{S}}_2}{\text{O}}_3^ - {\text{(aq)}} + {{\text{H}}^ + }{\text{(aq)}} \to {\text{S}}{{\text{O}}_2}{\text{(g)}} + {\text{S(s)}} + {{\text{H}}_2}{\text{O(l)}}\) Slow
The teacher asked the students to devise another technique to measure the rate of this reaction.
Another group suggested collecting the sulfur dioxide and drawing a graph of the volume of gas against time.
(i) State the volumes of the liquids that should be mixed.

(ii) State why it is important that the students use a similar beaker for both reactions.
(iii) If the reaction were first order with respect to the thiosulfate ion, predict the time it would take for the mark on the paper to be obscured when the concentration of sodium thiosulfate solution is halved.
(i) Deduce the rate expression of this mechanism.
(ii) The results of an experiment investigating the effect of the concentration of hydrochloric acid on the rate, while keeping the concentration of thiosulfate at the original value, are given in the table below.

On the axes provided, draw an appropriate graph to investigate the order of the reaction with respect to hydrochloric acid.
(iii) Identify two ways in which these data do not support the rate expression deduced in part (i).
(i) Sketch and label, indicating an approximate activation energy, the Maxwell–Boltzmann energy distribution curves for two temperatures, \({T_1}\) and \(T2{\text{ }}({T_2} > {T_1})\), at which the rate of reaction would be significantly different.

(ii) Explain why increasing the temperature of the reaction mixture would significantly increase the rate of the reaction.
(i) One group suggested recording how long it takes for the pH of the solution to change by one unit. Calculate the initial pH of the original reaction mixture.
(ii) Deduce the percentage of hydrochloric acid that would have to be used up for the pH to change by one unit.
Calculate the volume of sulfur dioxide, in \({\text{c}}{{\text{m}}^{\text{3}}}\), that the original reaction mixture would produce if it were collected at \(1.00 \times {10^5}{\text{ Pa}}\) and 300 K.
Sulfur dioxide, a major cause of acid rain, is quite soluble in water and the equilibrium shown below is established.
\({\text{S}}{{\text{O}}_2}{\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {\text{HSO}}_3^ - {\text{(aq)}} + {{\text{H}}^ + }{\text{(aq)}}\)
Given that the \({K_{\text{a}}}\) for this equilibrium is \(1.25 \times {10^{ - 2}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\), determine the pH of a \(2.00{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) solution of sulfur dioxide.
Using Table 15 of the Data Booklet, identify an organic acid that is a stronger acid than sulfur dioxide.
Markscheme
(i)  ;
;
Accept other volumes in a 1:2:2 ratio.
(ii) depth of liquid in the beaker must remain constant / OWTTE;
Accept “same thickness of glass” and any other valid point, such as answers framed around minimizing uncontrolled variables / making it a “fair test”.
(iii) 94 (s) / 1 min 34 s;
(i) \({\text{rate}} = k{\text{[}}{{\text{S}}_{\text{2}}}{\text{O}}_3^{2 - }{\text{][}}{{\text{H}}^ + }{{\text{]}}^2}/{\text{rate}} = k{\text{[N}}{{\text{a}}_2}{{\text{S}}_2}{{\text{O}}_3}{\text{][HCl}}{{\text{]}}^2}\);
(ii) 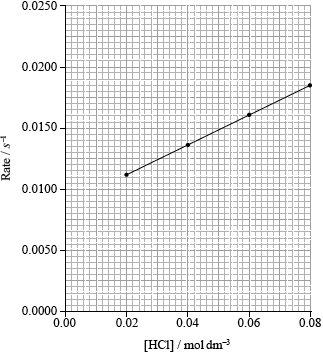
correct scale and units on y-axis;
Accept other suitable scales (such as 1/t) and units (such as ms–1).
Axes do not have to show origin/start at zero.
correct calculation of rate in \({s^{ - 1}}\);

If graph correct, assume this has been done on calculator and not written down.
correct plotting of points that the student decides to use and a connecting line;
Award final mark if 3 or more points are correct, irrespective of what is plotted on y-axis.
If line goes through the correct values at given concentrations of HCl, assume that points are marked there.
(iii) linear dependence on [HCl] (so not second order in \({\text{[}}{{\text{H}}^ + }{\text{]}}\));
Accept that doubling of concentration does not result in quadrupling of rate / OWTTE.
does not go through origin;
Remember to allow ECF from (b) (i).
(i) 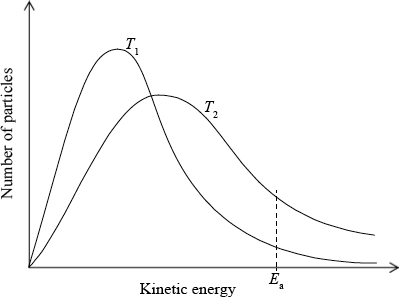
labelled y-axis: number of particles / probability of particles (with that kinetic energy) and labelled x-axis: (kinetic) energy;
Allow fraction/proportion/amount of particles (with kinetic energy) for y-axis label.
Allow speed/velocity for x-axis label.
\({T_2}\) curve broader and with maximum lower and to right of \({T_1}\) curve;
Do not award this mark if both curves not asymmetric.
Curves must pass through the origin and be asymptotic to x axis.
Do not award this mark if curves not labelled.
\({E_{\text{a}}}\) marked on graph;
(ii) kinetic energy of molecules increases;
This may be answered implicitly in the final marking point.
frequency of collision/number of collisions per unit time increases;
Do not accept “number of collisions increases”.
greater proportion of molecules have energy greater than/equal to activation energy / rate related to temperature by the Arrhenius equation;
Award [1 max] for statements such as “there will be more successful collisions” if neither of last two marking points awarded.
(i) \({\text{[}}{{\text{H}}^ + }{\text{]}} = 0.5 \times \frac{{10}}{{50}} = 0.1{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
\({\text{pH (}} = - \log {\text{[H}}{{\text{r}}^ + }{\text{]}} = - \log (0.10)) = 1\);
(ii) 90%;
\({\text{mol N}}{{\text{a}}_{\text{2}}}{{\text{S}}_{\text{2}}}{{\text{O}}_{\text{3}}} = {\text{mol S}}{{\text{O}}_{\text{2}}} = 0.0400 \times 0.0200 = 0.000800\);
\(V = \frac{{n \times R \times T}}{p}/\frac{{0.000800 \times 8.31 \times 300}}{{{{10}^5}}}\);
\((1.99 \times {10^{ - 5}}{\text{ }}{{\text{m}}^3}) = 19.9{\text{ }}({\text{c}}{{\text{m}}^3})\);
Note that two errors involving a factor of 1000 can also produce the correct answer. If this is the case award [1] not [3].
Accept 20.0 cm3 if R =8.314 is used.
Award [2] for 17.9 cm3 or 19.2 cm3 (result from using molar volume at standard temperature and pressure or at room temperature and pressure).
OR
\({\text{mol N}}{{\text{a}}_2}{{\text{S}}_2}{{\text{O}}_3} = {\text{mol S}}{{\text{O}}_2} = 0.0400 \times 0.0200 = 0.000800\);
\(V = 0.00080 \times 2.24 \times {10^{ - 2}} \times \left[ {\frac{{1.00 \times {{10}^5}}}{{1.01 \times {{10}^5}}}} \right] \times \frac{{300}}{{273}}\);
\((1.95 \times {10^{ - 5}}{\text{ }}{{\text{m}}^3}) = 19.5{\text{ }}({\text{c}}{{\text{m}}^3})\);
Note that two errors involving a factor of 1000 can also produce the correct answer. If this is the case award [1] not [3].
Deduct [1] for answers based on amount of HCl, so correct calculation would score [2 max].
\({K_{\text{a}}} = \frac{{{\text{[}}{{\text{H}}^ + }{\text{][HSO}}_3^ - {\text{]}}}}{{{\text{[}}{{\text{H}}_2}{\text{S}}{{\text{O}}_3}{\text{]}}}} = \frac{{{x^2}}}{{2 - x}} \approx \frac{{{x^2}}}{2} \approx 1.25 \times {10^{ - 2}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
\({\text{[}}{{\text{H}}^ + }{\text{]}} = \sqrt {2.50 \times {{10}^{ - 2}}} = 0.158{\text{ }}({\text{mol}}\,{\text{d}}{{\text{m}}^{ - 3}})\);
\({\text{pH}} = - \log (0.158) = 0.80\);
Award [3] for correct final answer.
dichloroethanoic acid / trichloroethanoic acid / 2,4,6-trinitrophenol;
Examiners report
This was quite a popular question, though generally not well answered. In the first part students again appeared to display a lack of expertise in a practical context with very few able to devise a mixture that would halve the concentration of thiosulfate, whilst keeping other concentrations constant, and answers predicting that this would halve the reaction time were far more commonly encountered than those doubling it. Many candidates did however suggest valid reasons why the reaction vessel should remain unchanged and a significant number of students were able to correctly deduce the rate equation that the mechanism given would predict. Again a lack of ability to interpret experimental data was evident in the fact that it was very rare to find students who realised that a graph of (time)-1 against concentration was required to be able to deduce the reaction order, with almost all simply plotting time-concentration graphs and, as a result, very few could evaluate the mechanism in the light of the experimental data. Part (c) was a fairly standard question on the effect of temperature on reaction rate, hence it was a surprise that students did not score better on it, with many of the oft repeated mistakes (number of collisions rather than collision frequency) again coming to the surface. Again it was probably inability to interpret experimental data that led to only very few students being able to correctly state the initial pH of the mixture (I am certain almost all would have gained the mark if the pH of \({\text{ 0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) HCl had been asked for) and the percentage that would have to be consumed to increase the pH by one unit (which is independent of the previous answer) proved too much for almost all candidates. In part (e) most students could quote and substitute into the ideal gas equation, but converting from \({{\text{m}}^3}\) to \({\text{c}}{{\text{m}}^3}\) posed a problem for most candidates. Quite a number of candidates were however able to calculate the pH of the sulfur dioxide solution and identify a stronger acid.
This was quite a popular question, though generally not well answered. In the first part students again appeared to display a lack of expertise in a practical context with very few able to devise a mixture that would halve the concentration of thiosulfate, whilst keeping other concentrations constant, and answers predicting that this would halve the reaction time were far more commonly encountered than those doubling it. Many candidates did however suggest valid reasons why the reaction vessel should remain unchanged and a significant number of students were able to correctly deduce the rate equation that the mechanism given would predict. Again a lack of ability to interpret experimental data was evident in the fact that it was very rare to find students who realised that a graph of (time)-1 against concentration was required to be able to deduce the reaction order, with almost all simply plotting time-concentration graphs and, as a result, very few could evaluate the mechanism in the light of the experimental data. Part (c) was a fairly standard question on the effect of temperature on reaction rate, hence it was a surprise that students did not score better on it, with many of the oft repeated mistakes (number of collisions rather than collision frequency) again coming to the surface. Again it was probably inability to interpret experimental data that led to only very few students being able to correctly state the initial pH of the mixture (I am certain almost all would have gained the mark if the pH of \({\text{ 0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) HCl had been asked for) and the percentage that would have to be consumed to increase the pH by one unit (which is independent of the previous answer) proved too much for almost all candidates. In part (e) most students could quote and substitute into the ideal gas equation, but converting from \({{\text{m}}^3}\) to \({\text{c}}{{\text{m}}^3}\) posed a problem for most candidates. Quite a number of candidates were however able to calculate the pH of the sulfur dioxide solution and identify a stronger acid.
This was quite a popular question, though generally not well answered. In the first part students again appeared to display a lack of expertise in a practical context with very few able to devise a mixture that would halve the concentration of thiosulfate, whilst keeping other concentrations constant, and answers predicting that this would halve the reaction time were far more commonly encountered than those doubling it. Many candidates did however suggest valid reasons why the reaction vessel should remain unchanged and a significant number of students were able to correctly deduce the rate equation that the mechanism given would predict. Again a lack of ability to interpret experimental data was evident in the fact that it was very rare to find students who realised that a graph of (time)-1 against concentration was required to be able to deduce the reaction order, with almost all simply plotting time-concentration graphs and, as a result, very few could evaluate the mechanism in the light of the experimental data. Part (c) was a fairly standard question on the effect of temperature on reaction rate, hence it was a surprise that students did not score better on it, with many of the oft repeated mistakes (number of collisions rather than collision frequency) again coming to the surface. Again it was probably inability to interpret experimental data that led to only very few students being able to correctly state the initial pH of the mixture (I am certain almost all would have gained the mark if the pH of \({\text{ 0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) HCl had been asked for) and the percentage that would have to be consumed to increase the pH by one unit (which is independent of the previous answer) proved too much for almost all candidates. In part (e) most students could quote and substitute into the ideal gas equation, but converting from \({{\text{m}}^3}\) to \({\text{c}}{{\text{m}}^3}\) posed a problem for most candidates. Quite a number of candidates were however able to calculate the pH of the sulfur dioxide solution and identify a stronger acid.
This was quite a popular question, though generally not well answered. In the first part students again appeared to display a lack of expertise in a practical context with very few able to devise a mixture that would halve the concentration of thiosulfate, whilst keeping other concentrations constant, and answers predicting that this would halve the reaction time were far more commonly encountered than those doubling it. Many candidates did however suggest valid reasons why the reaction vessel should remain unchanged and a significant number of students were able to correctly deduce the rate equation that the mechanism given would predict. Again a lack of ability to interpret experimental data was evident in the fact that it was very rare to find students who realised that a graph of (time)-1 against concentration was required to be able to deduce the reaction order, with almost all simply plotting time-concentration graphs and, as a result, very few could evaluate the mechanism in the light of the experimental data. Part (c) was a fairly standard question on the effect of temperature on reaction rate, hence it was a surprise that students did not score better on it, with many of the oft repeated mistakes (number of collisions rather than collision frequency) again coming to the surface. Again it was probably inability to interpret experimental data that led to only very few students being able to correctly state the initial pH of the mixture (I am certain almost all would have gained the mark if the pH of \({\text{ 0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) HCl had been asked for) and the percentage that would have to be consumed to increase the pH by one unit (which is independent of the previous answer) proved too much for almost all candidates. In part (e) most students could quote and substitute into the ideal gas equation, but converting from \({{\text{m}}^3}\) to \({\text{c}}{{\text{m}}^3}\) posed a problem for most candidates. Quite a number of candidates were however able to calculate the pH of the sulfur dioxide solution and identify a stronger acid.
This was quite a popular question, though generally not well answered. In the first part students again appeared to display a lack of expertise in a practical context with very few able to devise a mixture that would halve the concentration of thiosulfate, whilst keeping other concentrations constant, and answers predicting that this would halve the reaction time were far more commonly encountered than those doubling it. Many candidates did however suggest valid reasons why the reaction vessel should remain unchanged and a significant number of students were able to correctly deduce the rate equation that the mechanism given would predict. Again a lack of ability to interpret experimental data was evident in the fact that it was very rare to find students who realised that a graph of (time)-1 against concentration was required to be able to deduce the reaction order, with almost all simply plotting time-concentration graphs and, as a result, very few could evaluate the mechanism in the light of the experimental data. Part (c) was a fairly standard question on the effect of temperature on reaction rate, hence it was a surprise that students did not score better on it, with many of the oft repeated mistakes (number of collisions rather than collision frequency) again coming to the surface. Again it was probably inability to interpret experimental data that led to only very few students being able to correctly state the initial pH of the mixture (I am certain almost all would have gained the mark if the pH of \({\text{ 0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) HCl had been asked for) and the percentage that would have to be consumed to increase the pH by one unit (which is independent of the previous answer) proved too much for almost all candidates. In part (e) most students could quote and substitute into the ideal gas equation, but converting from \({{\text{m}}^3}\) to \({\text{c}}{{\text{m}}^3}\) posed a problem for most candidates. Quite a number of candidates were however able to calculate the pH of the sulfur dioxide solution and identify a stronger acid.
This was quite a popular question, though generally not well answered. In the first part students again appeared to display a lack of expertise in a practical context with very few able to devise a mixture that would halve the concentration of thiosulfate, whilst keeping other concentrations constant, and answers predicting that this would halve the reaction time were far more commonly encountered than those doubling it. Many candidates did however suggest valid reasons why the reaction vessel should remain unchanged and a significant number of students were able to correctly deduce the rate equation that the mechanism given would predict. Again a lack of ability to interpret experimental data was evident in the fact that it was very rare to find students who realised that a graph of (time)-1 against concentration was required to be able to deduce the reaction order, with almost all simply plotting time-concentration graphs and, as a result, very few could evaluate the mechanism in the light of the experimental data. Part (c) was a fairly standard question on the effect of temperature on reaction rate, hence it was a surprise that students did not score better on it, with many of the oft repeated mistakes (number of collisions rather than collision frequency) again coming to the surface. Again it was probably inability to interpret experimental data that led to only very few students being able to correctly state the initial pH of the mixture (I am certain almost all would have gained the mark if the pH of \({\text{ 0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) HCl had been asked for) and the percentage that would have to be consumed to increase the pH by one unit (which is independent of the previous answer) proved too much for almost all candidates. In part (e) most students could quote and substitute into the ideal gas equation, but converting from \({{\text{m}}^3}\) to \({\text{c}}{{\text{m}}^3}\) posed a problem for most candidates. Quite a number of candidates were however able to calculate the pH of the sulfur dioxide solution and identify a stronger acid.
This was quite a popular question, though generally not well answered. In the first part students again appeared to display a lack of expertise in a practical context with very few able to devise a mixture that would halve the concentration of thiosulfate, whilst keeping other concentrations constant, and answers predicting that this would halve the reaction time were far more commonly encountered than those doubling it. Many candidates did however suggest valid reasons why the reaction vessel should remain unchanged and a significant number of students were able to correctly deduce the rate equation that the mechanism given would predict. Again a lack of ability to interpret experimental data was evident in the fact that it was very rare to find students who realised that a graph of (time)-1 against concentration was required to be able to deduce the reaction order, with almost all simply plotting time-concentration graphs and, as a result, very few could evaluate the mechanism in the light of the experimental data. Part (c) was a fairly standard question on the effect of temperature on reaction rate, hence it was a surprise that students did not score better on it, with many of the oft repeated mistakes (number of collisions rather than collision frequency) again coming to the surface. Again it was probably inability to interpret experimental data that led to only very few students being able to correctly state the initial pH of the mixture (I am certain almost all would have gained the mark if the pH of \({\text{ 0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) HCl had been asked for) and the percentage that would have to be consumed to increase the pH by one unit (which is independent of the previous answer) proved too much for almost all candidates. In part (e) most students could quote and substitute into the ideal gas equation, but converting from \({{\text{m}}^3}\) to \({\text{c}}{{\text{m}}^3}\) posed a problem for most candidates. Quite a number of candidates were however able to calculate the pH of the sulfur dioxide solution and identify a stronger acid.

