| Date | May 2015 | Marks available | 1 | Reference code | 15M.2.hl.TZ2.7 |
| Level | HL | Paper | 2 | Time zone | TZ2 |
| Command term | Define | Question number | 7 | Adapted from | N/A |
Question
When nitrogen gas and hydrogen gas are allowed to react in a closed container the following equilibrium is established.
\[{{\text{N}}_{\text{2}}}{\text{(g)}} + {\text{3}}{{\text{H}}_{\text{2}}}{\text{(g)}} \rightleftharpoons {\text{2N}}{{\text{H}}_{\text{3}}}{\text{(g) }}\Delta H = -92.6{\text{ kJ}}\]
Outline two characteristics of a reversible reaction in a state of dynamic equilibrium.
Predict, with a reason, how each of the following changes affects the position of equilibrium.
The volume of the container is increased.
Ammonia is removed from the equilibrium mixture.
Define the term activation energy, \({E_{\text{a}}}\).
Ammonia is manufactured by the Haber process in which iron is used as a catalyst.
Explain the effect of a catalyst on the rate of reaction.
Typical conditions used in the Haber process are 500 °C and 200 atm, resulting in approximately 15% yield of ammonia.
(i) Explain why a temperature lower than 500 °C is not used.
(ii) Outline why a pressure higher than 200 atm is not often used.
Deduce the equilibrium constant expression, \({K_{\text{c}}}\), for the reaction on page 10.
When 1.00 mol of nitrogen and 3.00 mol of hydrogen were allowed to reach equilibrium in a \({\text{1.00 d}}{{\text{m}}^{\text{3}}}\) container at a temperature of 500 °C and a pressure of 1000 atm, the equilibrium mixture contained 1.46 mol of ammonia.
Calculate the value of \({K_{\text{c}}}\) at 500 °C.
Define the term base according to the Lewis theory.
Define the term weak base according to the Brønsted–Lowry theory.
Deduce the formulas of conjugate acid-base pairs in the reaction below.
\[{\text{C}}{{\text{H}}_{\text{3}}}{\text{N}}{{\text{H}}_{\text{2}}}{\text{(aq)}} + {{\text{H}}_{\text{2}}}{\text{O(l)}} \rightleftharpoons {\text{C}}{{\text{H}}_{\text{3}}}{\text{NH}}_{\text{3}}^ + {\text{(aq)}} + {\text{O}}{{\text{H}}^ - }{\text{(aq)}}\]
Determine the pH of a \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) solution of ammonia, \({\text{N}}{{\text{H}}_{\text{3}}}{\text{(aq)}}\), using tables 2 and 15 of the data booklet.
(i) Sketch the pH titration curve obtained when \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{N}}{{\text{H}}_{\text{3}}}{\text{(aq)}}\) is added to \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{HCl (aq)}}\).

(ii) Identify an indicator from table 16 of the data booklet that could be used for this titration.
Markscheme
rates of forward and reverse reactions are equal / opposing changes occur at equal rates;
the concentrations of all reactants and products remain constant / macroscopic properties remain constant;
closed/isolated system;
Accept “the same” for “equal” in M1 and for “constant” in M2.
The volume of the container is increased:
position of equilibrium shifts to the left/reactants and fewer moles of gas on the right hand side/pressure decreases / OWTTE;
Ammonia is removed from the equilibrium mixture:
position of equilibrium shifts to the right/products and \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) decreases so \({\text{[}}{{\text{N}}_{\text{2}}}{\text{]}}\) and \({\text{[}}{{\text{H}}_{\text{2}}}{\text{]}}\) must also decrease to keep Kc constant
OR
position of equilibrium shifts to the right/products and rate of reverse reaction decreases / OWTTE;
Award [1 max] if both predicted changes are correct.
Do not accept “to increase \([N{H_3}]\)” or reference to LCP without explanation.
minimum energy needed (by reactants/colliding particles) to react/start/initiate a reaction;
Accept “energy difference between reactants and transition state”.
more effective/successful collisions per unit time / greater proportion of collisions effective;
alternative pathway and a lower activation energy
OR
lowers activation energy so that more particles have enough energy to react;
Do not accept just “lowers/reduces the activation energy”.
Accept “provides a surface for reacting/reactants/reaction”.
(i) slower rate / OWTTE;
uneconomic / OWTTE;
(ii) high cost for building/maintaining plant / high energy cost of compressor / OWTTE;
Do not accept “high pressure is expensive” without justification.
Accept high pressure requires high energy.
\(({K_{\text{c}}} = )\frac{{{{{\text{[N}}{{\text{H}}_3}{\text{(g)]}}}^2}}}{{{\text{[}}{{\text{N}}_2}{\text{(g)]}} \times {{{\text{[}}{{\text{H}}_2}{\text{(g)]}}}^3}}}\);
Ignore state symbols.
Concentrations must be represented by square brackets.
moles at equilibrium: nitrogen 0.27, hydrogen 0.81 / concentrations at equilibrium: nitrogen \({\text{0.27 (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\), hydrogen \({\text{0.81 (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) (and ammonia \({\text{1.46 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\));
\({K_{\text{c}}} = 15\);
Actual calculation gives \({K_{\text{c}}}{\text{ = }}14{\text{.}}86\).
Award [2] for correct final answer.
Award [1 max] if \({K_{\text{c}}}\left( { = \frac{{{{1.46}^2}}}{{{3^3} \times 1}}} \right) = 0.079\)
electron pair donor;
Accept lone pair donor.
proton acceptor and partially/slightly ionized;
Accept “proton acceptor and partially/slightly dissociated”.
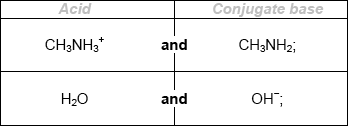
Award [1 max] for two correct acids OR two correct conjugate bases.
\({K_{\text{b}}} = \frac{{{\text{[NH}}_4^ + {\text{][O}}{{\text{H}}^ - }{\text{]}}}}{{{\text{[N}}{{\text{H}}_3}{\text{]}}}} = 1.8 \times {10^{ - 5}}/{10^{ - 4.75}}\);
\({\text{[NH}}_4^ + {\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\) and \({\text{[N}}{{\text{H}}_3}{\text{]}} \approx 1.00 \times {10^{ - 1}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
\({\text{[O}}{{\text{H}}^ - }{\text{]}} = (\sqrt {1.8 \times {{10}^{ - 6}}} = )1.3 \times {10^{ - 3}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}/{\text{pOH}} = 2.89\);
\({\text{pH}} = (14.0 - 2.89 = )11.1\);
Award [4] for correct final answer.
(i) 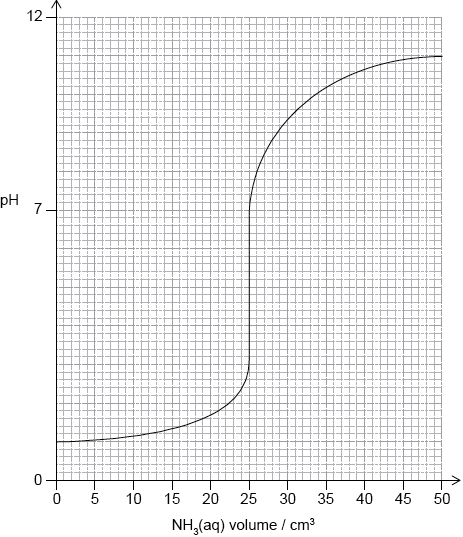
For volume \( = 0:{\text{ pH}} = 1\);
vertical jump should be positioned in volume range \({\text{24 c}}{{\text{m}}^{\text{3}}}\) to \({\text{26 c}}{{\text{m}}^{\text{3}}}\) and include pH range between 3 to 6;
For volume = 50: pH between 8 to 11;
(ii) methyl orange / bromophenol blue / bromocresol green / methyl red;
Examiners report
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.

