| Date | May 2013 | Marks available | 1 | Reference code | 13M.2.sl.TZ2.2 |
| Level | SL | Paper | 2 | Time zone | TZ2 |
| Command term | Define | Question number | 2 | Adapted from | N/A |
Question
The standard enthalpy change of three combustion reactions are given below.
\[\begin{array}{*{20}{l}} {{{\text{H}}_2}{\text{(g)}} + \frac{1}{2}{{\text{O}}_2}{\text{(g)}} \to {{\text{H}}_2}{\text{O(l)}}}&{\Delta H = - 286{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}} \\ {{{\text{C}}_3}{{\text{H}}_8}{\text{(g)}} + {\text{5}}{{\text{O}}_2}{\text{(g)}} \to {\text{3C}}{{\text{O}}_2}{\text{(g)}} + {\text{4}}{{\text{H}}_2}{\text{O(l)}}}&{\Delta H = - 2219{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}} \\ {{\text{C(s)}} + {{\text{O}}_2}{\text{(g)}} \to {\text{C}}{{\text{O}}_2}{\text{(g)}}}&{\Delta H = - 394{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}} \end{array}\]
Determine the change in enthalpy, \(\Delta H\), in \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\), for the formation of propane in the following reaction.
\({\text{3C(s)}} + {\text{4}}{{\text{H}}_2}{\text{(g)}} \to {{\text{C}}_3}{{\text{H}}_8}{\text{(g)}}\)
A catalyst provides an alternative pathway for a reaction, lowering the activation energy, \({E_{\text{a}}}\). Define the term activation energy, \({E_{\text{a}}}\).
Sketch two Maxwell–Boltzmann energy distribution curves for a fixed amount of gas at two different temperatures, \({T_{\text{1}}}\) and \({T_2}{\text{ }}({T_2} > {T_1})\) and label both axes.

Markscheme
\({\text{4}}{{\text{H}}_{\text{2}}}{\text{O(l)}} + {\text{3C}}{{\text{O}}_2}{\text{(g)}} \to {{\text{C}}_3}{{\text{H}}_8}{\text{(g)}} + {\text{5}}{{\text{O}}_2}{\text{(g)}}\) \(\Delta H = + {\text{2219 (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
\({\text{4}}{{\text{H}}_2}{\text{(g)}} + {\text{2}}{{\text{O}}_2}{\text{(g)}} \to {\text{4}}{{\text{H}}_2}{\text{O(l)}}\): \(\Delta H = \left( {{\text{(}} - {\text{286)(4)}} = } \right){\text{ }} - {\text{1144 (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
\({\text{3C(s)}} + {\text{3}}{{\text{O}}_2}{\text{(g)}} \to {\text{3C}}{{\text{O}}_2}{\text{(g)}}\): \(\Delta H = \left( {{\text{(}} - {\text{394)(3)}} = } \right){\text{ }} - {\text{1182 (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
\(\Delta H = \left( {{\text{(}} - {\text{286)(4)}} + {\text{(}} - {\text{394)(3)}} + {\text{(}} + {\text{2219)}} = } \right){\text{ }} - {\text{107 (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
Award [4] for correct final answer.
minimum energy needed (by reactants/colliding particles) to react/start/initiate a reaction / for a successful collision;
Allow energy difference between reactants and transition state.
x-axis label: (kinetic) energy/(K)E and y-axis label: fraction of molecules/particles / probability density;
Allow velocity/speed for x-axis.
Allow frequency / number of molecules/particles or (kinetic) energy distribution for y-axis.
correct shape of a Maxwell–Boltzmann energy distribution curve;
Do not award mark if curve is symmetric, does not start at zero or if it crosses x-axis.
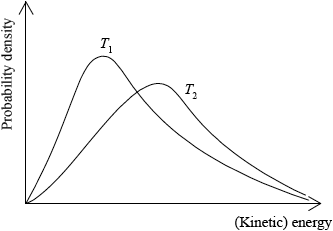
two curves represented with second curve for \({T_2} > {T_1}\) to right of first curve, lower
peak than first curve and after the curves cross \({T_2}\) curve needs to be above \({T_1}\) curve;
Examiners report
In contrast, question 2 a) which involved Hess’s Law calculation, was answered correctly by candidates of all capabilities.
The definition of activation energy in part b) was reasonably well answered, with some candidates losing marks for omitting the word minimum from their response. However, it is disappointing that even very good candidates sometimes fail to score marks for definitions.
Several candidates sketched very clear, correct Maxwell-Boltzmann curves in part c). Most scored at least 1 mark for this question. Some did not know what labels to put on the axes. Some did not realise that the area under the curves represents the total number of particles so as temperature increases the peak of the curve shifts to the right and is lower than the peak at the lower temperature.

