| Date | November 2014 | Marks available | 3 | Reference code | 14N.2.hl.TZ0.11 |
| Level | HL | Paper | 2 | Time zone | TZ0 |
| Command term | Explain and Label | Question number | 11 | Adapted from | N/A |
Question
Hydrogen peroxide decomposes according to the equation below.
\({\text{2}}{{\text{H}}_{\text{2}}}{{\text{O}}_{\text{2}}}{\text{(aq)}} \to {\text{2}}{{\text{H}}_{\text{2}}}{\text{O(l)}} + {{\text{O}}_{\text{2}}}{\text{(g)}}\)
The rate of the decomposition can be monitored by measuring the volume of oxygen gas released. The graph shows the results obtained when a solution of hydrogen peroxide decomposed in the presence of a CuO catalyst.
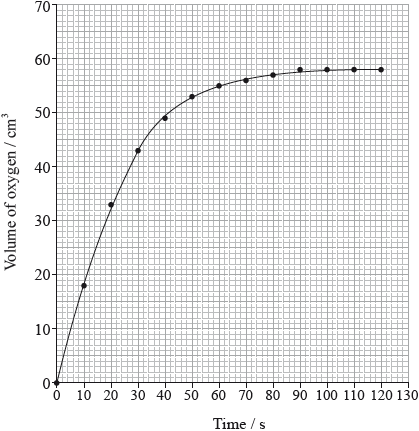
Outline how the initial rate of reaction can be found from the graph.
Explain how and why the rate of reaction changes with time.
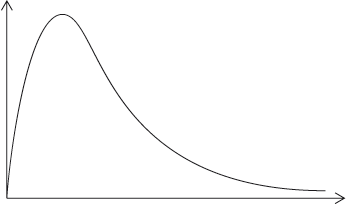
A Maxwell-Boltzmann energy distribution curve is drawn below. Label both axes and explain, by annotating the graph, how catalysts increase the rate of reaction.
(i) In some reactions, increasing the concentration of a reactant does not increase the rate of reaction. Describe how this may occur.
(ii) Consider the reaction
\[{\text{2A}} + {\text{B}} \to {\text{C}} + {\text{D}}\]
The reaction is first order with respect to A, and zero order with respect to B. Deduce the rate expression for this reaction.
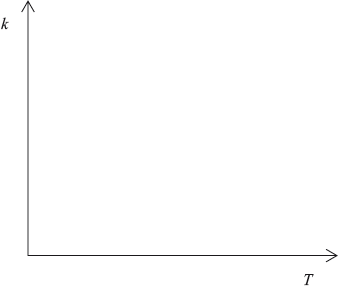
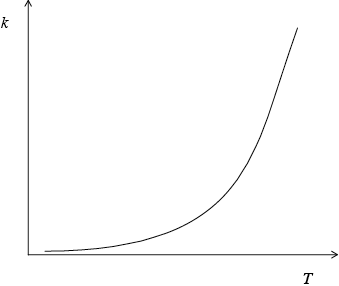
Sketch a graph of rate constant \((k)\) versus temperature.
Hydrochloric acid neutralizes sodium hydroxide, forming sodium chloride and water.
\({\text{NaOH(aq)}} + {\text{HCl(aq)}} \to {\text{NaCl(aq)}} + {{\text{H}}_{\text{2}}}{\text{O(l)}}\) \(\Delta {H^\Theta } = - 57.9{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\)
(i) Define standard enthalpy change of reaction, \(\Delta {H^\Theta }\).
(ii) Determine the amount of energy released, in kJ, when \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{1.00 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sodium hydroxide solution reacts with \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{1.00 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) hydrochloric acid solution.
(iii) In an experiment, 2.50 g of solid sodium hydroxide was dissolved in \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of water. The temperature rose by 13.3 °C. Calculate the standard enthalpy change, in \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\), for dissolving one mole of solid sodium hydroxide in water.
\[{\text{NaOH(s)}} \to {\text{NaOH(aq)}}\]
(iv) Using relevant data from previous question parts, determine \(\Delta {H^\Theta }\), in \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\), for the reaction of solid sodium hydroxide with hydrochloric acid.
\[{\text{NaOH(s)}} + {\text{HCl(aq)}} \to {\text{NaCl(aq)}} + {{\text{H}}_{\text{2}}}{\text{O(l)}}\]
(i) Zinc is found in the d-block of the periodic table. Explain why it is not considered a transition metal.
(ii) Explain why \({\text{F}}{{\text{e}}^{3 + }}\) is a more stable ion than \({\text{F}}{{\text{e}}^{2 + }}\) by reference to their electron configurations.
Markscheme
(draw a) tangent to the curve at origin/time = 0/start of reaction;
(calculate) the gradient/slope (of the tangent);
rate decreases (with time);
concentration/number of (reactant) molecules per unit volume decreases (with time);
Do not accept “number of molecules decreases” or “amount of reactant decreases”.
collisions (between reactant molecules/reactant and catalyst) become less frequent;
Do not accept “fewer collisions” without reference to frequency (eg, no. collisions per second).
y-axis: probability / fraction of molecules/particles / probability density
Allow “number of particles/molecules” on y-axis.
and
x-axis: (kinetic) energy;
Accept “speed/velocity” on x-axis.
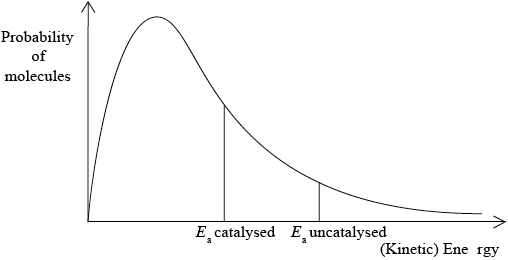
correct relative position of \({E_{\text{a}}}\) catalysed and \({E_{\text{a}}}\) uncatalysed;
more/greater proportion of molecules/collisions have the lower/required/catalysed \({E_{\text{a}}}\) (and can react upon collision);
M3 can be scored by stating or shading and annotating the graph.
Accept “a greater number/proportion of successful collisions as catalyst reduces \({E_a}\)”.
(i) reactant not involved in (or before) the slowest/rate-determining step/RDS;
reactant is in (large) excess;
(ii) \({\text{(rate}} = {\text{) }}k{\text{[A]}}\);
Accept rate = k[A]1[B]0.
curve with a positive slope curving upwards;
Do not penalize if curve passes through the origin.
(i) heat transferred/absorbed/released/enthalpy/potential energy change when 1 mol/molar amounts of reactant(s) react (to form products) / OWTTE;
under standard conditions / at a pressure 100 kPa/101.3 kPa/1 atm and temperature 298 K/25 °C;
Award [2] for difference between standard enthalpies of products and standard enthalpies of reactants / \({H^\Theta }\) (products) – \({H^\Theta }\) (reactants).
Award [2] for difference between standard enthalpies of formation of products and standard enthalpies of formation of reactants / \(\Sigma \Delta H_f^\Theta \) (products) – \(\Sigma \Delta H_f^\Theta \) (reactants).
(ii) \((1.00 \times 0.0500 = ){\text{ }}0.0500{\text{ (mol)}}\);
\((0.0500 \times 57.9 = ){\text{ }}2.90{\text{ (kJ)}}\);
Ignore any negative sign.
Award [2] for correct final answer.
Award [1 max] for 2900 J.
(iii) \(\left( {\frac{{2.50}}{{40.00}} = } \right){\text{ }}0.0625{\text{ (mol NaOH)}}\);
\(0.0500 \times 4.18 \times 13.3 = 2.78{\text{ (kJ)}}/50.0 \times 4.18 \times 13.3 = 2780{\text{ (J)}}\);
\(\left( {\frac{{2.78}}{{0.0625}}} \right) = - 44.5{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}})\);
Award [3] for correct final answer.
Negative sign is necessary for M3.
Award M2 and M3 if is used to obtain an enthalpy change of –46.7 (kJ mol–1).
(iv) \( - 44.5 - 57.9\) / correct Hess’s Law cycle (as below) / correct manipulation of equations;
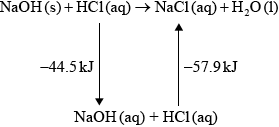
\( - 102.4{\text{ kJ}}\);
Award [2] for correct final answer.
(i) zinc (only) forms the ion \({\text{Z}}{{\text{n}}^{2 + }}\) / has the oxidation state \( + 2\);
Allow forms only one ion / has only one oxidation state.
has full d-subshell/orbitals / does not have a partially filled d-subshell/orbitals (needed to exhibit transition metal properties);
(ii) \({\text{F}}{{\text{e}}^{2 + }}{\text{: 1}}{{\text{s}}^{\text{2}}}{\text{2}}{{\text{s}}^{\text{2}}}{\text{2}}{{\text{p}}^{\text{6}}}{\text{3}}{{\text{s}}^{\text{2}}}{\text{3}}{{\text{p}}^{\text{6}}}{\text{3}}{{\text{d}}^{\text{6}}}/{\text{[Ar] 3}}{{\text{d}}^{\text{6}}}\) and \({\text{F}}{{\text{e}}^{3 + }}{\text{: 1}}{{\text{s}}^{\text{2}}}{\text{2}}{{\text{s}}^{\text{2}}}{\text{2}}{{\text{p}}^{\text{6}}}{\text{3}}{{\text{s}}^{\text{2}}}{\text{3}}{{\text{p}}^{\text{6}}}{\text{3}}{{\text{d}}^{\text{5}}}/{\text{[Ar] 3}}{{\text{d}}^{\text{5}}}\);
half-full sub-level/3d5 has extra stability;
less repulsion between electrons / electrons singly occupy orbitals / electrons do not have to pair with other electrons;
Accept converse points for Fe2+.
Examiners report
Most candidates related the rate of reaction to the gradient of the curve, but only a few suggested drawing a tangent at \(t = 0\).
Answers were often disappointing and only a few candidates gained full marks.
Candidates often talked about the number of reactant molecules decreasing but neglected to relate this to a lower concentration. Also some candidates still fail to highlight frequency rather than the number of collisions.
Well answered by more than half of the candidates. The labelling of the axes was a challenge for some candidates. The annotation of the diagram with the energy of activation with and without a catalyst was mostly correct, though some weaker students confused it with the effect of temperature and constructed a second curve. Some candidates could not offer an explanation for the third mark.
(i) Only a few candidates scored this mark. Many candidates stated that a reactant concentration having no effect indicated that the reaction that was zero order in that species, rather than describing the underlying mechanistic reason for the zero order dependence.
(ii) More than half of the candidates could construct a correct rate expression from information about the order of the reactants.
A number of candidates gave a linear relationship, rather than an exponential one, between reaction rate and temperature.
(i) Defining the standard enthalpy change of reaction was not well answered.
(ii) More than half of the candidates calculated the amount of energy released correctly.
(iii) Half of the candidates were able to gain the three marks. Many candidates lost the third mark for not quoting the negative sign for the enthalpy change. Quite a few candidates used a wrong value for the mass of water.
(iv) Many good answers. A Hess’s Law cycle wasn’t often seen. Quite a few candidates scored through ECF from (iii).
(i) Most candidates knew that zinc has a full 3d sub-shell but almost all missed out on the second mark about only having one possible oxidation state in its compounds.
(ii) This was a challenging question for many candidates. A large number of candidates did not give the correct electron configurations for the ions, and only few mentioned the stability of the half-full d-sub-shell. Very few scored the third mark.

