| Date | November 2012 | Marks available | 1 | Reference code | 12N.2.hl.TZ0.6 |
| Level | HL | Paper | 2 | Time zone | TZ0 |
| Command term | Describe | Question number | 6 | Adapted from | N/A |
Question
Chemical kinetics involves an understanding of how the molecular world changes with time.
A catalyst provides an alternative pathway for a reaction, lowering the activation energy, \({E_{\text{a}}}\).
Sketch graphical representations of the following reactions, for X \( \to \) products.
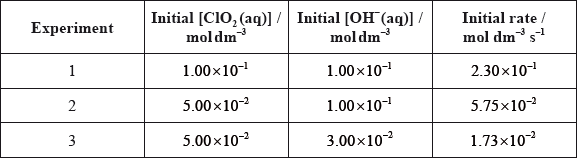
For the reaction below, consider the following experimental data.
\[{\text{2Cl}}{{\text{O}}_2}{\text{(aq)}} + {\text{2O}}{{\text{H}}^ - }{\text{(aq)}} \to {\text{ClO}}_3^ - {\text{(aq)}} + {\text{ClO}}_2^ - {\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}}\]
Another reaction involving \({\rm{O}}{{\rm{H}}^ - }\) (aq) is the base hydrolysis reaction of an ester.
\[{\text{C}}{{\text{H}}_3}{\text{COOC}}{{\text{H}}_2}{\text{CH(aq)}} + {\text{O}}{{\text{H}}^ - }{\text{(aq)}} \to {\text{C}}{{\text{H}}_3}{\text{CO}}{{\text{O}}^ - }{\text{(aq)}} + {\text{C}}{{\text{H}}_3}{\text{C}}{{\text{H}}_2}{\text{OH(aq)}}\]
A two-step mechanism has been proposed for the following reaction.
\[\begin{array}{*{20}{l}} {{\text{Step 1:}}}&{{\text{Cl}}{{\text{O}}^ - }{\text{(aq)}} + {\text{Cl}}{{\text{O}}^ - }{\text{(aq)}} \to {\text{ClO}}_2^ - {\text{(aq)}} + {\text{C}}{{\text{l}}^ - }{\text{(aq)}}} \\ {{\text{Step 2:}}}&{{\text{ClO}}_2^ - {\text{(aq)}} + {\text{Cl}}{{\text{O}}^ - }{\text{(aq)}} \to {\text{ClO}}_3^ - {\text{(aq)}} + {\text{C}}{{\text{l}}^ - }{\text{(aq)}}} \end{array}\]
(i) Define the term rate of reaction.
(ii) Temperature and the addition of a catalyst are two factors that can affect the rate of a reaction. State two other factors.
(iii) In the reaction represented below, state one method that can be used to measure the rate of the reaction.
\[{\text{ClO}}_3^ - {\text{(aq)}} + {\text{5C}}{{\text{l}}^ - }{\text{(aq)}} + {\text{6}}{{\text{H}}^ + }{\text{(aq)}} \to {\text{3C}}{{\text{l}}_2}{\text{(aq)}} + {\text{3}}{{\text{H}}_2}{\text{O(l)}}\]
(i) Define the term activation energy, \({E_{\text{a}}}\).
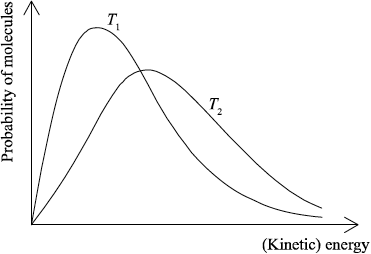
(ii) Sketch the two Maxwell–Boltzmann energy distribution curves for a fixed amount of gas at two different temperatures, \({T_1}\) and \({T_2}{\text{ }}({T_2} > {T_1})\). Label both axes.

(i) Concentration of reactant X against time for a zero-order reaction.
(ii) Rate of reaction against concentration of reactant X for a zero-order reaction.
(iii) Rate of reaction against concentration of reactant X for a first-order reaction.
(i) Deduce the rate expression.
(ii) Determine the rate constant, \(k\), and state its units, using the data from Experiment 2.
(iii) Calculate the rate, in \({\text{mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{{\text{s}}^{ - 1}}\), when \({\text{[Cl}}{{\text{O}}_2}{\text{(aq)]}} = 1.50 \times {10^{ - 2}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) and \({\text{[O}}{{\text{H}}^ - }{\text{(aq)]}} = 2.35 \times {10^{ - 2}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\).
Apply IUPAC rules to name the ester, CH3COOCH2CH3(aq).
Describe qualitatively the relationship between the rate constant, k, and temperature, T.
The rate of this reaction was measured at different temperatures and the following data were recorded.
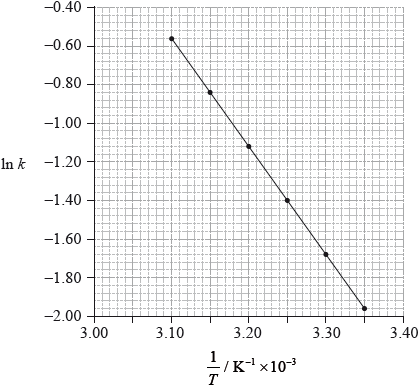
Using data from the graph, determine the activation energy, \({E_{\text{a}}}\), correct to three significant figures and state its units.
Deduce the overall equation for the reaction.
Deduce the rate expression for each step.
Step 1:
Step 2:
Markscheme
(i) change in concentration of reactant/product with time / rate of change of concentration;
Increase can be used instead of change for product or decrease can be used instead of change for reactant.
Allow mass/amount/volume instead of concentration.
Do not accept substance.
(ii) concentration;
particle size / surface area;
light;
pressure;
Allow pH.
(iii) (measuring electrical) conductivity / (measuring) pH;
Accept other suitable method.
(i) minimum/least/smallest energy needed (by reactants/colliding particles) to react/start/initiate a reaction;
Allow energy difference between reactants and transition state.
Minimum/least/smallest required for the mark.
(ii) x-axis label: (kinetic) energy/(K)E and y-axis label: probability/fraction of molecules/particles / probability density;
Allow number of molecules/particles for y-axis.
correct shape of a typical Maxwell–Boltzmann energy distribution curve;
Do not award mark if curve is symmetric, does not start at zero or if it crosses x-axis.
two curves represented with second curve for \({T_2} > {T_1}\) to right of first curve, peak maximum lower than first curve and after the curves cross going to the right, \({T_2}\) curve needs to be above \({T_1}\) curve as illustrated;
M2 and M3 can be scored independently.
(i) 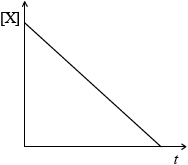 ;
;
(ii) 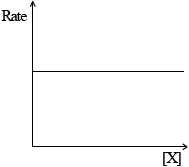 ;
;
(iii) 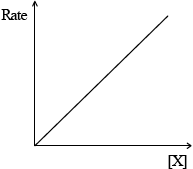 ;
;
(i) second order in \({\text{Cl}}{{\text{O}}_2}\) and first order in \({\text{O}}{{\text{H}}^ - }\);
rate \( = k{{\text{[Cl}}{{\text{O}}_{\text{2}}}{\text{]}}^2}{\text{[O}}{{\text{H}}^ - }{\text{]}}\);
Award [2] for correct final answer.
(ii) \(k = 2.30 \times {10^2}/230\);
\({\text{mo}}{{\text{l}}^{ - 2}}{\text{d}}{{\text{m}}^6}{{\text{s}}^{ - 1}}\);
(iii) \(1.22 \times {10^{ - 3}}/0.00122{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{{\text{s}}^{ - 1}}{\text{)}}\);
ethyl ethanoate;
Do not allow ethyl acetate.
as temperature/T increases, (value of) rate constant/k increases (exponentially);
Do not allow answers involving ln k from the Arrhenius equation.
Do not allow T directly proportional to k.
slope \( = - 5.6 \times {10^3}/ - 5600{\text{ (K)}}\);
\({E_{\text{a}}} = - {\text{slope}} \times {\text{R}}/{\text{slope}} = - {E_{\text{a}}}/R\);
\({E_{\text{a}}}{\text{(}} = 5.60 \times {10^3}{\text{ }}K \times 8.31{\text{ J}}\,{{\text{K}}^{ - 1}}{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}} = 4.65 \times {10^4}{\text{ (J}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}/46.5{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
Accept answers in range 4.60 \( \times \) 104 J\(\,\)mol\(^{ - 1}\) to 4.67 \( \times \) \({10^4}\) (J mol \(^{ - 1}\)).
\({\text{J}}\,{\text{mo}}{{\text{l}}^{ - 1}}/{\text{kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\);
Accept J or kJ.
Unit mark can be scored independently but correct \({E_a}\) values with incorrect units scores only [3 max] (for example 46.5 J mol \(^{ - 1}\)).
Award [4] for correct final answer.
\({\text{3Cl}}{{\text{O}}^ - }{\text{(aq)}} \to {\text{ClO}}_3^ - {\text{(aq)}} + {\text{2C}}{{\text{l}}^ - }{\text{(aq)}}\);
Ignore state symbols.
Step 1: rate \( = k{{\text{[Cl}}{{\text{O}}^ - }{\text{]}}^{\text{2}}}\);
Step 2: rate \( = k{\text{[ClO}}_2^ - {\text{][Cl}}{{\text{O}}^ - }{\text{]}}\);
Penalize missing k once only.
Examiners report
This was the most popular question in Section B of the paper. Part (a) was very well answered.
In (b) (i), some candidates failed to mention minimum/least/smallest energy in the definition of activation energy. In part (ii), again candidates often dropped easy marks here for poor representations of the Maxwell-Boltzmann energy distribution curves. In some cases the curves were drawn symmetrically, which was incorrect. In addition, incorrect labels were often given for the x- and y-axes. Some candidates mixed these curves up with enthalpy level diagrams. It was nice to see more candidates giving a more precise label for the y-axis as probability/fraction of molecules rather than just number of molecules. The latter was allowed but is less precise (although does tend to be used in many IB textbooks).
Part (c) however was very well answered.
In part (d), many candidates also scored highly though the units of k in (ii) did cause a problem for some candidates.
In (e) (i), the most common mistake was candidates stating ethyl methanoate instead of ethyl ethanoate.
In part (ii), a number of candidates stated incorrectly that T is directly proportional to k, which is incorrect. Proportionality is a concept embedded in AS 11.3.1 in Topic 11, and may be worth some further discussion in the light of the Arrhenius Equation.
The most difficult part of Q6 however involved (e) (iii). Very few candidates scored full marks here and simply did not know how to manipulate the equation to get the activation energy. Others even gave incorrect units.
One respondent stated that part (f) (ii) would be difficult for candidates. (f) certainly did prove challenging and the rate expression for step two was often given incorrectly. This question became a good discriminating question in Section B. However the better students did manage to score all three marks in part (f).
One respondent stated that part (f) (ii) would be difficult for candidates. (f) certainly did prove challenging and the rate expression for step two was often given incorrectly. This question became a good discriminating question in Section B. However the better students did manage to score all three marks in part (f).

