| Date | May 2017 | Marks available | 2 | Reference code | 17M.1.sl.TZ2.6 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 6 | Adapted from | N/A |
Question
For a study, a researcher collected 200 leaves from oak trees. After measuring the lengths of the leaves, in cm, she produced the following cumulative frequency graph.
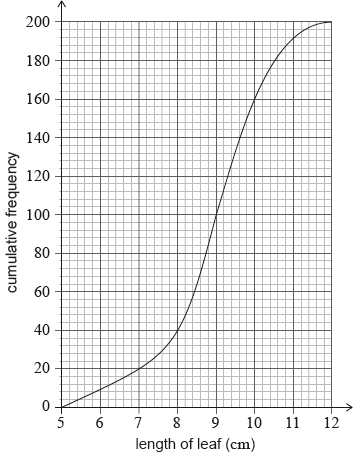
The researcher finds that 10% of the leaves have a length greater than \(k\) cm.
Write down the median length of these leaves.
Write down the number of leaves with a length less than or equal to 8 cm.
Use the graph to find the value of \(k\).
Before measuring, the researcher estimated \(k\) to be approximately 9.5 cm. Find the percentage error in her estimate.
Markscheme
9 (cm) (A1) (C1)
[1 mark]
40 (leaves) (A1) (C1)
[1 mark]
\((200 \times 0.90 = ){\text{ }}180\) or equivalent (M1)
Note: Award (M1) for a horizontal line drawn through the cumulative frequency value of 180 and meeting the curve (or the corresponding vertical line from 10.5 cm).
\((k = ){\text{ }}10.5{\text{ (cm)}}\) (A1) (C2)
Note: Accept an error of ±0.1.
[2 marks]
\(\left| {\frac{{9.5 - 10.5}}{{10.5}}} \right| \times 100\% \) (M1)
Notes: Award (M1) for their correct substitution into the percentage error formula.
\({\text{9.52 (% ) }}\left( {{\text{9.52380}} \ldots {\text{ (% )}}} \right)\) (A1)(ft) (C2)
Notes: Follow through from their answer to part (c)(i).
Award (A1)(A0) for an answer of \( - 9.52\) with or without working.
[2 marks]
Examiners report
Syllabus sections
- 10M.1.sl.TZ2.10a: Find the interest Astrid has earned during the five years of her investment. Give your answer...
- 13M.2.sl.TZ1.5g: The cost of one square metre of glass used to construct the greenhouse is 4.80...
- SPM.2.sl.TZ0.1e: Sam estimated the value of the mean of the measured lengths to be \(43{\text{ cm}}\). Find...
- 08N.1.sl.TZ0.5c: On her return to Singapore, Kwai Fan has \(2500\) Indian rupees left from her trip. She...
- 08M.1.sl.TZ1.1c: Calculate the percentage error when the answer to part (a) is written correct to 2...
- 15M.2.sl.TZ2.2e: Temi sells her perfume bottles in a craft fair for 325 ZAR each. Dominique from France buys...
- 16N.1.sl.TZ0.1c: Write your answer to part (b)(ii) in the form \(a \times {10^k}\), where...
- 16N.2.sl.TZ0.3f: Write down the length of MD correct to five significant figures.
- 11M.1.sl.TZ1.1b: Barry first writes \(x\) , \(y\) and \(z\) correct to one significant figure and then uses...
- 11M.1.sl.TZ1.5b: Calculate the distance travelled by the satellite in one orbit of the Earth. Give your answer...
- 09M.1.sl.TZ1.10b: Nadia makes an accurate drawing of triangle ABC. She measures angle BAC and finds it to be...
- SPM.1.sl.TZ0.11a: Find the value of the investment after 3 years.
- SPM.2.sl.TZ0.3e: The selling price, in US dollars (USD), of each size is shown in the table below.The...
- 07N.2.sl.TZ0.3ii.a: Calculate correct to 2 decimal places the amount of euros he receives.
- 08N.1.sl.TZ0.1b: Write down the answer to part (a) correct to three decimal places.
- 08M.2.sl.TZ1.1d: Using your graphical display calculator write down the coordinates of one of the points of...
- 16N.2.sl.TZ0.3b: Find the coordinates of M.
- 16N.1.sl.TZ0.8d: Find the percentage error.
- 16M.1.sl.TZ1.6c: Anisha visits the amphitheatre. She estimates that the amphitheatre has \(6500\)...
- 17M.1.sl.TZ2.6b: Write down the number of leaves with a length less than or equal to 8 cm.
- 17N.2.sl.TZ0.3d.ii: Find the percentage error in Abdallah’s estimate.
- 17N.2.sl.TZ0.3a: Show that \({\text{BD}} = 93{\text{ m}}\) correct to the nearest metre.
- 18M.1.sl.TZ1.1c: Write down your answer to part (b) in the form a × 10k where 1 ≤ a < 10,...
- 09N.1.sl.TZ0.8a: Find the exchange rate between GBP and EUR in the form 1 GBP = k EUR, where k is a constant....
- 09N.1.sl.TZ0.15b: Mr Black invested 5000 CHF in Bank B at a nominal annual interest rate of 3.6 %, compounded...
- 11M.1.sl.TZ2.6c: A local newspaper claims that the mean number of goals scored per match is two. Calculate the...
- 13M.1.sl.TZ2.15a: Calculate the total amount of interest Marcus would earn, in AUD, over the three years. Give...
- 07M.2.sl.TZ0.4ii.d: Explain why the sum of the first 1000 terms of G2 will give the same answer as the sum of the...
- 08N.1.sl.TZ0.1c: Write down the answer to part (a) correct to three significant figures.
- 08N.1.sl.TZ0.5a: Kwai Fan changes \({\text{S\$ }}500\) to Indian rupees. Calculate the number of Indian...
- 08M.1.sl.TZ1.1b: Write the answer to part (a) correct to 2 significant figures.
- 14M.1.sl.TZ1.12c: Ludmila estimates that she will have to repay \({\text{360}}\,{\text{000}}\) BRL at the end...
- 15M.1.sl.TZ1.5b: The volume of the Moon is \(2.1958 \times {10^{10}}\;{\text{k}}{{\text{m}}^3}\). Calculate...
- 16N.1.sl.TZ0.1a: Calculate the value of \(p\). Write down your full calculator display.
- 16M.1.sl.TZ1.6b: There are \(20\) rows in the amphitheatre. Find the total number of seats in the amphitheatre.
- 16M.1.sl.TZ1.6a: One of the locations in the \(2016\) Olympic Games is an amphitheatre. The number of seats in...
- 17M.2.sl.TZ1.1b.i: For the data from these seven species calculate \(r\), the Pearson’s product–moment...
- 17M.2.sl.TZ1.1e: Find the percentage error in your estimate in part (d).
- 17M.2.sl.TZ1.1f: State whether it is valid to use the regression line to estimate the average weight of the...
- 10M.1.sl.TZ1.5b: Write down your answer to (a) correct to the nearest integer.
- 10M.2.sl.TZ2.2e: Using your graph, estimate the time when Alex and Kris pass the 85 km distance marker. Give...
- 09N.1.sl.TZ0.3b: Helen’s estimate of the area of the rectangle is \(1\,600\,000{\text{...
- 09N.1.sl.TZ0.8b: Isabella changes 400 USD into Euros and is charged 2 % commission. Calculate how many Euros...
- 09M.1.sl.TZ2.1b: Find the area of the rectangle, giving your answer correct to the nearest thousand square...
- 07M.1.sl.TZ0.1b: Calculate \(\sqrt {{{3.87}^5} - {{8.73}^{ - 0.5}}} \), giving your answer (i) correct to the...
- 07M.2.sl.TZ0.2i.a: Calculate the volume of the cylinder in cm3. Give your answer correct to two decimal places.
- 08M.1.sl.TZ2.11a: Minbin has \(1250\) Japanese Yen which she wishes to exchange for Chinese Yuan. Calculate...
- 08M.1.sl.TZ2.11b: Rupert has \(855\) Canadian Dollars which he wishes to exchange for Japanese Yen. Calculate...
- 15M.1.sl.TZ1.1c: Pyotr estimates the value of \(T\) to be \(0.002\). Calculate the percentage error in...
- 15M.1.sl.TZ1.1b: Give your answer to \(T\) correct to (i) two significant figures; (ii) three...
- 15M.2.sl.TZ2.2d: Temi covers the perfume bottles with a paint that costs 3 South African rand (ZAR) per...
- 14N.2.sl.TZ0.1h: A cricket makes 20 chirps in 15 seconds. For this chirp rate (i) calculate an estimate...
- 16N.2.sl.TZ0.3a: Show that A lies on \({L_1}\).
- 17M.2.sl.TZ1.1b.ii: For the data from these seven species describe the correlation between the average body...
- 17M.2.sl.TZ1.1c: Write down the equation of the regression line \(y\) on \(x\), in the form \(y = mx + c\).
- 18M.1.sl.TZ1.1a: Based on the owner’s claim, calculate the total attendance for the games at Peterson United’s...
- 18M.2.sl.TZ2.5a.iii: Use Giovanni's diagram to find the length of BX, the horizontal displacement of the Tower.
- 18M.2.sl.TZ2.5b: Find the percentage error on Giovanni’s diagram.
- 10M.1.sl.TZ2.1c: José estimates the angle between the horizontal and the top of the cliff as 28.3° and uses it...
- 10N.1.sl.TZ0.3c: The actual number of cubes in the box is 350. Find the percentage error in Joaquin’s...
- 12N.1.sl.TZ0.3c: Marian calculates the mean length and finds it to be 105 cm. Calculate the percentage error...
- 12M.2.sl.TZ1.1f: The population of Beartown is 120 000. The local radio station claimed that 34 000 of the...
- 11M.2.sl.TZ1.5b: The fence costs \(17\) USD per metre to build. Calculate the cost of building the fence....
- SPM.1.sl.TZ0.11b: Find the difference in the final value of the investment if the interest was compounded...
- 15M.1.sl.TZ2.1b: Write down your answer to part (a) correct to three significant figures.
- 16N.2.sl.TZ0.3e: Find the coordinates of D.
- 16N.1.sl.TZ0.8c: Find the value of \(x\) and the value of \(y\).
- 17M.2.sl.TZ1.1a: Find the range of the average body weights for these seven species of mammal.
- 17M.1.sl.TZ2.6a: Write down the median length of these leaves.
- 17N.2.sl.TZ0.3d.i: Calculate Abdallah’s estimate for the area.
- 18M.2.sl.TZ2.5a.i: Use Giovanni’s diagram to show that angle ABC, the angle at which the Tower is leaning...
- 10M.1.sl.TZ1.1b: Jim estimates the dimensions of the container as 15 m, 2 m and 3 m and uses these to estimate...
- 10M.1.sl.TZ1.5a: Calculate the volume of the sphere. Give your answer correct to two decimal places.
- 10M.1.sl.TZ2.12c: Determine the length of time it would take for 150 teenagers to have heard the rumour. Give...
- 11N.1.sl.TZ0.1b.iii: Write your answer to part (a) in the form \(a \times {10^k}\), where 1 ≤ a < 10,...
- 12M.1.sl.TZ1.3b: Give your answer to part (a) in years. (Assume 1 year = 365 days)
- 13M.1.sl.TZ1.11b: Calculate the number of American dollars (USD) Neung takes home. Give your answer correct to...
- 07M.1.sl.TZ0.1a: (i) Find the mean of the contractor’s measurements. (ii) Calculate the percentage error...
- 07N.1.sl.TZ0.1c: Juan estimates the length of a carpet to be 12 metres and the width to be 8 metres. He then...
- 07N.2.sl.TZ0.3ii.b: He buys 1 kilogram of Belgian chocolates at 1.35 euros per 100 g. Calculate the cost of his...
- 14M.2.sl.TZ2.2a: Using ‘distance = speed \( \times \) time’, show that the distance...
- 13N.2.sl.TZ0.1h: The actual price of the return ticket is \(\$80\). Using your answer to part (f), calculate...
- 14M.1.sl.TZ1.1a: Calculate the value of \(p\) when \(x = 45^\circ \), \(y = 8192\) and \(z = 64\). Write down...
- 15M.1.sl.TZ2.1a: Find the distance from \({\text{P}}(100,{\text{ }}200)\) to \({\text{A}}\). Give your answer...
- 15M.1.sl.TZ2.2c: Fabián estimates that the distance from the base of the building to the car is 150 metres....
- 15M.1.sl.TZ2.10a: Find the amount of money that Minta will have in the bank after 3 years. Give your answer...
- 15M.2.sl.TZ2.6c: Estimate the total cost, to the nearest USD, of producing \(13\) bicycles on a particular day.
- 14N.2.sl.TZ0.4a: (i) Find the size of angle \({\rm{ACB}}\). (ii) Show that the size of angle...
- 16N.2.sl.TZ0.3d: Show that the equation of \({L_2}\) is \(2y + x - 19 = 0\).
- 16N.1.sl.TZ0.8b: Use the information about the cost of tickets to write down a second equation in \(x\) and...
- 17M.1.sl.TZ2.6c.ii: Before measuring, the researcher estimated \(k\) to be approximately 9.5 cm. Find the...
- 11N.1.sl.TZ0.1b.i: Write your answer to part (a) correct to 2 decimal places.
- 11N.1.sl.TZ0.1b.ii: Write your answer to part (a) correct to three significant figures.
- 11M.1.sl.TZ1.1c: Calculate the percentage error in Barry’s estimate of the value of \(p\) .
- 13M.1.sl.TZ1.1b: Write down your answer to part (a) (i) correct to the nearest 1000 ; (ii) correct to three...
- 07M.2.sl.TZ0.4ii.e: Using your results from parts (a) to (c), or otherwise, calculate the sum of the first 10...
- 08M.1.sl.TZ2.11c: Find how many Norwegian Kroner there are to the Euro. Give your answer correct to 2 decimal...
- 14M.1.sl.TZ1.1b: Write down your answer to part (a) (i) correct to two decimal places; (ii) correct...
- 15M.1.sl.TZ1.10a: Calculate the value of Pierre’s investment at the end of this time. Give your answer correct...
- 16N.2.sl.TZ0.3c: Find the length of AC.
- 16N.1.sl.TZ0.1b: Write your answer to part (a) (i) correct to two decimal places; (ii) correct to...
- 16N.2.sl.TZ0.3g: Find the area of ABCD.
- 17M.2.sl.TZ1.1d: Use your regression line to estimate the average weight of the brain of grey wolves.
- 18M.1.sl.TZ1.1b: Calculate the percentage error in the owner’s claim.
- 18M.2.sl.TZ2.5a.ii: Use Giovanni's diagram to calculate the length of AX.
- 12M.2.sl.TZ1.3b: Show that the volume of the metal used in the cylinder is 402 cm3, given correct to three...
- 11M.2.sl.TZ1.5e: She sells the land for \(120\) USD per square metre. Calculate the value of the land that...
- 13M.1.sl.TZ1.11c: At the airport in Vietnam, Neung changes 150 USD into Vietnamese dong (VND) to pay for her...
- 13M.2.sl.TZ1.3i: Find the percentage error in this estimate of the temperature of the coffee at t = 3.
- 13M.1.sl.TZ2.1b: Write your answer to part (a) correct to (i) one decimal place; (ii) three significant...
- 13M.1.sl.TZ2.12b: Yoshi spends 426.70 EUR in Italy. In an American bank he changes the remaining amount, into...
- 07M.1.sl.TZ0.3a: 1 Brazilian Real (BRL) = 2.607 South African Rand (ZAR). Giving answers correct to two...
- 07N.2.sl.TZ0.4ii.c: Find the expected frequency for the number of females who had ‘Comedy’ as their most-watched...
- 07N.1.sl.TZ0.6b: Calculate the value of Ben’s investment at the end of 6 years. Give your answer correct to 2...
- 14N.1.sl.TZ0.6a: Find the amount of the interest that Mandzur must pay. Give your answer correct to the...
- 16N.1.sl.TZ0.8a: Use the above information to write down an equation in \(x\) and \(y\).
- 17N.2.sl.TZ0.3b: Calculate angle \({\rm{B\hat CD}}\).
- 17N.2.sl.TZ0.3c: Find the area of ABCD.
- 18M.2.sl.TZ2.5c: Giovanni adds a point D to his diagram, such that BD = 45 m, and another triangle is...

