| Date | May 2017 | Marks available | 2 | Reference code | 17M.2.sl.TZ1.1 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Describe | Question number | 1 | Adapted from | N/A |
Question
The following table shows the average body weight, \(x\), and the average weight of the brain, \(y\), of seven species of mammal. Both measured in kilograms (kg).
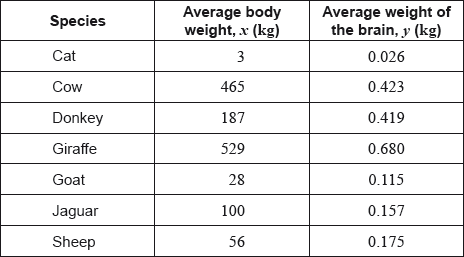
The average body weight of grey wolves is 36 kg.
In fact, the average weight of the brain of grey wolves is 0.120 kg.
The average body weight of mice is 0.023 kg.
Find the range of the average body weights for these seven species of mammal.
For the data from these seven species calculate \(r\), the Pearson’s product–moment correlation coefficient;
For the data from these seven species describe the correlation between the average body weight and the average weight of the brain.
Write down the equation of the regression line \(y\) on \(x\), in the form \(y = mx + c\).
Use your regression line to estimate the average weight of the brain of grey wolves.
Find the percentage error in your estimate in part (d).
State whether it is valid to use the regression line to estimate the average weight of the brain of mice. Give a reason for your answer.
Markscheme
\(529 - 3\) (M1)
\( = 526{\text{ (kg)}}\) (A1)(G2)
[2 marks]
\(0.922{\text{ }}(0.921857 \ldots )\) (G2)
[2 marks]
(very) strong, positive (A1)(ft)(A1)(ft)
Note: Follow through from part (b)(i).
[2 marks]
\(y = 0.000986x + 0.0923{\text{ }}(y = 0.000985837 \ldots x + 0.0923391…)\) (A1)(A1)
Note: Award (A1) for \(0.000986x\), (A1) for 0.0923.
Award a maximum of (A1)(A0) if the answer is not an equation in the form \(y = mx + c\).
[2 marks]
\(0.000985837 \ldots (36) + 0.0923391 \ldots \) (M1)
Note: Award (M1) for substituting 36 into their equation.
\(0.128{\text{ (kg) }}\left( {0.127829 \ldots {\text{ (kg)}}} \right)\) (A1)(ft)(G2)
Note: Follow through from part (c). The final (A1) is awarded only if their answer is positive.
[2 marks]
\(\left| {\frac{{0.127829 \ldots - 0.120}}{{0.120}}} \right| \times 100\) (M1)
Note: Award (M1) for their correct substitution into percentage error formula.
\(6.52{\text{ }}(\% ){\text{ }}\left( {6.52442...{\text{ }}(\% )} \right)\) (A1)(ft)(G2)
Note: Follow through from part (d). Do not accept a negative answer.
[2 marks]
Not valid (A1)
the mouse is smaller/lighter/weighs less than the cat (lightest mammal) (R1)
OR
as it would mean the mouse’s brain is heavier than the whole mouse (R1)
OR
0.023 kg is outside the given data range. (R1)
OR
Extrapolation (R1)
Note: Do not award (A1)(R0). Do not accept percentage error as a reason for validity.
[2 marks]

