| Date | May 2015 | Marks available | 2 | Reference code | 15M.1.sl.TZ2.2 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Calculate | Question number | 2 | Adapted from | N/A |
Question
Fabián stands on top of a building, T, which is on a horizontal street.
He observes a car, C, on the street, at an angle of depression of 30°. The base of the building is at B. The height of the building is 80 metres.
The following diagram indicates the positions of T, B and C.
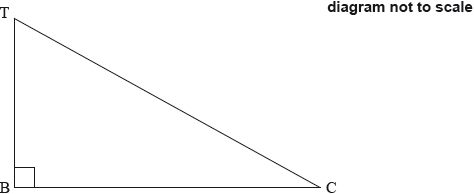
Show, in the appropriate place on the diagram, the values of
(i) the height of the building;
(ii) the angle of depression.
Find the distance, BC, from the base of the building to the car.
Fabián estimates that the distance from the base of the building to the car is 150 metres. Calculate the percentage error of Fabián’s estimate.
Markscheme
(A1)(A1) (C2)
Notes: Award (A1) for 80 m in the correct position on diagram.
Award (A1) for 30° in a correct position on diagram.
\(\tan 30^\circ = \frac{{80}}{{{\text{BC}}}}\;\;\;\)OR\(\;\;\;\tan 60^\circ = \frac{{{\text{BC}}}}{{80}}\;\;\;\)OR\(\;\;\;\frac{{80}}{{\sin 30^\circ }} = \frac{{{\text{BC}}}}{{\sin 60^\circ }}\) (M1)
Note: Award (M1) for a correct trigonometric or Pythagorean equation for BC with correctly substituted values.
\(({\text{BC}} = ){\text{ 139 (m)}}\;\;\;\left( {138.564 \ldots {\text{ (m)}}} \right)\) (A1)(ft) (C2)
Notes: Accept an answer of \(80\sqrt 3 \) which is the exact answer.
Follow through from part (a).
Do not penalize use of radians unless it leads to a negative answer.
\(\left| {\frac{{150 - 138.564 \ldots }}{{138.564 \ldots }}} \right| \times 100\) (M1)
Notes: Award (M1) for their correct substitution into the percentage error formula.
\( = 8.25(\% )\;\;\;(8.25317 \ldots \% )\) (A1)(ft) (C2)
Notes: Accept \(7.91(\%)\) (\(7.91366...\) if \(139\) is used.
Accept \(8.23(\%)\) (\(8.22510...\) if \(138.6\) is used.
Follow through from their answer to part (b).
If answer to part (b) is \(46.2\), answer to part (c) is \(225\%\), award (M1)(A1)(ft) with or without working seen. If answer to part (b) is negative, award at most (M1)(A0).

