| Date | May 2010 | Marks available | 3 | Reference code | 10M.2.sl.TZ1.9 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 9 | Adapted from | N/A |
Question
Let \(f(x) = A{{\rm{e}}^{kx}} + 3\) . Part of the graph of f is shown below.
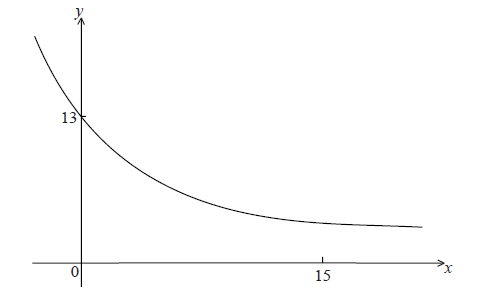
The y-intercept is at (0, 13) .
Show that \(A = 10\) .
Given that \(f(15) = 3.49\) (correct to 3 significant figures), find the value of k.
(i) Using your value of k , find \(f'(x)\) .
(ii) Hence, explain why f is a decreasing function.
(iii) Write down the equation of the horizontal asymptote of the graph f .
Let \(g(x) = - {x^2} + 12x - 24\) .
Find the area enclosed by the graphs of f and g .
Markscheme
substituting (0, 13) into function M1
e.g. \(13 = A{{\rm{e}}^0} + 3\)
\(13 = A + 3\) A1
\(A = 10\) AG N0
[2 marks]
substituting into \(f(15) = 3.49\) A1
e.g. \(3.49 = 10{{\rm{e}}^{15k}} + 3\) , \(0.049 = {{\rm{e}}^{15k}}\)
evidence of solving equation (M1)
e.g. sketch, using \(\ln \)
\(k = - 0.201\) (accept \(\frac{{\ln 0.049}}{{15}}\) ) A1 N2
[3 marks]
(i) \(f(x) = 10{{\rm{e}}^{ - 0.201x}} + 3\)
\(f(x) = 10{{\rm{e}}^{ - 0.201x}} \times - 0.201\) \(( = - 2.01{{\rm{e}}^{ - 0.201x}})\) A1A1A1 N3
Note: Award A1 for \(10{{\rm{e}}^{ - 0.201x}}\) , A1 for \( \times - 0.201\) , A1 for the derivative of 3 is zero.
(ii) valid reason with reference to derivative R1 N1
e.g. \(f'(x) < 0\) , derivative always negative
(iii) \(y = 3\) A1 N1
[5 marks]
finding limits \(3.8953 \ldots \), \(8.6940 \ldots \) (seen anywhere) A1A1
evidence of integrating and subtracting functions (M1)
correct expression A1
e.g. \(\int_{3.90}^{8.69} {g(x) - f(x){\rm{d}}x} \) , \(\int_{3.90}^{8.69} {\left[ {\left( { - {x^2} + 12x - 24} \right) - \left( {10{{\rm{e}}^{ - 0.201x}} + 3} \right)} \right]} {\rm{d}}x\)
area \(= 19.5\) A2 N4
[6 marks]
Examiners report
This question was quite well done by a great number of candidates indicating that calculus is a topic that is covered well by most centres. Parts (a) and (b) proved very accessible to many candidates.
This question was quite well done by a great number of candidates indicating that calculus is a topic that is covered well by most centres. Parts (a) and (b) proved very accessible to many candidates.
The chain rule in part (c) was also carried out well. Few however, recognized the command term “hence” and that \(f'(x) < 0\) guarantees a decreasing function. A common answer for the equation of the asymptote was to give \(y = 0\) or \(x = 3\) .
In part (d), it was again surprising and somewhat disappointing to see how few candidates were able to use their GDC effectively to find the area between curves, often not finding correct limits, and often trying to evaluate the definite integral without the GDC, which led nowhere.

