| Date | May 2009 | Marks available | 8 | Reference code | 09M.1.sl.TZ1.8 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find, Hence, and Justify | Question number | 8 | Adapted from | N/A |
Question
A rectangle is inscribed in a circle of radius 3 cm and centre O, as shown below.
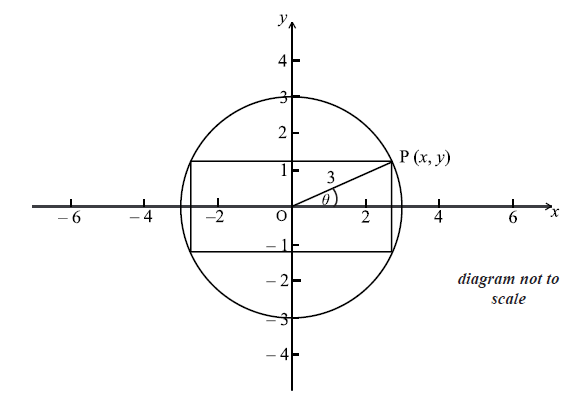
The point P(x , y) is a vertex of the rectangle and also lies on the circle. The angle between (OP) and the x-axis is \(\theta \) radians, where \(0 \le \theta \le \frac{\pi }{2}\) .
Write down an expression in terms of \(\theta \) for
(i) \(x\) ;
(ii) \(y\) .
Let the area of the rectangle be A.
Show that \(A = 18\sin 2\theta \) .
(i) Find \(\frac{{{\rm{d}}A}}{{{\rm{d}}\theta }}\) .
(ii) Hence, find the exact value of \(\theta \) which maximizes the area of the rectangle.
(iii) Use the second derivative to justify that this value of \(\theta \) does give a maximum.
Markscheme
(i) \(x = 3\cos \theta \) A1 N1
(ii) \(y = 3\sin \theta \) A1 N1
[2 marks]
finding area (M1)
e.g. \(A = 2x \times 2y\) , \(A = 8 \times \frac{1}{2}bh\)
substituting A1
e.g. \(A = 4 \times 3\sin \theta \times 3\cos \theta \) , \(8 \times \frac{1}{2} \times 3\cos \theta \times 3\sin \theta \)
\(A = 18(2\sin \theta \cos \theta )\) A1
\(A = 18\sin 2\theta \) AG N0
[3 marks]
(i) \(\frac{{{\rm{d}}A}}{{{\rm{d}}\theta }} = 36\cos 2\theta \) A2 N2
(ii) for setting derivative equal to 0 (M1)
e.g. \(36\cos 2\theta = 0\) , \(\frac{{{\rm{d}}A}}{{{\rm{d}}\theta }} = 0\)
\(2\theta = \frac{\pi }{2}\) (A1)
\(\theta = \frac{\pi }{4}\) A1 N2
(iii) valid reason (seen anywhere) R1
e.g. at \(\frac{\pi }{4}\), \(\frac{{{{\rm{d}}^2}A}}{{{\rm{d}}{\theta ^2}}} < 0\) ; maximum when \(f''(x) < 0\)
finding second derivative \(\frac{{{{\rm{d}}^2}A}}{{{\rm{d}}{\theta ^2}}} = - 72\sin 2\theta \) A1
evidence of substituting \(\frac{\pi }{4}\) M1
e.g. \( - 72\sin \left( {2 \times \frac{\pi }{4}} \right)\) , \( - 72\sin \left( {\frac{\pi }{2}} \right)\) , \( - 72\)
\(\theta = \frac{\pi }{4}\) produces the maximum area AG N0
[8 marks]
Examiners report
Candidates familiar with the circular nature of sine and cosine found part (a) accessible. However, a good number of candidates left this part blank, which suggests that there was difficulty interpreting the meaning of the x and y in the diagram.
Those with answers from (a) could begin part (b), but many worked backwards and thus earned no marks. In a "show that" question, a solution cannot begin with the answer given. The area of the rectangle could be found by using \(2x \times 2y\) , or by using the eight small triangles, but it was essential that the substitution of the double-angle formula was shown before writing the given answer.
As the area function was given in part (b), many candidates correctly found the derivative in (c) and knew to set this derivative to zero for a maximum value. Many gave answers in degrees, however, despite the given domain in radians.
Although some candidates found the second derivative function correctly, few stated that the second derivative must be negative at a maximum value. Simply calculating a negative value is not sufficient for a justification.

