| Date | November 2010 | Marks available | 7 | Reference code | 10N.1.sl.TZ0.10 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find, Show that, and Hence | Question number | 10 | Adapted from | N/A |
Question
Let f(x)=x3. The following diagram shows part of the graph of f .
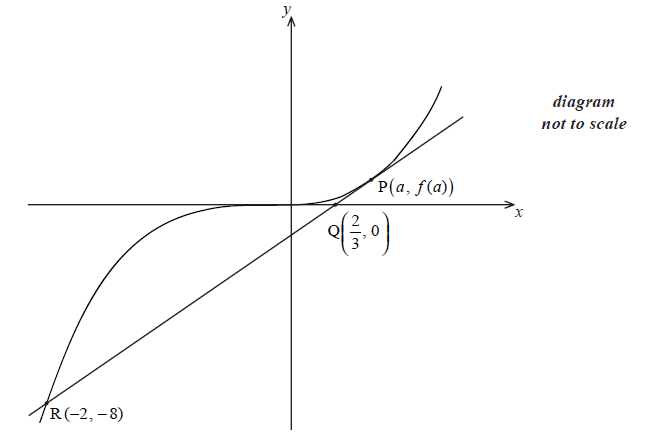
The point P(a,f(a)) , where a>0 , lies on the graph of f . The tangent at P crosses the x-axis at the point Q(23,0) . This tangent intersects the graph of f at the point R(−2, −8) .
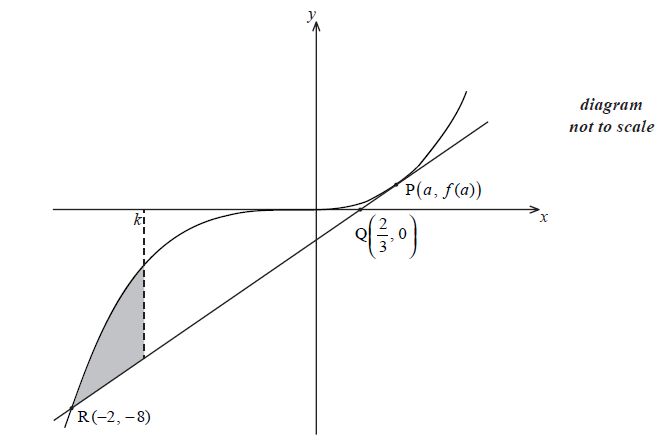
The equation of the tangent at P is y=3x−2 . Let T be the region enclosed by the graph of f , the tangent [PR] and the line x=k , between x=−2 and x=k where −2<k<1 . This is shown in the diagram below.
(i) Show that the gradient of [PQ] is a3a−23 .
(ii) Find f′(a) .
(iii) Hence show that a=1 .
Given that the area of T is 2k+4 , show that k satisfies the equation k4−6k2+8=0 .
Markscheme
(i) substitute into gradient =y1−y2x1−x2 (M1)
e.g. f(a)−0a−23
substituting f(a)=a3
e.g. a3−0a−23 A1
gradient a3a−23 AG N0
(ii) correct answer A1 N1
e.g. 3a2 , f′(a)=3 , f′(a)=a3a−23
(iii) METHOD 1
evidence of approach (M1)
e.g. f′(a)=gradient , 3a2=a3a−23
simplify A1
e.g. 3a2(a−23)=a3
rearrange A1
e.g. 3a3−2a2=a3
evidence of solving A1
e.g. 2a3−2a2=2a2(a−1)=0
a=1 AG N0
METHOD 2
gradient RQ =−8−2−23 A1
simplify A1
e.g. −8−83,3
evidence of approach (M1)
e.g. f′(a)=gradient , 3a2=−8−2−23 , a3a−23=3
simplify A1
e.g. 3a2=3 , a2=1
a=1 AG N0
[7 marks]
approach to find area of T involving subtraction and integrals (M1)
e.g. ∫f−(3x−2)dx , ∫k−2(3x−2)−∫k−2x3 , ∫(x3−3x+2)
correct integration with correct signs A1A1A1
e.g. 14x4−32x2+2x , 32x2−2x−14x4
correct limits −2 and k (seen anywhere) A1
e.g. ∫k−2(x3−3x+2)dx , [14x4−32x2+2x]k−2
attempt to substitute k and −2 (M1)
correct substitution into their integral if 2 or more terms A1
e.g. (14k4−32k2+2k)−(4−6−4)
setting their integral expression equal to 2k+4 (seen anywhere) (M1)
simplifying A1
e.g. 14k4−32k2+2=0
k4−6k2+8=0 AG N0
[9 marks]
Examiners report
Part (a) seemed to be well-understood by many candidates, and most were able to earn at least partial marks here. Part (ai) was a "show that" question, and unfortunately there were some candidates who did not show how they arrived at the given expression.
In part (b), the concept seemed to be well-understood. Most candidates saw the necessity of using definite integrals and subtracting the two functions, and the integration was generally done correctly. However, there were a number of algebraic and arithmetic errors which prevented candidates from correctly showing the desired final result.
