| Date | May 2008 | Marks available | 4 | Reference code | 08M.2.sl.TZ1.10 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 10 | Adapted from | N/A |
Question
The following diagram shows the graphs of \(f(x) = \ln (3x - 2) + 1\) and \(g(x) = - 4\cos (0.5x) + 2\) , for \(1 \le x \le 10\) .
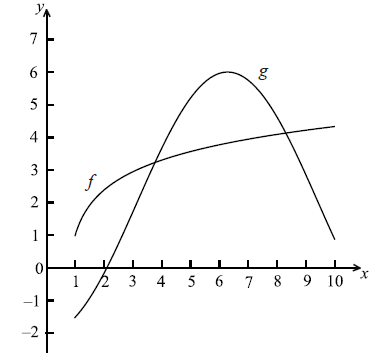
Let A be the area of the region enclosed by the curves of f and g.
(i) Find an expression for A.
(ii) Calculate the value of A.
(i) Find \(f'(x)\) .
(ii) Find \(g'(x)\) .
There are two values of x for which the gradient of f is equal to the gradient of g. Find both these values of x.
Markscheme
(i) intersection points \(x = 3.77\) , \(x = 8.30\) (may be seen as the limits) (A1)(A1)
approach involving subtraction and integrals (M1)
fully correct expression A2
e.g. \(\int_{3.77}^{8.30} {(( - 4\cos (0.5x) + 2) - (\ln (3x - 2) + 1)){\rm{d}}x} \) , \(\int_{3.77}^{8.30} {g(x){\rm{d}}x - } \int_{3.77}^{8.30} {f(x){\rm{d}}x} \)
(ii) \(A = 6.46\) A1 N1
[6 marks]
(i) \(f'(x) = \frac{3}{{3x - 2}}\) A1A1 N2
Note: Award A1 for numerator (3), A1 for denominator (\({3x - 2}\)) , but penalize 1 mark for additional terms.
(ii) \(g'(x) = 2\sin (0.5x)\) A1A1 N2
Note: Award A1 for 2, A1 for \(\sin (0.5x)\) , but penalize 1 mark for additional terms.
[4 marks]
evidence of using derivatives for gradients (M1)
correct approach (A1)
e.g. \(f'(x) = g'(x)\) , points of intersection
\(x = 1.43\) , \(x = 6.10\) A1A1 N2N2
[4 marks]
Examiners report
Many candidates did not make good use of the GDC in this problem. Most had the correct expression but incorrect limits. Some tried to integrate to find the area without using their GDC. This became extremely complicated and time consuming.
In part (b), the chain rule was not used by some.
Most candidates realized the relationship between the gradient and the first derivative and set the two derivatives equal to one another. Once again many did not realize that the intersection could be easily found on their GDC.

