| Date | May 2009 | Marks available | 2 | Reference code | 09M.2.sl.TZ2.10 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Write down | Question number | 10 | Adapted from | N/A |
Question
Let \(f(x) = 3\sin x + 4\cos x\) , for \( - 2\pi \le x \le 2\pi \) .
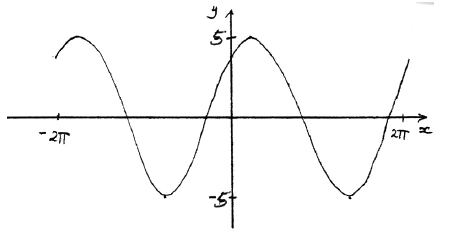
Sketch the graph of f .
Write down
(i) the amplitude;
(ii) the period;
(iii) the x-intercept that lies between \( - \frac{\pi }{2}\) and 0.
Hence write \(f(x)\) in the form \(p\sin (qx + r)\) .
Write down one value of x such that \(f'(x) = 0\) .
Write down the two values of k for which the equation \(f(x) = k\) has exactly two solutions.
Let \(g(x) = \ln (x + 1)\) , for \(0 \le x \le \pi \) . There is a value of x, between \(0\) and \(1\), for which the gradient of f is equal to the gradient of g. Find this value of x.
Markscheme
 A1A1A1 N3
A1A1A1 N3
Note: Award A1 for approximately sinusoidal shape, A1 for end points approximately correct \(( - 2\pi {\text{, }}4)\) \((2\pi {\text{, }}4)\), A1 for approximately correct position of graph, (y-intercept \((0{\text{, }}4)\), maximum to right of y-axis).
[3 marks]
(i) 5 A1 N1
(ii) \(2\pi \) (6.28) A1 N1
(iii) \( - 0.927\) A1 N1
[3 marks]
\(f(x) = 5\sin (x + 0.927)\) (accept \(p = 5\) , \(q = 1\) , \(r = 0.927\) ) A1A1A1 N3
[3 marks]
evidence of correct approach (M1)
e.g. max/min, sketch of \(f'(x)\) indicating roots
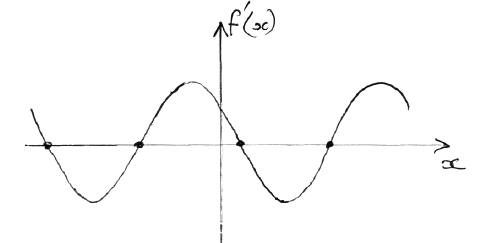
one 3 s.f. value which rounds to one of \( - 5.6\), \( - 2.5\), \(0.64\), \(3.8\) A1 N2
[2 marks]
\(k = - 5\) , \(k = 5\) A1A1 N2
[2 marks]
METHOD 1
graphical approach (but must involve derivative functions) M1
e.g.
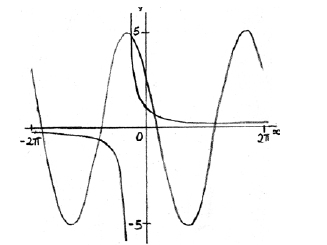
each curve A1A1
\(x = 0.511\) A2 N2
METHOD 2
\(g'(x) = \frac{1}{{x + 1}}\) A1
\(f'(x) = 3\cos x - 4\sin x\) \((5\cos (x + 0.927))\) A1
evidence of attempt to solve \(g'(x) = f'(x)\) M1
\(x = 0.511\) A2 N2
[5 marks]
Examiners report
Some graphs in part (a) were almost too detailed for just a sketch but more often, the important features were far from clear. Some graphs lacked scales on the axes.
A number of candidates had difficulty finding the period in part (b)(ii).
A number of candidates had difficulty writing the correct value of q in part (c).
The most common approach in part (d) was to differentiate and set \(f'(x) = 0\) . Fewer students found the values of x given by the maximum or minimum values on their graphs.
Part (e) proved challenging for many candidates, although if candidates answered this part, they generally did so correctly.
In part (f), many candidates were able to get as far as equating the two derivatives but fewer used their GDC to solve the resulting equation. Again, many had trouble demonstrating their method of solution.

