| Date | May 2010 | Marks available | 6 | Reference code | 10M.1.sl.TZ1.8 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Write down | Question number | 8 | Adapted from | N/A |
Question
Let \(f(x) = \frac{1}{2}{x^3} - {x^2} - 3x\) . Part of the graph of f is shown below.
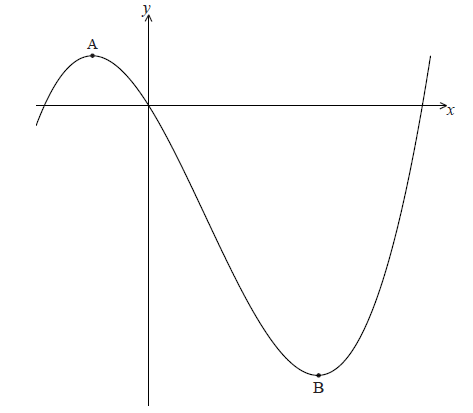
There is a maximum point at A and a minimum point at B(3, − 9) .
Find the coordinates of A.
Write down the coordinates of
(i) the image of B after reflection in the y-axis;
(ii) the image of B after translation by the vector \(\left( {\begin{array}{*{20}{c}}
{ - 2}\\
5
\end{array}} \right)\) ;
(iii) the image of B after reflection in the x-axis followed by a horizontal stretch with scale factor \(\frac{1}{2}\) .
Markscheme
\(f(x) = {x^2} - 2x - 3\) A1A1A1
evidence of solving \(f'(x) = 0\) (M1)
e.g. \({x^2} - 2x - 3 = 0\)
evidence of correct working A1
e.g. \((x + 1)(x - 3)\) , \(\frac{{2 \pm \sqrt {16} }}{2}\)
\(x = - 1\) (ignore \(x = 3\) ) (A1)
evidence of substituting their negative x-value into \(f(x)\) (M1)
e.g. \(\frac{1}{3}{( - 1)^3} - {( - 1)^2} - 3( - 1)\) , \( - \frac{1}{3} - 1 + 3\)
\(y = \frac{5}{3}\) A1
coordinates are \(\left( { - 1,\frac{5}{3}} \right)\) N3
[8 marks]
(i) \(( - 3{\text{, }} - 9)\) A1 N1
(ii) \((1{\text{, }} - 4)\) A1A1 N2
(iii) reflection gives \((3{\text{, }}9)\) (A1)
stretch gives \(\left( {\frac{3}{2}{\text{, }}9} \right)\) A1A1 N3
[6 marks]
Examiners report
A majority of candidates answered part (a) completely.
Candidates were generally successful in finding images after single transformations in part (b). Common incorrect answers for (biii) included \(\left( {\frac{3}{2},\frac{9}{2}} \right)\) , (6, 9) and (6, 18) , demonstrating difficulty with images from horizontal stretches.

