| Date | May 2011 | Marks available | 4 | Reference code | 11M.1.sl.TZ2.9 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 9 | Adapted from | N/A |
Question
The following diagram shows part of the graph of a quadratic function f .
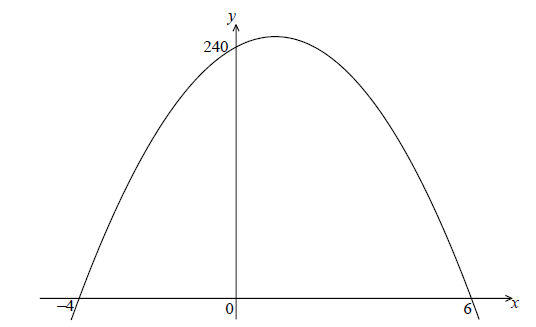
The x-intercepts are at \(( - 4{\text{, }}0)\) and \((6{\text{, }}0)\) , and the y-intercept is at \((0{\text{, }}240)\) .
Write down \(f(x)\) in the form \(f(x) = - 10(x - p)(x - q)\) .
Find another expression for \(f(x)\) in the form \(f(x) = - 10{(x - h)^2} + k\) .
Show that \(f(x)\) can also be written in the form \(f(x) = 240 + 20x - 10{x^2}\) .
A particle moves along a straight line so that its velocity, \(v{\text{ m}}{{\text{s}}^{ - 1}}\) , at time t seconds is given by \(v = 240 + 20t - 10{t^2}\) , for \(0 \le t \le 6\) .
(i) Find the value of t when the speed of the particle is greatest.
(ii) Find the acceleration of the particle when its speed is zero.
Markscheme
\(f(x) = - 10(x + 4)(x - 6)\) A1A1 N2
[2 marks]
METHOD 1
attempting to find the x-coordinate of maximum point (M1)
e.g. averaging the x-intercepts, sketch, \(y' = 0\) , axis of symmetry
attempting to find the y-coordinate of maximum point (M1)
e.g. \(k = - 10(1 + 4)(1 - 6)\)
\(f(x) = - 10{(x - 1)^2} + 250\) A1A1 N4
METHOD 2
attempt to expand \(f(x)\) (M1)
e.g. \( - 10({x^2} - 2x - 24)\)
attempt to complete the square (M1)
e.g. \( - 10({(x - 1)^2} - 1 - 24)\)
\(f(x) = - 10{(x - 1)^2} + 250\) A1A1 N4
[4 marks]
attempt to simplify (M1)
e.g. distributive property, \( - 10(x - 1)(x - 1) + 250\)
correct simplification A1
e.g. \( - 10({x^2} - 6x + 4x - 24)\) , \( - 10({x^2} - 2x + 1) + 250\)
\(f(x) = 240 + 20x - 10{x^2}\) AG N0
[2 marks]
(i) valid approach (M1)
e.g. vertex of parabola, \(v'(t) = 0\)
\(t = 1\) A1 N2
(ii) recognizing \(a(t) = v'(t)\) (M1)
\(a(t) = 20 - 20t\) A1A1
speed is zero \( \Rightarrow t = 6\) (A1)
\(a(6) = - 100\) (\({\text{m}}{{\text{s}}^{ - 2}}\)) A1 N3
[7 marks]
Examiners report
Parts (a) and (c) of this question were very well done by most candidates.
In part (b), many candidates attempted to use the method of completing the square, but were unsuccessful dealing with the coefficient of \( - 10\). Candidates who recognized that the x-coordinate of the vertex was 1, then substituted this value into the function from part (a), were generally able to earn full marks here.
Parts (a) and (c) of this question were very well done by most candidates.
In part (d), it was clear that many candidates were not familiar with the relationship between velocity and acceleration, and did not understand how those concepts were related to the graph which was given. A large number of candidates used time \(t = 1\) in part b(ii), rather than \(t = 6\) . To find the acceleration, some candidates tried to integrate the velocity function, rather than taking the derivative of velocity. Still others found the derivative in part b(i), but did not realize they needed to use it in part b(ii), as well.

