The Unit Circle is probably the most important topic to understand from the whole of trigonometry. Lots of the properties of the trigonometric functions can be found from the unit circle. All the work on this page will help us understand all of these properties. This is essential knowledge, for example, for us to be able to solve trigonometric equations.
On this page, you should learn about
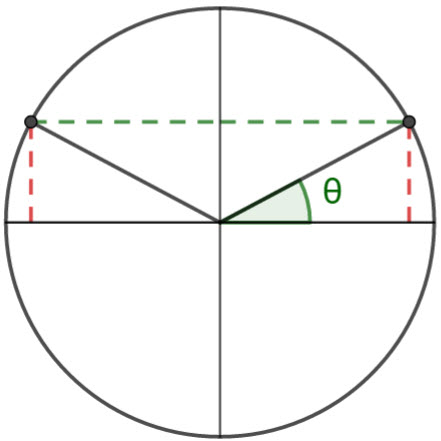
the definition of \(\sin \theta\) and \(\cos \theta\) in terms of the unit circle If we consider a unit circle (a circle of radius 1), then \(sin\theta=\frac{opposite}{hypotenuse}=\frac{opposite}{1}\)
\(cos\theta=\frac{adjacent}{hypotenuse}=\frac{adjacent}{1}\)
the definition of \(\tan \theta\) as \(\frac{opposite}{adjacent}=\frac{\sin\theta}{\cos\theta}\) exact values of trigonometric ratios of 0°, 30°, 45°, 60°, 90° the symmetry properties of graphs of trigonometric functions The following applets will help you understand the definition of sine and cosine in terms of the unit circle
sine of an angle is given by the opposite side , or the y coordinate on the unit circle
cosine of an angle is given by the adjacent side , or the x coordinate on the unit circle
Here is a quiz that practises the skills from this page
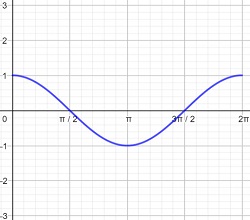
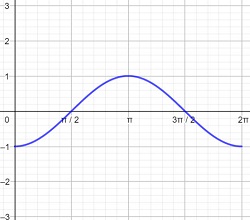
Drag the function next to the correct graph
sinx cos(-x) -cosx tanx -tanx -sinx sin(-x)
This question is about remembering the exact values for trigonometric ratios. Try to do it without your calculator.
Enter the correct angle. Each answer is an angle between 0 and 90°.
There is no need to enter the ° symbol
Drag the answers into the correct places
sin150° cos120° tan225° sin270° cos330° cos210°
Match up the following answers with their correct pair
Match up the following answers with their correct pair
Match up the following answers with their correct pair
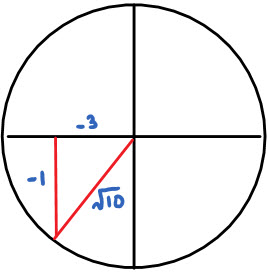
Given that \(tan\theta = \frac{1}{3}\) and \(\pi<\theta<\frac{3\pi}{2}\) , then
\(sin\theta\) =
\(\frac{a}{\sqrt{10}}\) \(cos\theta\) = \(\frac{b}{\sqrt{10}}\)
What are the values of a and b?
Given that \(sin\theta = \frac{3}{4}\) and \(90°< \theta <180°\) ,
find \(cos\theta\)
Given that \(cos\theta = \frac{3}{5}\) and \(\frac{3\pi}{2}<\theta<2\pi\) , then
\(sin\theta = \frac{a}{5}\)
\(tan\theta = \frac{b}{3}\)
What are the values of a and b?
Given that \(tan\theta = \frac{5}{12}\) and \(\pi<\theta<\frac{3\pi}{2}\) , then
\(sin\theta = \frac{a}{13}\)
\(cos\theta = \frac{b}{13}\)
What are the values of a, and b?
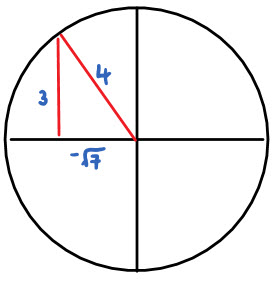
Given that \(cosx=-\frac{\sqrt{7}}{3}\) and \(\frac{\pi}{2}\le x\le \pi\) , find the possible values of sinx and tanx
Draw a circle.
x is in the second quadrant
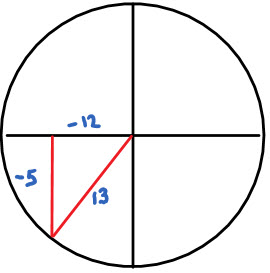
If \(tanx=\frac{12}{5}\) and \(\pi\le x\le \frac{3\pi}{2}\) , find the value of cosx
Draw a circle.
x is in the third quadrant
MY PROGRESS
Self-assessment How much of Unit CircleSL have you understood?
My notes
Which of the following best describes your feedback?







 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn