A polynomial function f(x) is an algebraic expression that takes the form
\({ f(x)=a }_{ n }{ x }^{ n }+{ a }_{ n-1 }{ x }^{ n-1 }+{ a }_{ n-2 }{ x }^{ n-2 }+\quad ...\quad +{ a }_{ 1 }{ x }^{ 1 }+{ a }_{ 0 }\)
For example, a polynomial function of degree 3 is a cubic function e.g \(f(x) = 7x^3+4x^2-3x+4\)
On this page, you should learn about
polynomial functions zeros, roots and factors the factor and remainder theorem The following videos will help you understand all the concepts from this page
The Remainder Theorem states that for a polynomial f(x),
the remainder when divided by (x-a) is f(a).
Example
Let \(f(x)=2x^3+4x^2+x-5\)
If we divide this polynomial by \((x-2)\) ...
\(\frac{2x^3+4x^2+x-5}{x-2}=2x^2+8x+17+\frac{29}{x-2}\)
... we get a quotient \(2x^2+8x+17\) and a remainder 29
When we work out f(2)...
\(f(2)=2(2)^3+4(2)^2+(2)-5=29\) ...
... we get 29
The factor theorem states that for a polynomial f(x),
(x-a) is a factor if and only if f(a)=0
Example
Let \(f(x)=x^4+2x^3-7x^2-8x+12\)
When we work out f(1)...
\(f(1)=(1)^4+2(1)^3-7(1)^2-8(1)+12 = 0\)
If we divide this polynomial by \((x-1)\) ...
\(\frac{x^4+2x^3-7x^2-8x+12}{x-1}=x^3+3x^2-4x-12\)
... there is no remainder, \((x-1)\) is a factor of the polynomial
In this video, we will look at an application of the factor theorem which is to factorize polynomials:
Factorize completely \(f(x)=2x^3+x^2-7x-6\)
Typical Exam-style Question
In the following video, we will look at a typical exam-style question:
The cubic polynomial \(f(x)=ax^3+bx^2-29x+60\) has a factor \((x+4)\) and leaves a remainder of 6 when divided by \((x-2)\) .
a. Find the value of a b
b. Factorize the polynomial
Here is a quiz that practises the skills from this page
Given that f(x) = x3 +6x2 +14x+15 , find f(1)
f(1) = 13 +6(1)2 +14(1)+15 = 36
Given that f(x) = x3 +6x2 +14x+15 , find f(-3)
f(-3) = (-3)3 +6(-3)2 +14(-3)+15 = -27 + 54 - 42 + 15 = 0
note that x - 3 would be a factor of this polynomial
Find the remainder when x3 + 2x2 - 5x - 6 is divided by x - 1
Let f(x) = x3 +2x2 -5x - 6
Remainder = f(1) = (1)3 +2(1)2 - 5(1) - 6 = 1 + 2 - 5 - 6 = -8
Find the remainder when x4 - 3x3 - 7x2 + 15x + 18 is divided by x + 2
Remainder = f(-2) = (-2)4 - 3(-2)3 - 7(-2)2 + 15(-2) + 18 = 16 + 24 - 28 - 30 +18 = 0
Hence x + 2 is a factor.
f(x) is a polynomial of degree 3
f(1) = 3
f(2) = -4
f(1.5) = 0
Which of the following statements is definitely true?
If \(f(\frac {3}{2})=0\) then \((x - \frac{3}{2})\) is a factor or (2x - 3)
f(x) is a polynomial of degree 3 and f(-1) = f(1) = f(2) = 0.
Which of the following could be the function f(x)?
f(-1) = 0 implies x + 1 is a factor
f(1) = 0 implies x - 1 is a factor
f(2) = 0 implies x - 2 is a factor
f(x) = (x + 1)(x - 1)(x - 2)
f(x) =(x² - 1)(x - 2)
f(x) is a polynomial of degree 4
f(-1) = f(2) = f(3) = 0
Which of the following could be a graph of f
The key piece of information is that the polynomial is of degree 4
Hence it has 4 roots with one repeated
The polynomial f(x) = 3x3 + ax2 + x - 10 is divisible by (x - 2). Find the value of a
If f(x) is divisible by (x - 2) , then (x - 2) is a factor.
f(2) = 3(2)3 + a(2)2 + (2) - 10 = 0
24 + 4a + 2 - 10 = 0
4a = -16
a = -4
When the polynomial f(x) = x4 + 4x3 - 2x2 - 12x + a
Find a
f(-1) = (-1)4 + 4(-1)3 - 2(-1)2 - 12(-1) + a
1 - 4 - 2 + 12 + a
a
a
Complete the gaps to make the following statements true
The cubic polynomial \(3x^3+ax^2+bx-12\) has a factor \((x-2)\) and leaves a remainder of -20 when divided by \((x-1)\) .
Find the value of a b
Use the Factor and Remainder Theorem
f(2)=0
f(1)=-20
Given that \(ax^3+bx^2+17x-6\) is exactly divisible by \((x-1)(x-2)\) , find the value of a b
Use the Factor and Remainder Theorem
f(1)=0
f(2)=0
It is given that \(f(x)=x^3+ax^2+bx+8\)
a. Given that \(x^2-4\) is a factor of \(f(x)\) , find the values of a b
b. Factorize \(f(x)\) into a product of linear factors.
c. Sketch the graph of \(y=f(x)\) labelling any stationary points and the x and y intercepts.
d. Hence state the range of values of k \(f(x)=k\) has exactly one root.
c. Notice that you are allowed to use your calculator in this question. You should be able to find the stationary points from the calculator.
d. Think of \(f(x)=k\) as a horizontal line. What values of k
MY PROGRESS
Self-assessment How much of Factor and Remainder Theorem have you understood?
My notes
Which of the following best describes your feedback?
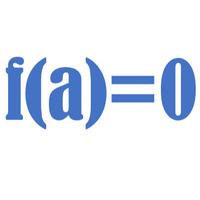 The Factor and Remainder Theorem form a small, but significant part of the course. It is not at all difficult, but it is worth reminding yourself of these theorem, since, in examinations students often forget them and waste a lot of time using long methods instead. The Factor Theorem is a theorem that allows us to find factors of polynomial functions, to find zeros and ultimately to help us sketch graphs.
The Factor and Remainder Theorem form a small, but significant part of the course. It is not at all difficult, but it is worth reminding yourself of these theorem, since, in examinations students often forget them and waste a lot of time using long methods instead. The Factor Theorem is a theorem that allows us to find factors of polynomial functions, to find zeros and ultimately to help us sketch graphs.






 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn