On this page, you should learn to
Understand the different types of relation: one-to-one function, many-to-one- function, one-to-many relation, many-to-many relation Use the domain and range of a function Find and use inverse functions \(f^{-1}\) Use composite functions \((f∘g)(x)=f(g(x))\) "Draw" and "Sketch" a graph Here is a quiz that tests your understanding of the basics of functions, the different types of relation, and also the domain and range of functions:
f(x) = 2x² - 1
Work out f(-1)
f(-1) = 2(-1)² - 1
f(-1) = 2(1) - 1=1
f(x) = 2x + 1
Work out f(3)
f(3) = 23 + 1
f(3) = 8 + 1 = 9
\(f(x)=\frac{2}{x-1}\)
\(f(a)=0.5\)
Work out a
\(\frac{2}{a-1}=0.5\)
2 = 0.5a - 0.5
2.5 = 0.5a
a = 5
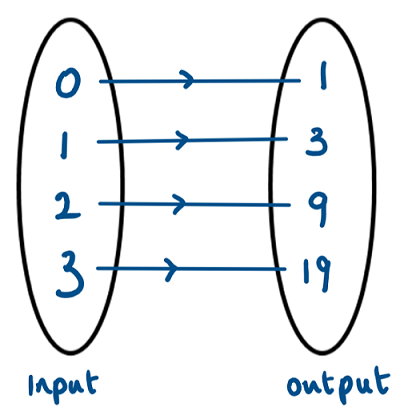
Which of the following best describes this relation?
Each input is mapped on to one and only one output
Which of the following best describes this relation?
Each possible output (except y = 1) has two corresponding inputs
E.g. 1→2, 3→2
Which of the following best describes this relation?
Each output has two inputs
Each input has two outputs
Which of the following is the domain of this function
The domain is all the possible inputs.
The inputs of this function are the set of real numbers (all real numbers are possible)
Which of the following is the range of this function
The range is all the possible outputs.
The outputs of this function are the set of real numbers except f(x) = 0 (all real numbers are possible except 0)
The range of the following function is a ≤ f(x) ≤ b
Find the values of a and b
The range is all the possible outputs.
Let \(f(x)=1-(x-2)^2\) , x ≥ k is a one-to-one function
Find the smallest value of k
The graph of the function with an unrestricted domain looks like this
For it to be a one-to-one function, we have to restrict the domain like this
...we can find the inverse of this function now
Here is a quiz that tests your understanding of composite and inverse functions
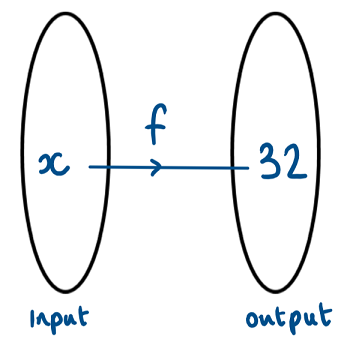
Let \(f(x)=\frac{x^3}{2}\)
Work out \(f^{-1}(32)\)
You do not have to work out the inverse function.
What is the input of the function f
\(\frac{x^3}{2}=32\)
x3 = 64
x = 4
Given that
f(x) = x + 1
g(x) = x² - 1
h(x) = 0.5x
Work out fgh(4)
There is no need to work out the composite function f(g(h(x)))
Make sure you do the functions in the correct order: 'do' h, then 'do' g, then 'do' f
h(4) = 0.5x4 = 2
g(2) = 2² - 1 = 3
f(3) = 3 + 1 = 4
The graph of y = f(x) is plotted.
The domain of f-1 is a ≤ x ≤ b
Work out a and b
The domain of f-1 is the range of f
This is all the possible outputs of the function f from the graph above (all possible y values)
The graph of y = f(x) is plotted.
Use it to work out
f-1 (1)
The output of f is 1. What is the input?
The graph of the function y = f(x) is plotted
Use it to work out f-1 (0)
The output of f is 0. What is the input?
Let f(x) = 2x - 1
The graph of y = g(x) is shown
Work out fg(1)
We 'do' g first
From the graph g(1) = 2
Then we 'do' f
f(2) = 2x2 - 1 = 3
Let f(x) = 2x
The graph of y = g(x) is shown
Work out gf(2)
We 'do' f first
f(2) = 22 = 4
Then, we 'do' g.
From the graph g(4) = 5
The graphs of y = f(x) and y = g(x) are plotted
Work out fg(2)
We 'do' g first:
From the graph g(2) = 3
Now we 'do' f:
From the graph f(3) = 7
The graph of y = f(x) is plotted
Let \(g(x)=\sqrt{x+3} \ , \ x \neq-3\)
Work out g(f-1 (-2))
From the graph, f-1 (-2) = 6
\(g(6)=\sqrt{6+3} =3\)
The graph of y = f(x) is plotted
Work out f-1 [f-1 (4)]
From the graph f-1 (4) = 1
From the graph f-1 (1) = -1
The function f g
\(f(x)=3x^2 \ ,\ x\in\mathbb{R}\)
\(g\left(x\right)=\frac{2}{x}-4\ ,x\in\mathbb{R},\ x>0\)
a) Find the range of g
b) Find g-1
c) Solve gf(x) = 2
a) To find the range, consider the graph of the function. What are all the possible y values?
c) Careful x > 0
Let f g f g
\(f(x)=ln(1-2x),x<\frac{1}{2}\)
\(g(x)=\frac{4}{x-2},x\neq2\)
a) Find the exact value of fg(-2)
b) Find f-1 (x), stating its domain
c) Show that \(gg(x)=\frac{4x-8}{8-2x}\)
b) domain of f-1 is the range of f
The graph of the function f
Use the graph to find values of
a) \(ff(-2)\)
b) \(f^{-1}(0)\)
Let g
c) Work out fg(1)
d) Draw a sketch of \(y=f^{-1}(x)\)
Think of this question in terms of inputs and outputs
f(-2) is the output from the function f when we input 2. From the graph, what is the y value, if the x value is -2?
f(-2) = 1
ff(-2) is the value that we get when the output from f(-2) becomes the new input into the function f
ff(-2) = 2
Let \(f(x)=\frac{ax-1}{x-a},\ x\neq\ a\)
a) Show that \(f^{-1}(x)=f(x)\)
b) Hence, find ff(b)
c) The graph of y = g(x) is shown below. Find the values of a
b) Notice the word 'hence'. This means that you should use what you found out in part a to answer this question
Let the function f
\(f(x)=\frac{x-k}{2-x},x\neq2\)
a) Find \(f^{-1}(x)\) in terms of k
b) Find k \(y=f(x)\) and \(y=f^{-1}(x)\) intersect at (-2 , -2) and (3 , 3)
Hint Solve \(f(x)=f^{-1}(x)\)
\(\frac{x-k}{2-x}=\frac{2x+k}{1+x}\)
Full Solution MY PROGRESS
Self-assessment How much of Functions - The Basics have you understood?
My notes
Which of the following best describes your feedback?
 In this page, we will look at the different types of relations including functions. The first step to gaining a good understanding of functions is to think about inputs and outputs. Once that is clear, you should be able to deal with domain and range, as well as composite and inverse functions. For the IB examination, questions require you to have a strong conceptual understanding of functions, with questions often posed with graphs. You will be well prepared for that if you work through this page.
In this page, we will look at the different types of relations including functions. The first step to gaining a good understanding of functions is to think about inputs and outputs. Once that is clear, you should be able to deal with domain and range, as well as composite and inverse functions. For the IB examination, questions require you to have a strong conceptual understanding of functions, with questions often posed with graphs. You will be well prepared for that if you work through this page.








 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn