For the topic of transforming functions, we need to understand the effect of translating, reflecting and stretching has on functions. On this page, we will also consider graphs of \(|f(x)|\) , \(f(|x|)\) , \(\frac{1}{f(x)}\) as well as [f(x)]² . You may be asked to describe the transformations, sketch graphs or find the coordinates of points that have been transformed. Whilst technology can be a big help understanding these transformations, questions often require you to answer them without your graphical calculator.
On this page, you should learn about
- transformations of graphs
- vertical translations: \(y=f(x)+b\)
- horizontal translations: \(y=f(x-a)\)
- reflection in x axis: \(y=-f(x)\)
- reflection in y axis: \(y=f(-x)\)
- vertical stretch: \(y=af(x)\)
- horizontal stretch: \(y=f(ax)\)
- compositions of any of the above transformations
- the graphs of the functions
- \(y=|f(x)|\)
- \(y=f(|x|)\)
- \(y=\frac{1}{f(x)}\)
- \(y=[f(x)]^2\)
- \(y=f(ax+b)\)
These graphs should help you understand the transformations of functions
Print from here
Here is a quiz that practises the transformations af(x) , f(ax), f(x)+a , f(x - a)
START QUIZ!
The graph of y = f(x) is transformed using translations and/or stretches. Describe the transformation from y = f(x) in each case below by dragging the description to the correct place
translate 2 units up translate 2 units down translate 2 units right translate 2 units left vertical stretch with scale factor 2 horizontal stretch with scale factor 2 horizontal stretch with scale factor 0.5 vertical stretch with scale factor 0.5
| f(x) + 2 | 2f(x) |
| f(x - 2) | f(2x) |
| f(0.5x) | f(x + 2) |
f(x - a) is translation a units right
f(x) + a is a traslation a units up
af(x) is a vertical stretch with scale factor a
f(ax) is a horizontal stretch with scale factor \(\frac{1}{a}\)
The graph of y = f(x) is transformed using translations and/or stretches. Describe the transformation from y = f(x) in each case below by dragging the function to the correct place
f(-x) -f(x) f(4x) 4f(x) f(0.25x) f(4x) 0.25f(x) f(x + 4) f(x - 4) f(x) + 4 f(x) - 4
| Reflection in the y axis | vertical stretch with scale factor 4 |
| horizontal stretch with scale factor 4 | translation of \(\left( \begin{matrix} 4 \\ 0 \end{matrix} \right) \) |
| translation of \(\left( \begin{matrix} 0 \\ -4 \end{matrix} \right) \) | Reflection in the x axis |
f(x - a) is translation a units right
f(x) + a is a traslation a units up
af(x) is a vertical stretch with scale factor a
f(ax) is a horizontal stretch with scale factor \(\frac{1}{a}\)
The graph of y = f(x) is transformed. Give the equation of the new graph after these transformations.
Careful, no stretch is NOT a stretch factor of zero!
| Vertical stretch scale factor 3 | y = af(bx) | a = b = |
| Translation of \(\left( \begin{matrix} 1 \\ 2 \end{matrix} \right) \) | y = f(x - a) + b | a = b = |
Vertical stretch factor 2 and horizontal stretch scale factor 2 | y = af(bx) | a = b = |
Reflection in the y axis and vertical stretch scale factor 4 | y = af(bx) | a = b= |
Vertical stretch scale factor 0.5, Reflection in the x axis and Translation of \(\left( \begin{matrix} -1 \\ -3 \end{matrix} \right) \) | y = af(bx - c) + d | a = b = c = d = |
Reflection in the x axis, Horizontal stretch scale factor 0.2 and Translation of \(\left( \begin{matrix} 0 \\ 2 \end{matrix} \right) \) | y = af(bx - c) + d | a = b = c = d = |
f(x - a) is translation a units right
f(x) + a is a traslation a units up
af(x) is a vertical stretch with scale factor a
f(ax) is a horizontal stretch with scale factor \(\frac{1}{a}\)
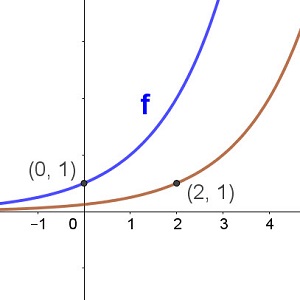
The graph of the function y = f(x) is plotted in blue in each of the graphs below. Match up the functions with the other graph in red
f(x + 2) f(x - 2) -f(x - 2) -f(x) + 2 f(x) - 2 -f(x) - 2
y=
| y=
| y=
|
y=
| y=
| y=
|
f(-x) is a reflection in the y axis
-f(x) is a reflection in the x axis
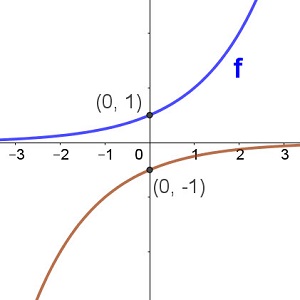
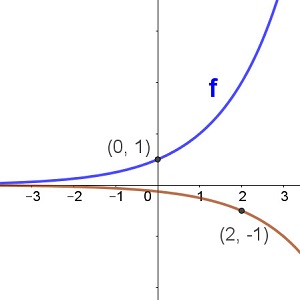
The graph of the function y = f(x) is plotted in blue in each of the graphs below. Match up the functions with the other graph in red
-f(x) f(x) - 2 f(x - 2) f(-x) -f(-x) -f(x - 2)
y =
| y =
| y =
|
y =
| y =
| y =
|
f(-x) is a reflection in the y axis
-f(x) is a reflection in the x axis
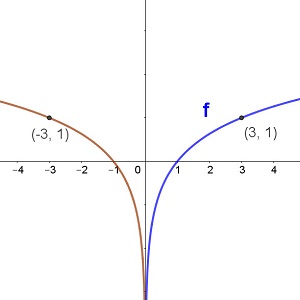
The graph of the function y = f(x) is plotted in blue in each of the graphs below. Match up the functions with the other graph in red
f(x) - 1 f(x - 2) f(-x) -f(x) f(x + 2) f(x) + 1
y =
| y =
| y =
|
y =
| y = 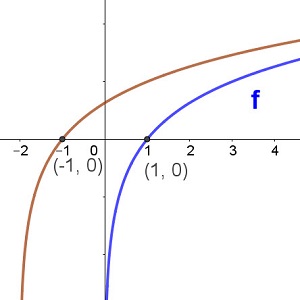 | y =  |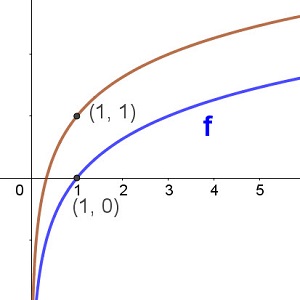
The graph of y = f(x) with the coordinates of A, B and C is shown below
Give the coordinates of A', B' and C' after the transformation 2f(-x)
A'(xA , yA)
xA = yA =
B'(xB , yB)
xB = yB =
C'(xC , yC)
xC = yC =
The transformation is
- Reflection in the y axis
- Vertical stretch scale factor 2
The graph of y = f(x) with the coordinates of A, B and C is shown below
Give the coordinates of A', B' and C' after the transformation f(-2x) + 1
A'(xA , yA)
xA = yA =
B'(xB , yB)
xB = yB =
C'(xC , yC)
xC = yC =
The transformation is
- Reflection in the x axis
- Horizontal stretch scale factor 0.5
- Translation of \(\left( \begin{matrix} 0 \\ 1 \end{matrix} \right) \)
The graph of y = f(x) with the coordinates of A, B and C is shown below
Give the coordinates of A', B' and C' after the transformation -f(x + 1) - 2
A'(xA , yA)
xA = yA =
B'(xB , yB)
xB = yB =
C'(xC , yC)
xC = yC =
The transformation is
- Translation of \(\left( \begin{matrix} -1 \\ 0 \end{matrix} \right) \)
- Reflection in x axis
- Translation of \(\left( \begin{matrix} 0 \\ -2 \end{matrix} \right) \)
Let f and g be the functions such that g(x) = -3f(2x +1) +1
The point A (2,5) on the graph of f is mapped to the point A' on the graph of g
Find A'
A'(xA , yA)
xA = yA =
The transformation is
- Horizontal stretch scale factor 0.5
- Translation of \(\left( \begin{matrix} -1 \\ 0 \end{matrix} \right) \)
- Reflection in x axis
- Vertical stretch scale factor 3
- Translation of \(\left( \begin{matrix} 0 \\ 1 \end{matrix} \right) \)
Here is a quiz for the transformation f(ax + b)
START QUIZ!
The graph of y = f(x) is plotted.
To draw the graph of \(y=f(\frac{1}{3}x+3)\), we should translate f(x) by \(\begin{pmatrix} c \\ 0 \end{pmatrix}\) followed by a stretch scale factor d from the y axis.
Find c and d
c =
d =
f(ax + b) is a translation \(\begin{pmatrix} -b \\ 0 \end{pmatrix}\) followed by a stretch scale factor \(\frac{1}{a}\) from the y axis
The graph of y = f(x) is plotted.
To draw the graph of \(y=f(\frac{1}{2}(x-3))\), we should stretch scale factor c from the y axis followed by a translation \(\begin{pmatrix} d \\ 0 \end{pmatrix}\)
Find c and d
c =
d =
\(y=f(a(x+b))\)is a stretch scale factor \(\frac{1}{a}\) from the y axis followed by a translation \(\begin{pmatrix} -b \\ 0 \end{pmatrix}\)
The graph of y = x² is translated 2 units to the left followed by a stretch scale factor 0.5 from the y axis.
What is the equation of the graph produced?
f(2x + 2) is a translation \(\begin{pmatrix} -2 \\ 0 \end{pmatrix}\) followed by a stretch scale factor \(\frac{1}{2}\) from the y axis
The graph of the function f(x) = lnx is shown.
The function is translated by \(\begin{pmatrix} 2 \\ 0 \end{pmatrix}\) then stretched by scale factor 2 from the y axis.
What is the new function?
f(ax + b) is a translation \(\begin{pmatrix} -b \\ 0 \end{pmatrix}\) followed by a stretch scale factor \(\frac{1}{a}\) from the y axis
The graph of y = x² is translated \(\begin{pmatrix} -1 \\ 0 \end{pmatrix}\) then stretched by a scale factor \(\frac{1}{3}\) from the y axis
Which of the following describes the equation of the new graph
f(ax + b) is a translation \(\begin{pmatrix} -b \\ 0 \end{pmatrix}\) followed by a stretch scale factor \(\frac{1}{a}\) from the y axis
Therefore
y = (3x + 1)² is a translation \(\begin{pmatrix} -1 \\ 0 \end{pmatrix}\) followed by a stretch scale factor \(\frac{1}{3}\) from the y axis
The graph of y = f(x) is shown in blue
If g(x) = f(0.5x - 2) which of the following shows the correct graph of y = g(x)
To get the graph g(x) = f(0.5x - 2) we start with f(x) then translate \(\begin{pmatrix}2\\ 0 \end{pmatrix}\) then stretch by scale factor 2 from the y axis. The maximum point goes from (0 , 4) to (2 , 4) to (4 , 4). Hence C.
The graph of y = f(x) is shown in blue
If g(x) = f(-2x + 1) which of the following shows the correct graph of y = g(x)
To get the graph g(x) = f(-2x + 1) we start with f(x) then translate \(\begin{pmatrix} -1\\ 0 \end{pmatrix}\) then stretch by scale factor 0.5 from the y axis and a reflection in the y axis. Point A goes from (2 , 3) to (1 , 3) to (0.5 , 3) to (-0.5 , 3). Hence D.
The graph of y = f(x) and y = (ax + b) are plotted below.
What are the values of a and b ?
a =
b =
f(ax + b) is a translation \(\begin{pmatrix} -b \\ 0 \end{pmatrix}\) followed by a stretch scale factor \(\frac{1}{a}\) from the y axis
f(-0.5x + 1) is a translation \(\begin{pmatrix} -1 \\ 0 \end{pmatrix}\) followed by a stretch scale factor 2 from the y axis and a reflection in the y axis
Two transformations are performed on a function:
A graph is translated 9 units right followed by a stretch scale factor \(\frac{1}{3}\) from the y axis.
This is the same as a stretch scale factor \(\frac{1}{3}\) from the y axis followed by a translation units right.
f(3(x - 3)) = f(3x - 9)
The graph of y = f(x) and y = (ax + b) are plotted below.
What are the values of a and b ?
a =
b =
f(ax + b) is a translation \(\begin{pmatrix} -b \\ 0 \end{pmatrix}\) followed by a stretch scale factor \(\frac{1}{a}\) from the y axis
f(2x - 1) is a translation \(\begin{pmatrix} 1 \\ 0 \end{pmatrix}\) followed by a stretch scale factor \(\frac{1}{2}\) from the y axis
Here's a quiz for the graphs of functions |f(x)| , f|x| , \({ 1\over f}\) and [f(x)]²
START QUIZ!
The graph of f(x) is shown in red
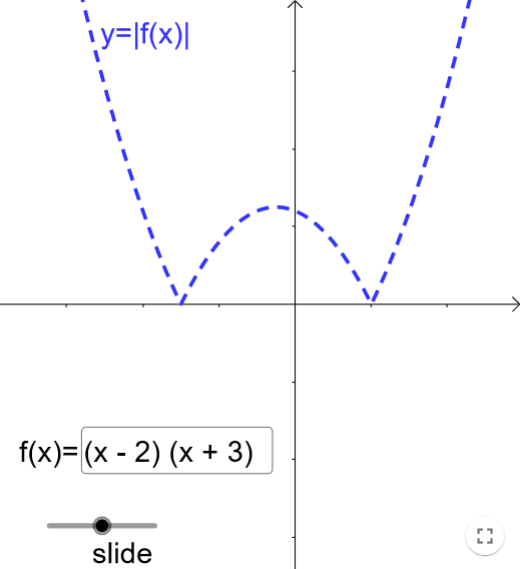
Which of the following below best represents the graph of f(|x|)
A
B
C
D
Any part of the function f to the right of the y axis is reflected in the y axis
The graph of f(x) is shown in green
Which of the following functions best represents the graph in red
The graph of f(x) = tanx and \(g(x)=\frac{1}{tanx}\), for \( (-\frac{\pi}{2}, \frac{\pi}{2} )\)
f(x) and \(1\over f(x)\) intersect when \(f(x)=\frac{1}{f(x)}=\pm 1\)
\(tan(\frac{\pi}{4})=1\\ tan(-\frac{\pi}{4})=-1\)
The graph of f(x) is shown in red
Which of the following functions best represents the graph in blue
any part of the function to the right of the y axis is reflected in the y axis
f(x) = cosx
Which of the following points lie on the graph of \(\frac{1}{f(x)}\)
Select all correct answers
The graph of f(x) is shown in red
Which of the following best represents a sketch of the graph of \(y= {1 \over f(x)}\)
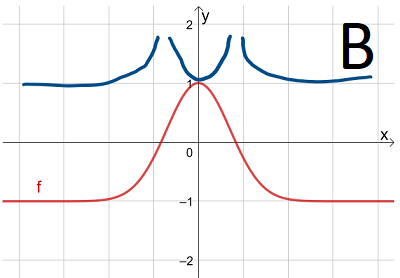
The x intercepts of y = f(x) become vertical asymptotes
The graph of y = f(x) and \(y= {1 \over f(x)}\) intersect where \(f(x)= \pm 1\)
Local maxima of f becomes local minima of \(y= {1 \over f(x)}\)
Hence D is the best sketch of \(y= {1 \over f(x)}\)
The graph of f(x) is shown in red
Which of the following represents the graph of y = [f(x)]²
The output of the function is squared.
As all outputs will be positive, there should be no part of the graph below the x axis
A
The graph of f(x) = sinx is shown in red
Which of the following represents the graph of y = [f(x)]²
The local maxima for f(x) = sinx is at \((\frac{\pi}{4},1)\).
Therefore the local maxima for [f(x)]² is at \((\frac{\pi}{4},1^2)\)...the same point.
The local minima for [f(x)]² is at \((-\frac{\pi}{4},1^2)\).
The answer could be B or C.
C is the graph of |f(x)|, since the shape of the curves is the same as f(x).
B is the correct answer because the outputs of [f(x)]²
The graph of f(x) is shown in red
Which of the following represents the graph of y = [f(x)]²
All outputs for [f(x)]² are positive so A is definitely wrong
f(x) goes through the point (1 , 1)
Hence, [f(x)]² goes through the point (1² , 1²) ...the same point.
Hence B is the correct answer.
The graph of y = f(x) is shown below
Which of the following is correct?
f(-1) < 1
Therefore, [f(-1)]² < |f(-1)|
And f(-1)]² < |f(-1)| < 1
f(1) < 1
Therefore \(\frac{1}{f(1)}>1\)
a) The following diagram shows the graph of a function f
On the same set of axes, sketch the graph of f(-x) + 2
You can print this graph from here
b)
The following diagram shows the function af(x+b)
Write down the values of a and b
Hint
Full Solution
The graph of f(x) has a local maxima at \((1 - a , 2b)\) and a local minima at \((3a,b-3)\).
a) Find the coordinates of the local maxima of \(f(x+a)-2b\)
b) Find the coordinates of the local minima of \(2f(3x)\)
Hint
Full Solution
Consider the function f(x) = x3 - 4x² - x + 6 , \(x \in \mathbb{R}\)
The graph of f is translated two units to the left and 3 units up to form the function g(x). Express g(x) in the form ax3 + bx² + cx + d where \(a,b,c,d \in \mathbb{Z}\)
Hint
Full Solution
The graph of \(y=e^{2x-1}\) is obtained by performing two transformations to the function \(f(x)=e^x\)
- a stretch of scale factor a parallel to the x axis
- a stretch of scale factor b parallel to the y axis.
Find the values of a and b
Hint
Full Solution
Consider the function f(x) = 2x² - 5x + 3
a) Factorise f(x)
b) Express f(x) in the form a(x - h)² + k
c) Hence, sketch the graph of \(\frac{1}{f(x)}\) indicating the equations of the asymptotes, the coordinates of any stationary points and the y intercept.
d) Sketch the graph of \(\frac{1}{f|x|}\)
Hint
Full Solution
How much of Transforming Functions HL have you understood?
Twitter 
Facebook 
LinkedIn