You will probably recognise the most commonly used form of the equation of a straight line: y = mx + c where m represents the gradient and c represents the y-intercept. It is important not to overlook this topic, as it comes up a lot in work on Functions, Vectors and Calculus. Make sure that you can use all three forms of the equation of a straight line, as this will help you with the Equation of Tangent and Normal.
On this page, you should learn to
Use the three different forms of the equations of straight lines \(y = mx + c \) \(ax+by + d = 0 \) \(y-y_1=m(x-x_1) \) Solve problems with parallel lines \(m_1=m_2\) Solve problems with perpendicular lines \(m_1 \times m_2=-1\) Here is a quiz that practises the skills from this page
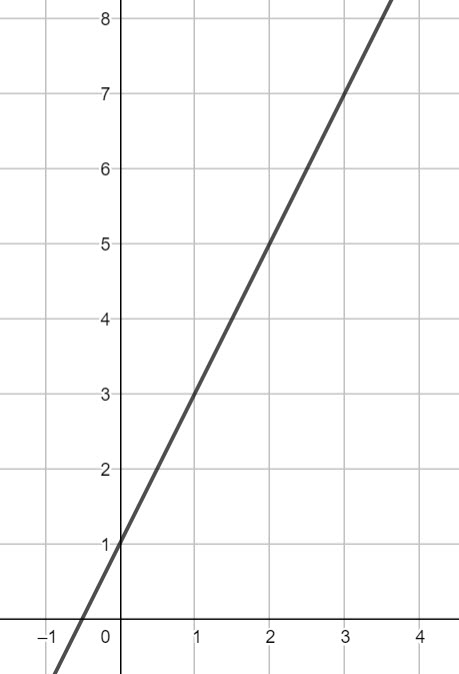
What is the gradient and y intercept of the following line?
gradient = \(\frac{rise}{run}\)
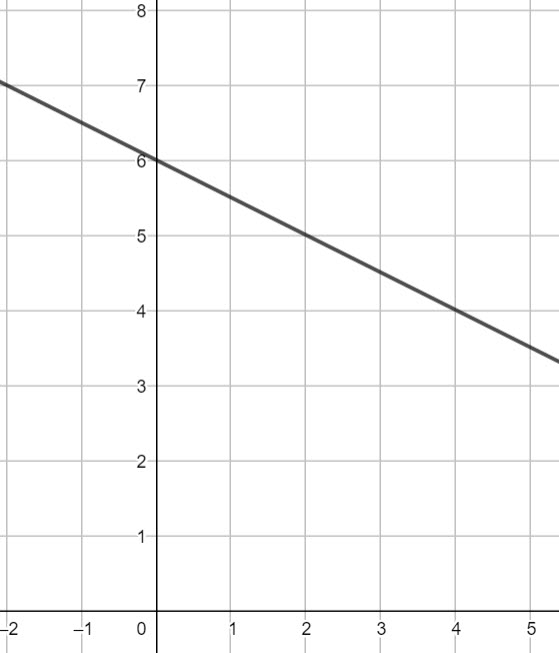
The equation of the following line can be written in the form \(y=ax+b\)
Find a b
a = gradient
b = y intercept
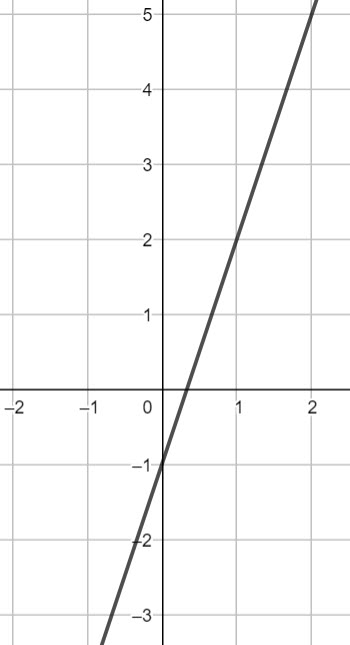
Which of the following is the correct equation of the following straight line
gradient = 3
y intercept = -1
Which of the following lines passes through the point (2 , 1)
Which of the following lines is parallel to \(y = \frac{1}{2}x+2\)
x - 2y + 3 = 0 can be rearranged into the form y = mx + c
x + 3 = 2y
\(y = \frac{1}{2}x+\frac{3}{2}\)
Which of he following gradients could represent the gradients of 2 perpendicular lines
A) 2
B) \(\frac{2}{5}\)
C) 5
D) \(-\frac{5}{2}\)
If a line has gradient m \(\frac{-1}{m}\)
What is the gradient of the line that is perpendicular to the line below
The gradient a line perpendicular to \(y = -\frac{2}{3}x-2\) can be written in the form \(\frac{a}{b}\)
Find a b
If a line has gradient m \(\frac{-1}{m}\)
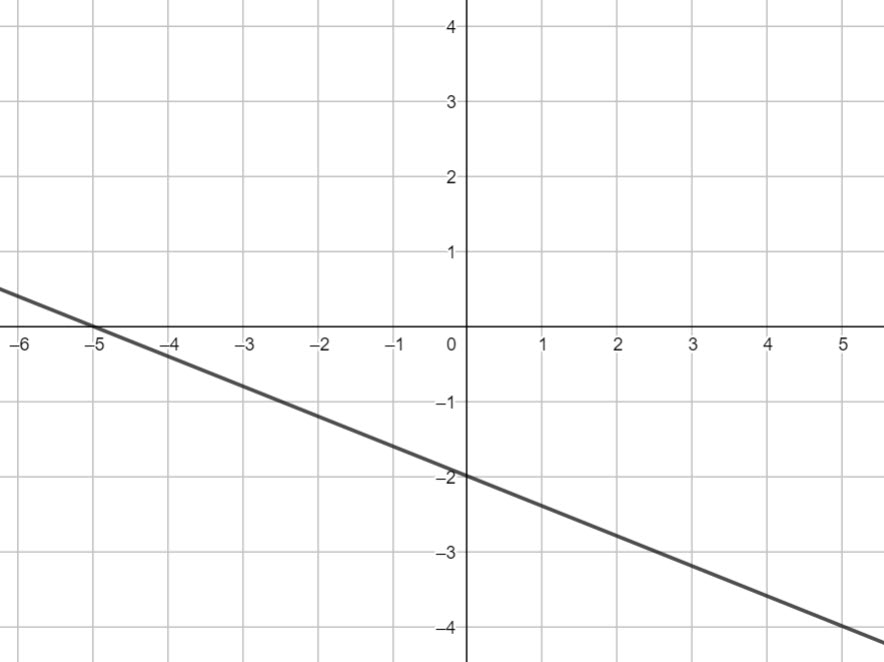
The equation line below can be written in the form \(ax+by+c=0\)
Find a b c
gradient = \(-\frac{2}{5}\)
y intercept = -2
\(y = -\frac{2}{5}x-2\\ 5y=-2x-10\\ 5y+2x+10=0\\ 2x+5y+10=0\)
The equation of the line that is perpendicular to the line below and that passes through the point (1,1) can be written in the form \(ax+2y+b=0\)
Find a b
gradient of line in graph = \(-\frac{2}{5}\)
gradient of perpendicular line = \(\frac{5}{2}\)
\(y = \frac{5}{2}x+c \)
passes through (1,1)
\(1 = \frac{5}{2}\cdot1+c\\ -\frac{3}{2} = c \\ y = \frac{5}{2}x-\frac{3}{2} \\ 2y=5x-3\\ -5x+2y+3=0 \)
Here is a quiz about parallel and perpendicular lines
Match up the gradients with the equations of the straight lines
y = m x + c , gradient = m
y = 2x + 1 , gradient = 2
2x + y + 1 = 0
y = -2x - 1 , gradient = -2
\(y-1= \frac{1}{2}(x+2)\) , gradient = 0.5
x + 2y - 1 = 0
y = -0.5x + 0.5 , gradient = -0.5
The equation of a line that is parallel to y = 3x - 2 and passes through the point (1 , 2) is given by
y = mx + c
Find m and c
If the line is parallel to y = 3x - 2 , then the gradient = 3
We can write it in the form
y = 3x + c
We know that it passes through (1 , 2)
2 = 3(1) + c
c = -1
Therefore, the equation is y = 3x - 1
The equation of a line that is parallel to \(y=\frac{2}{3}x+1\) and passes through (3 , -1) is given by
ax + by + d = 0 , where a > 0
Find a , b and d
If the line is parallel to \(y=\frac{2}{3}x+1\) , then the gradient = \(\frac{2}{3}\)
We can write it in the form
\(y=\frac{2}{3}x+c\)
We know that it passes through (3 , -1)
-1 = \(\frac{2}{3}\) (3) + c
c = -3
The equation is y = \(\frac{2}{3}\) x - 3
Multiply through by 3 and rearrange to put in the correct form:
3y = 2x - 9
2x - 3y - 9 = 0
The equation of the line \(l_1\) is given by 2x + 3y - 5 = 0
\(l_2\) is parallel to \(l_1\)
Which of the following could be the equation of the line \(l_2\)
2x + 3y - 5 = 0
\(y = -\frac{2}{3}x+\frac{5}{3}\)
Therefore the gradients of the lines \(l_1\) and \(l_2\) are \(-\frac{2}{3}\)
Rearrange 4x + 6y - 1 = 0 to find the gradient
\(y = -\frac{4}{6}x+\frac{1}{6}\)
The gradient of this line is \(-\frac{4}{6}=-\frac{2}{3}\)
A straight line, \(l\) \(\frac{1}{2}\)
What is the gradient of a line perpendicular to \(l\) ?
If the gradients of the lines are \(m_1\) and \(m_2\) , then \(m_1 \times m_2=-1\)
\(\frac{1}{2} \times m_2=-1\)
\(\frac{1}{2} \times (-2)=-1\)
The gradient of \(l_1\) is \(m_1\)
The gradient of \(l_2\) is \(m_2\)
What is \(m_1 \times m_2\)
Since these lines are perpendicular, then \(m_1 \times m_2=-1\)
What is the gradient of a line that is perpendicular to the one in the graph?
The gradient of the line in the graph is \(-\frac{2}{3}\)
The gradient of the perpendicular line = \(\frac{-1}{-\frac{2}{3}}=\frac{3}{2}\)
the equation of the line \(l_1\) is given by
y - 3 = -2 (x - 2)
\(l_2\) is perpendicular to \(l_1\)
What is the gradient of \(l_2\) ?
gradient of \(l_1\) = -2
gradient of \(l_2=-\frac{1}{-2}=\frac{1}{2}\)
The equation of the line \(l_1\) is given by 2x + 5y - 5 = 0
\(l_2\) is perpendicuar to \(l_1\)
Which of the following could be the equation of the line \(l_2\)
2x + 5y - 5 = 0
\(y = -\frac{2}{5}x+1\)
The gradient of the line \(l_1\) = \(-\frac{2}{5}\)
Therefore, the gradient of the line \(l_2\) = \(\frac{5}{2}\)
Rearrange 5x - 2y + 3 = 0 to find the gradient
2y = 5x + 3
\(y=\frac{5}{2}x+\frac{3}{2}\)
The gradient of this line is \(\frac{5}{2}\)
The lines \(l_1,l_2, l_3 \) and \( l_4\) form a square.
\( l_1:\) x + 2y = 12
\( l_2:\) 2x - y = -6
\( l_3: \ y=-\frac{1}{2}x+\frac{7}{2}\)
Which of the following lines completes the square?
gradient of \( l_1\) = \(-\frac{1}{2}\)
gradient of \( l_2\) = 2
gradient of \( l_3\) = \(-\frac{1}{2}\)
Therefore, gradient of \( l_4\) = 2
There are two possible solutions:
The line \(l_1\) has equation 2x+5y+6=0
The line \(l_2\) is perpendicular to the line \(l_1\) and passes through the point (2 , -2)
a) Find the equation of \(l_2\) in the form ax+by+d=0, where a, b and d are constants.
b) Find the coordinates where \(l_2\) meets the y axis
If the gradient of a line is m \({-1 \over m}\)
The point A has coordinates (a , 3) and the point B has coordinates (7 , b).
The line AB has equation 2x + 3y = 11.
a) Find the values of a and b
The line AC is perpendicular to the line AB.
b) Find the equation of the line AC in the form ax + by + d = 0, where a, b and d are constants
c) Given that C lies on the x axis, find its coordinates.
b) the line AC is perpendicular to AB and passes through the point A (found in part a)
The line \(l_1 \) passes through the point P(3k , 2k) with gradient = -2.
\(l_1 \) meets the x axis at A and the y axis at B.
a) Find the equation of the line \(l_1 \) and show that A(4k , 0)
b) Find the area of the triangle AOB in terms of k
The line \(l_2\) passes through P and is perpendicular to \(l_1 \)
c) Find the equation of \(l_2\)
\(l_2\) meets the x axis at C
d) Show that the midpoint of PC lies on the line y = x
The key to this type of question is to be able to visualize it.
Draw a sketch to help you:
Point A has coordinates (a b
The line 8x - 6y + 3 = 0 is the perpendicular bisector of AB.
Find a b
Find the gradient of AB in terms of a b
Gradient of AB is perpendicular to line 8x - 6y + 3 = 0
Find the midpoint of AB
Midpoint should lie on line 8x - 6y + 3 = 0
MY PROGRESS
Self-assessment How much of Equation of a Straight Line have you understood?
My notes
Which of the following best describes your feedback?











 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn