| Date | May 2016 | Marks available | 2 | Reference code | 16M.2.hl.TZ2.10 |
| Level | HL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 10 | Adapted from | N/A |
Question
A continuous random variable \(T\) has probability density function \(f\) defined by
\[f(t) = \left\{ {\begin{array}{*{20}{c}} {\frac{{t\left| {\sin 2t} \right|}}{\pi },}&{0 \leqslant t \leqslant \pi } \\ {0,}&{{\text{otherwise}}} \end{array}} \right.\]
Sketch the graph of \(y = f(t)\).
Use your sketch to find the mode of \(T\).
Find the mean of \(T\).
Find the variance of \(T\).
Find the probability that \(T\) lies between the mean and the mode.
(i) Find \(\int_0^\pi {f(t){\text{d}}t} \) where \(0 \leqslant T \leqslant \frac{\pi }{2}\).
(ii) Hence verify that the lower quartile of \(T\) is \(\frac{\pi }{2}\).
Markscheme
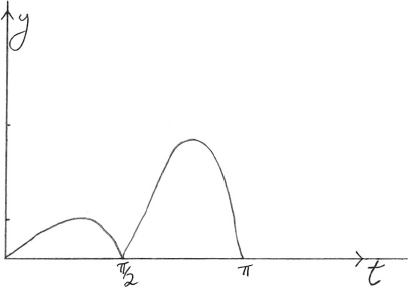
two enclosed regions (\(0 \leqslant t \leqslant \frac{\pi }{2}\) and \(\frac{\pi }{2} \leqslant t \leqslant \pi \)) bounded by the curve and the \(t\)-axis A1
correct non-symmetrical shape for \(0 \leqslant t \leqslant \frac{\pi }{2}\) and
\(\frac{\pi }{2} < {\text{mode of }}T < \pi {\text{ clearly apparent}}\) A1
[2 marks]
\({\text{mode}} = 2.46\) A1
[1 mark]
\({\text{E}}(T) = \frac{1}{\pi }\int_0^\pi {{t^2}\left| {\sin 2t} \right|{\text{d}}t} \) (M1)
\( = 2.04\) A1
[2 marks]
EITHER
\({\text{Var}}(T) = \int_0^\pi {(t - } 2.03788 \ldots {)^2}\left( {\frac{{t\left| {\sin 2t} \right|}}{\pi }} \right){\text{d}}t\) (M1)(A1)
OR
\({\text{Var}}(T) = \int_0^\pi {{t^2}} \left( {\frac{{t\left| {\sin 2t} \right|}}{\pi }} \right){\text{d}}t - {(2.03788 \ldots )^2}\)
(M1)(A1)
THEN
\({\text{Var}}(T) = 0.516\) A1
[3 marks]
\(\frac{1}{\pi }\int_{{\text{2.03788}} \ldots }^{{\text{2.456590}} \ldots } {t\left| {\sin 2t} \right|{\text{d}}t = {\text{0.285}}} \) (M1)A1
[2 marks]
(i) attempting integration by parts (M1)
\((u = t,{\text{ d}}u = {\text{d}}t,{\text{ d}}v = \sin 2t{\text{ d}}t\) and \(v = - \frac{1}{2}\cos 2t)\)
\(\frac{1}{\pi }\left[ {t\left( { - \frac{1}{2}\cos 2t} \right)} \right]_0^r - \frac{1}{\pi }\int_0^r {\left( { - \frac{1}{2}\cos 2t} \right){\text{d}}t} \) A1
Note: Award A1 if the limits are not included.
\( = \frac{{\sin 2T}}{{4\pi }} - \frac{{T\cos 2T}}{{2\pi }}\) A1
(ii) \(\frac{{\sin \pi }}{{4\pi }} - \frac{{\frac{\pi }{2}\cos \pi }}{{2\pi }} = \frac{1}{4}\) A1
as \({\text{P}}\left( {0 \leqslant T \leqslant \frac{\pi }{2}} \right) = \frac{1}{4}\) (or equivalent), then the lower quartile of \(T\) is \(\frac{\pi }{2}\) R1AG
[5 marks]
Examiners report
This question was generally accessible to the large majority of candidates. A substantial number of candidates were able to neatly and accurately sketch a non-symmetric bimodal continuous probability density function and to calculate its mean, mode and variance. Quite a few candidates unfortunately attempted this question with their GDC set in degrees.
This question was generally accessible to the large majority of candidates. A substantial number of candidates were able to neatly and accurately sketch a non-symmetric bimodal continuous probability density function and to calculate its mean, mode and variance. Quite a few candidates unfortunately attempted this question with their GDC set in degrees.
This question was generally accessible to the large majority of candidates. A substantial number of candidates were able to neatly and accurately sketch a non-symmetric bimodal continuous probability density function and to calculate its mean, mode and variance. Quite a few candidates unfortunately attempted this question with their GDC set in degrees.
This question was generally accessible to the large majority of candidates. A substantial number of candidates were able to neatly and accurately sketch a non-symmetric bimodal continuous probability density function and to calculate its mean, mode and variance. Quite a few candidates unfortunately attempted this question with their GDC set in degrees.
This question was generally accessible to the large majority of candidates. A substantial number of candidates were able to neatly and accurately sketch a non-symmetric bimodal continuous probability density function and to calculate its mean, mode and variance. Quite a few candidates unfortunately attempted this question with their GDC set in degrees.
This question was generally accessible to the large majority of candidates. A substantial number of candidates were able to neatly and accurately sketch a non-symmetric bimodal continuous probability density function and to calculate its mean, mode and variance. Quite a few candidates unfortunately attempted this question with their GDC set in degrees.

