| Date | November 2013 | Marks available | 6 | Reference code | 13N.1.hl.TZ0.2 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 2 | Adapted from | N/A |
Question
The discrete random variable X has probability distribution:
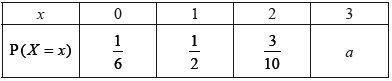
(a) Find the value of a.
(b) Find \({\text{E}}(X)\).
(c) Find \({\text{Var}}(X)\).
Markscheme
(a) \(\frac{1}{6} + \frac{1}{2} + \frac{3}{{10}} + a = 1 \Rightarrow a = \frac{1}{{30}}\) A1
(b) \({\text{E}}(X) = \frac{1}{2} + 2 \times \frac{3}{{10}} + 3 \times \frac{1}{{30}}\) M1
\(= \frac{6}{5}\) A1
Note: Do not award FT marks if a is outside [0, 1].
[2 marks]
(c) \({\text{E}}({X^2}) = \frac{1}{2} + {2^2} \times \frac{3}{{10}} + {3^2} \times \frac{1}{{30}} = 2\) (A1)
attempt to apply \({\text{Var}}(X) = {\text{E}}({X^2}) - {\left( {{\text{E}}(X)} \right)^2}\) M1
\(\left( { = 2 - \frac{{36}}{{25}}} \right) = \frac{{14}}{{25}}\) A1
[3 marks]
Total [6 marks]
Examiners report
This was very well answered and many fully correct solutions were seen. A small number of candidates made arithmetic mistakes in part a) and thus lost one or two accuracy marks. A few also seemed unaware of the formula \({\text{Var}}(X) = {\text{E}}({X^2}) - {\text{E}}{(X)^2}\) and resorted to seeking an alternative, sometimes even attempting to apply a clearly incorrect \({\text{Var}}(X) = \sum {{{({x_i} - \mu )}^2}} \).

