| Date | May 2016 | Marks available | 5 | Reference code | 16M.1.hl.TZ1.7 |
| Level | HL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 7 | Adapted from | N/A |
Question
Sketch on the same axes the curve \(y = \left| {\frac{7}{{x - 4}}} \right|\) and the line \(y = x + 2\), clearly indicating any axes intercepts and any asymptotes.
Find the exact solutions to the equation \(x + 2 = \left| {\frac{7}{{x - 4}}} \right|\).
Markscheme
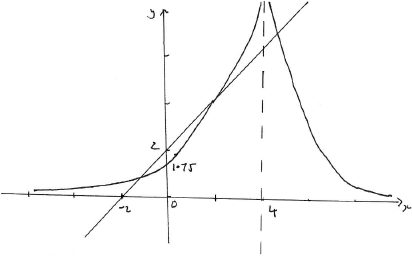
A1 for vertical asymptote and for the \(y\)-intercept \(\frac{7}{4}\)
A1 for general shape of \(y = \left| {\frac{7}{{x - 4}}} \right|\) including the \(x\)-axis as asymptote
A1 for straight line with \(y\)-intercept 2 and \(x\)-intercept of \( - 2\) A1A1A1
[3 marks]
METHOD 1
for \(x > 4\)
\((x + 2)(x - 4) = 7\) (M1)
\({x^2} - 2x - 8 = 7 \Rightarrow {x^2} - 2x - 15 = 0\)
\((x - 5)(x + 3) = 0\)
\(({\text{as }}x > 4{\text{ then}}){\text{ }}x = 5\) A1
Note: Award A0 if \(x = - 3\) is also given as a solution.
for \(x < 4\)
\((x + 2)(x - 4) = - 7\) M1
\( \Rightarrow {x^2} - 2x - 1 = 0\)
\(x = \frac{{2 \pm \sqrt {4 + 4} }}{2} = 1 \pm \sqrt 2 \) (M1)A1
Note: Second M1 is dependent on first M1.
[5 marks]
METHOD 2
\({(x + 2)^2} = \frac{{49}}{{{{(x - 4)}^2}}}\) M1
\({x^4} - 4{x^3} - 12{x^2} + 32x + 15 = 0\) A1
\((x + 3)(x - 5)({x^2} - 2x - 1) = 0\)
\(x = 5\) A1
Note: Award A0 if \(x = - 3\) is also given as a solution.
\(x = \frac{{2 \pm \sqrt {4 + 4} }}{2} = 1 \pm \sqrt 2 \) (M1)A1
[5 marks]
Examiners report
Though generally well done, some candidates lost marks unnecessarily by not heeding the instruction to clearly indicate the axes intercepts and asymptotes.
Though this was generally well done, quite a few of the candidates failed to use the graph drawn in part (a) to discount one of the solutions obtained in part (b).

