| Date | May 2016 | Marks available | 2 | Reference code | 16M.2.hl.TZ1.5 |
| Level | HL only | Paper | 2 | Time zone | TZ1 |
| Command term | Write down | Question number | 5 | Adapted from | N/A |
Question
The function \(f\) is given by \(f(x) = \frac{{3{x^2} + 10}}{{{x^{\text{2}}} - 4}},{\text{ }}x \in \mathbb{R},{\text{ }}x \ne 2,{\text{ }}x \ne - 2\).
Prove that \(f\) is an even function.
Sketch the graph \(y = f(x)\).
Write down the range of \(f\).
Markscheme
\(f( - x) = \frac{{3{{( - x)}^2} + 10}}{{{{( - x)}^2} - 4}}\) A1
\( = \frac{{3{x^2} + 10}}{{{x^2} - 4}} = f(x)\)
\(f(x) = f( - x)\) R1
hence this is an even function AG
Note: Award A1R1 for the statement, all the powers are even hence \(f(x) = f( - x)\).
Note: Just stating all the powers are even is A0R0.
Note: Do not accept arguments based on the symmetry of the graph.
[2 marks]
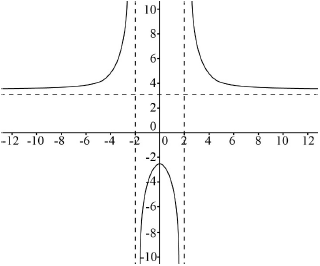
correct shape in 3 parts which are asymptotic and symmetrical A1
correct vertical asymptotes clear at 2 and –2 A1
correct horizontal asymptote clear at 3 A1
[3 marks]
\(f(x) > 3\) A1
\(f(x) \leqslant - 2.5\) A1
[2 marks]
Examiners report
Most candidates were able to prove that a function was even, although many attempted to show special cases, rather than a general proof. Many lost marks through not showing the asymptotes on their sketch. Marks were commonly lost in incorrect use of inequalities for the range of the function.
Most candidates were able to prove that a function was even, although many attempted to show special cases, rather than a general proof. Many lost marks through not showing the asymptotes on their sketch. Marks were commonly lost in incorrect use of inequalities for the range of the function.
Most candidates were able to prove that a function was even, although many attempted to show special cases, rather than a general proof. Many lost marks through not showing the asymptotes on their sketch. Marks were commonly lost in incorrect use of inequalities for the range of the function.

