| Date | May 2011 | Marks available | 7 | Reference code | 11M.2.sl.TZ2.10 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 10 | Adapted from | N/A |
Question
The diagram below shows a plan for a window in the shape of a trapezium.
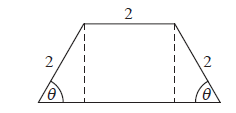
Three sides of the window are \(2{\text{ m}}\) long. The angle between the sloping sides of the window and the base is \(\theta \) , where \(0 < \theta < \frac{\pi }{2}\) .
Show that the area of the window is given by \(y = 4\sin \theta + 2\sin 2\theta \) .
Zoe wants a window to have an area of \(5{\text{ }}{{\text{m}}^2}\). Find the two possible values of \(\theta \) .
John wants two windows which have the same area A but different values of \(\theta \) .
Find all possible values for A .
Markscheme
evidence of finding height, h (A1)
e.g. \(\sin \theta = \frac{h}{2}\) , \(2\sin \theta \)
evidence of finding base of triangle, b (A1)
e.g. \(\cos \theta = \frac{b}{2}\) , \(2\cos \theta \)
attempt to substitute valid values into a formula for the area of the window (M1)
e.g. two triangles plus rectangle, trapezium area formula
correct expression (must be in terms of \(\theta \) ) A1
e.g. \(2\left( {\frac{1}{2} \times 2\cos \theta \times 2\sin \theta } \right) + 2 \times 2\sin \theta \) , \(\frac{1}{2}(2\sin \theta )(2 + 2 + 4\cos \theta )\)
attempt to replace \(2\sin \theta \cos \theta \) by \(\sin 2\theta \) M1
e.g. \(4\sin \theta + 2(2\sin \theta \cos \theta )\)
\(y = 4\sin \theta + 2\sin 2\theta \) AG N0
[5 marks]
correct equation A1
e.g. \(y = 5\) , \(4\sin \theta + 2\sin 2\theta = 5\)
evidence of attempt to solve (M1)
e.g. a sketch, \(4\sin \theta + 2\sin \theta - 5 = 0\)
\(\theta = 0.856\) \(({49.0^ \circ })\) , \(\theta = 1.25\) \(({71.4^ \circ })\) A1A1 N3
[4 marks]
recognition that lower area value occurs at \(\theta = \frac{\pi }{2}\) (M1)
finding value of area at \(\theta = \frac{\pi }{2}\) (M1)
e.g. \(4\sin \left( {\frac{\pi }{2}} \right) + 2\sin \left( {2 \times \frac{\pi }{2}} \right)\) , draw square
\(A = 4\) (A1)
recognition that maximum value of y is needed (M1)
\(A = 5.19615 \ldots \) (A1)
\(4 < A < 5.20\) (accept \(4 < A < 5.19\) ) A2 N5
[7 marks]
Examiners report
As the final question of the paper, this question was understandably challenging for the majority of the candidates. Part (a) was generally attempted, but often with a lack of method or correct reasoning. Many candidates had difficulty presenting their ideas in a clear and organized manner. Some tried a "working backwards" approach, earning no marks.
In part (b), most candidates understood what was required and set up an equation, but many did not make use of the GDC and instead attempted to solve this equation algebraically which did not result in the correct solution. A common error was finding a second solution outside the domain.
A pleasing number of stronger candidates made progress on part (c), recognizing the need for the end point of the domain and/or the maximum value of the area function (found graphically, analytically, or on occasion, geometrically). However, it was evident from candidate work and teacher comments that some candidates did not understand the wording of the question. This has been taken into consideration for future paper writing.

