| Date | November 2017 | Marks available | 7 | Reference code | 17N.1.sl.TZ0.6 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 6 | Adapted from | N/A |
Question
Let \(f(x) = 15 - {x^2}\), for \(x \in \mathbb{R}\). The following diagram shows part of the graph of \(f\) and the rectangle OABC, where A is on the negative \(x\)-axis, B is on the graph of \(f\), and C is on the \(y\)-axis.
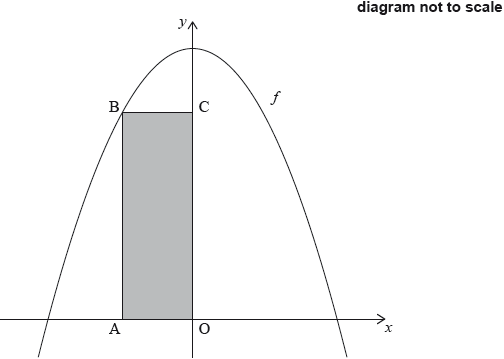
Find the \(x\)-coordinate of A that gives the maximum area of OABC.
Markscheme
attempt to find the area of OABC (M1)
eg\(\,\,\,\,\,\)\({\text{OA}} \times {\text{OC, }}x \times f(x),{\text{ }}f(x) \times ( - x)\)
correct expression for area in one variable (A1)
eg\(\,\,\,\,\,\)\({\text{area}} = x(15 - {x^2}),{\text{ }}15x - {x^3},{\text{ }}{x^3} - 15x\)
valid approach to find maximum area (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\(A’(x) = 0\)
correct derivative A1
eg\(\,\,\,\,\,\)\(15 - 3{x^2},{\text{ }}(15 - {x^2}) + x( - 2x) = 0,{\text{ }} - 15 + 3{x^2}\)
correct working (A1)
eg\(\,\,\,\,\,\)\(15 = 3{x^2},{\text{ }}{x^2} = 5,{\text{ }}x = \sqrt 5 \)
\(x = - \sqrt 5 {\text{ }}\left( {{\text{accept A}}\left( { - \sqrt 5 ,{\text{ }}0} \right)} \right)\) A2 N3
[7 marks]

