| Date | May 2011 | Marks available | 7 | Reference code | 11M.1.sl.TZ1.6 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Solve | Question number | 6 | Adapted from | N/A |
Question
Solve the equation \(2\cos x = \sin 2x\) , for \(0 \le x \le 3\pi \) .
Markscheme
METHOD 1
using double-angle identity (seen anywhere) A1
e.g. \(\sin 2x = 2\sin x\cos x\) , \(2\cos x = 2\sin x\cos x\)
evidence of valid attempt to solve equation (M1)
e.g. \(0 = 2\sin x\cos x - 2\cos x\) , \(2\cos x(1 - \sin x) = 0\)
\(\cos x = 0\) , \(\sin x = 1\) A1A1
\(x = \frac{\pi }{2}\) , \(x = \frac{{3\pi }}{2}\) , \(x = \frac{{5\pi }}{2}\) A1A1A1 N4
METHOD 2
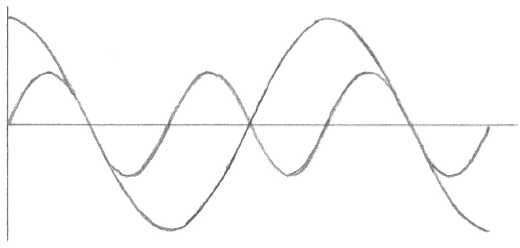 A1A1M1A1
A1A1M1A1
Notes: Award A1 for sketch of \(\sin 2x\) , A1 for a sketch of \(2\cos x\) , M1 for at least one intersection point seen, and A1 for 3 approximately correct intersection points. Accept sketches drawn outside \(\left[ {0,3\pi } \right]\) , even those with more than 3 intersections.
\(x = \frac{\pi }{2}\) , \(x = \frac{{3\pi }}{2}\) , \(x = \frac{{5\pi }}{2}\) A1A1A1 N4
[7 marks]
Examiners report
By far the most common error was to “cancel” the \(\cos x\) and find only two of the three solutions. It was disappointing how few candidates solved this by setting factors equal to zero. Some candidates wrote all three answers from \(\sin x = 1\) , which only earned two of the three final marks. On a brighter note, many candidates found the \(\frac{{5\pi }}{2}\) , which showed an appreciation for the period of the function as well as the domain restriction. A handful of candidates cleverly sketched both graphs and used the intersections to find the three solutions.

